基于农田肥力算法的函数寻优算法

一、理论基础

1、农田肥力算法

本文从自然界农田的肥力出发，提出了一种新的元启发式算法——农田肥力算法(Farmland fertility algorithm, FFA)，该算法将农田分成若干部分，并在内部存储和外部存储中以两种类型的最优效率对每个部分的解进行优化。
在介绍了农田肥力算法的基础上，用公式对算法的各个阶段和关键点进行了逐步的说明。该算法一般由6个阶段组成，图1的流程图显示了农田肥力算法的关键阶段，关键点完整地显示在6个步骤中。

1.1 第一阶段：初始值

在这一阶段，种群的产生是根据农田的部分数量和每个部分可用解决方案的数量进行的。以式(1)的形式表示初始种群的数量：$$N=k\ast n\text{\hspace{1em}(1)}$$其中，$N$表示搜索空间中的种群总数，$k$确定优化问题的每一部分的数量。根据优化问题，可以确定农田的标准剖面数。因此，整个搜索空间被划分为$k$个部分，每个部分都有特定数量的解决方案$n$表示每个部分农田中现有解决方案的数量，此数字是可变的整数。事实上，搜索空间的每个部分都有很多可用的解决方案。式(2)表示搜索空间中种群位置的随机生成：$$x_{ij}=L_j+rand(0,1)\times (U_j-L_j)\text{\hspace{1em}(2)}$$其中，$U_j$和$L_j$分别是变量$x$的上界和下界，$rand$是$(0,1)$范围内的随机数，$j=[1,\cdots ,D]$表示$x$的各个维度，$i=[1,\cdots ,N]$。在此阶段，根据目标函数对整个搜索空间中的可用解进行评估。不考虑农田的数量，这一阶段是在整个搜索空间中对所有现有解决方案进行的。

1.1.1 确定$K$值

由文献[1]的描述可知：提出的算法是将搜索空间划分为$k$段，因此$k$值的确定是敏感的，通过5个假设证明了$k$值是$2\le k\le 8$。

1.2 第二阶段：确定农田各部分的土壤质量

通过式(3)和式(4)确定了每个农田部分(搜索空间部分)的质量。各部分农田的质量由各部分农田中现有解决方案的平均值得出。 S e c t i o n s = x ( a j ) , a = n ∗ ( s − 1 ) : n ∗ s s = { 1 , 2 , ⋯ , k } , j = { 1 , 2 , 3 , 4 } (3) Section_s=x(aj),\,\,a=n*(s-1):\,\,n*ss=\{1,2,\cdots,k\},\,\,j=\{1,2,3,4\}\tag{3} Sections​=x(aj),a=n∗(s−1):n∗ss={1,2,⋯,k},j={1,2,3,4}(3)式(3)简单地将每个部分中的可用解决方案分开。所以，我们可以分别计算每部分的平均值。根据式(3)，$x$等于搜索空间中的所有解，$s$表示截面数，$j＝[1,\cdots ,D]$表示变量$x$的维度。 F i t _ S e c t i o n s = M e a n ( allFit ( x j i ) i n S e c t i o n s ) , s = { 1 , 2 , ⋯ , k } , i = { 1 , 2 , ⋯ , n } (4) Fit\_Section_s=Mean(\text{allFit}(x_{ji})\,\,in\,\,Section_s),\,s=\{1,2,\cdots,k\},\,i=\{1,2,\cdots,n\}\tag{4} Fit_Sections​=Mean(allFit(xji​)inSections​),s={1,2,⋯,k},i={1,2,⋯,n}(4)其中，$Fit\_Section$定义了每一部分农田的质量，即每一部分都有的特定的质量，在搜索空间中是每一部分中所有可行解的平均适应度。因此，对于农田的每一个部分，计算出任何部分内的解的总平均值，最后，将其保存在合适的部分中。在这一阶段，农田肥力取决于每个部分及其解决方案和每个部分的平均值。

1.3 第三阶段：更新记忆

在确定每一块农田的解和每一块农田的平均值之后，我们更新每一块农田的局部内存和全局内存。每个部分的一些最佳情况存储在局部存储器中，所有部分的最佳情况存储在全局存储器中，局部存储器由根据式(5)确定，全局存储器根据式(6)确定。$$M_{local}=round(t\ast n)0.1<t<1\text{\hspace{1em}(5)}$$$$M_{Global}=round(t\ast N)0.1<t<1\text{\hspace{1em}(6)}$$其中，$M_{Global}$表示全局内存中的解决方案数量，$M_{local}$表示局部内存中的解决方案数量，解决方案根据这些内存中的大小和适用性进行放置，并在此阶段更新两个内存。更新内存后，确定最坏和最好的部分，算法进入下一阶段。

1.4 第四阶段：改变农田各部分的土壤质量

在这个阶段，在通过式(4)确定每个截面的质量后，质量最差的截面将有最大的变化。通过式(4)确定每个部分的质量。就质量而言，农田中最差的部分是一个问题，因此根据式(7)和式(8)将农田中最差部分中的所有现有解决方案与全局内存中的一个可用解决方案相结合。$$h=\alpha \ast rand(-1,1)\text{\hspace{1em}(7)}$$$$Xnew=h\ast (X_{ij}-X_{MGlobal})+X_{ij}\text{\hspace{1em}(8)}$$在式(8)中，$X_{MGlobal}$是全局内存中现有解中的一个随机解，而$\alpha$是一个介于0和1之间的数字，应该在计算开始时对其进行估值。$X_{ij}$是选择应用变化的农田最差部分的解决方案，$h$是根据式(7)可以计算的十进制数。因此，$Xnew$作为一种新的解决方案是通过应用更改获得的。在对农田最差部分进行更改后，其他部分应与整个搜索空间中的可用解决方案相结合，其他部分的可行解由式(9)和式(10)确定。$$h=\beta \ast rand(0,1)\text{\hspace{1em}(9)}$$$$Xnew=h\ast (X_{ij}-X_{uj})+X_{ij}\text{\hspace{1em}(10)}$$其中，$X_{uj}$是整个搜索空间中现有解中的随机解，$\beta$是一个介于0和1之间的数字，$X_{ij}$是一个与选择应用更改的部分(最差部分除外)相关的解决方案，$h$是一个十进制数，可根据式(9)计算。因此，$Xnew$作为一种新的解决方案，是通过应用更改获得的。

1.5 第五阶段：土壤组合

在这一阶段，农民在最后一阶段根据其本地记忆中的最佳可行解($Bes{t}_{Local}$)决定将农田各部分中的每种土壤组合起来。因此，并非所有可用的解决方案都与所有部分中的本地内存相结合，在此阶段，所有位置中的一些可用解决方案与有史以来最好的解决方案($Bes{t}_{Global}$)相结合，以提高每个部分中现有解决方案的质量。所考虑的解决方案与最佳全局或最佳局部的组合由式(11)确定。$$H=\{\begin{array}{l}{X}_{new}=X_{ij}+{\omega }_1\ast (X_{ij}-Bes{t}_{Global}(b))Q>rand\\ X_{new}=X_{ij}+rand(0,1)\ast (X_{ij}-Bes{t}_{Local}(b))else\end{array}\text{\hspace{1em}(11)}$$其中，$Q$是一个介于0和1之间的参数，必须在算法开始时确定。该参数确定了最佳全局($Bes{t}_{Global}$)解的组合量，${\omega }_1$作为农田肥力的参数，是一个整数，应在算法开始时确定，其数量根据算法的迭代逐渐减少(式(12)；$X_{ij}$是一种从所有部分中选择应用更改的解决方案。因此，$X_{new}$是一种新的解决方案，它是根据应用的更改实现的。$${\omega }_1={\omega }_1\ast R_{\nu }0<R_{\nu }<1\text{\hspace{1em}(12)}$$

1.6 第六阶段：终止条件

在此阶段，根据目标函数对整个搜索空间中的现有解进行评估。因此，在搜索空间中确定每个现有解决方案的适应度。在农田肥力结束时，对终止条件进行调查。如果我们达到了终止条件，算法就结束了；否则，算法将继续工作以确定达到终止条件。

2、FFA算法流程图

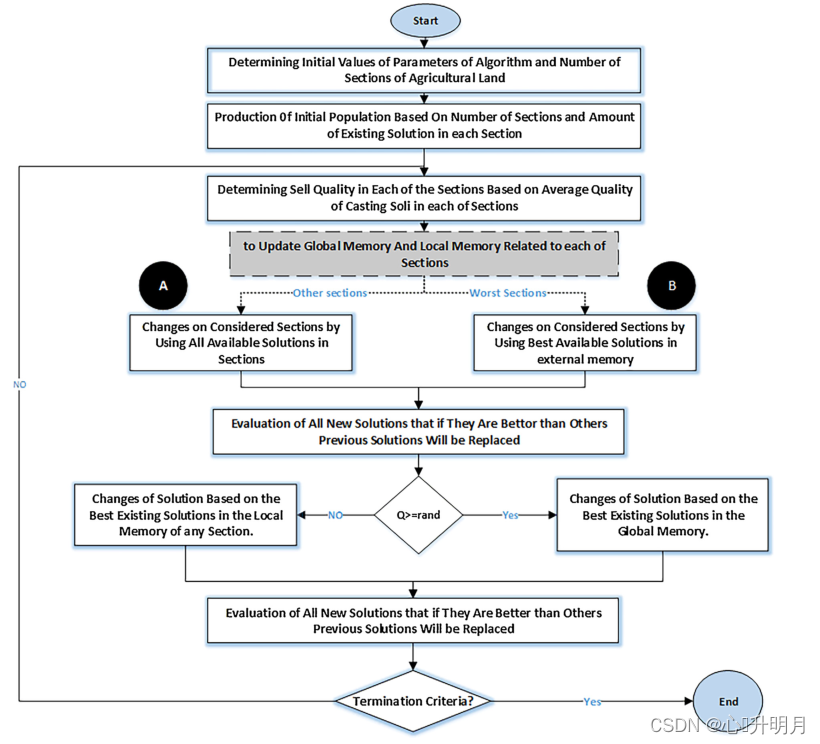
二、仿真实验与分析

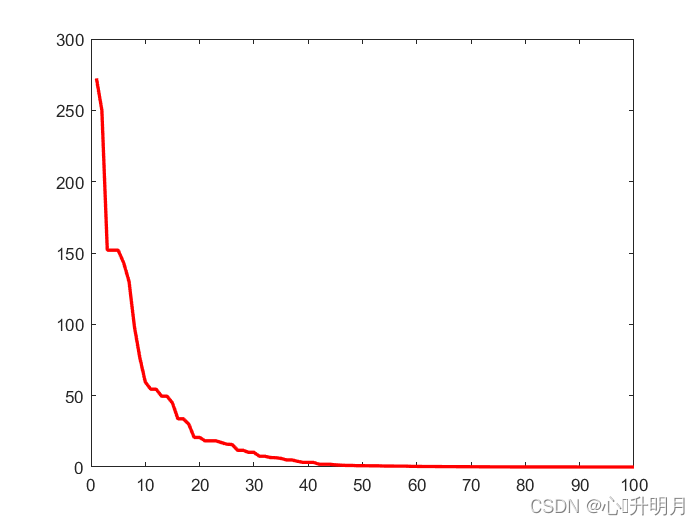
三、参考文献

[1] Human Shayanfar, Farhad Soleimanian Gharehchopogh. Farmland fertility: A new metaheuristic algorithm for solving continuous optimization problems[J]. Applied Soft Computing, 2017, 71: 728-746.