数据在计算机中的存储——数值数据的表示方法以及原码补码等系列深究

本文主要是介绍数据在计算机中的存储——数值数据的表示方法以及原码补码等系列深究，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

前言

数值在计算机中的表示方法这一块一直有些混乱，以此文深究记录保持记忆。
我们都知道，在计算机中数据的小数点并不是用某个二进制数字来表示的，而是用隐含的小数点的位置来表示的。根据小数点位置是否固定，将计算机中的数据表示格式分为两种，即定点格式和浮点格式。

---

一、定点数的表示方法

定点数指小数点在数中位置固定不变的数。定点数分为定点整数和定点小数，由于小数点位置固定不变，所以存储时小数点不进行存储，按照约定的位置计算数值。原理上讲，小数点的位置可以位于任何位置，但通常将定点数表示成纯小数或纯整数。

假设以机器字长n位表示定点数，从右至左，从高位到低位分别为x0，x1，x2…xn-1，xn，其中x0取值0和1分别表示正号和负号。如此，对于任意一个定点数x=xnxn-1…x2x1，在定点机器中可表示为：

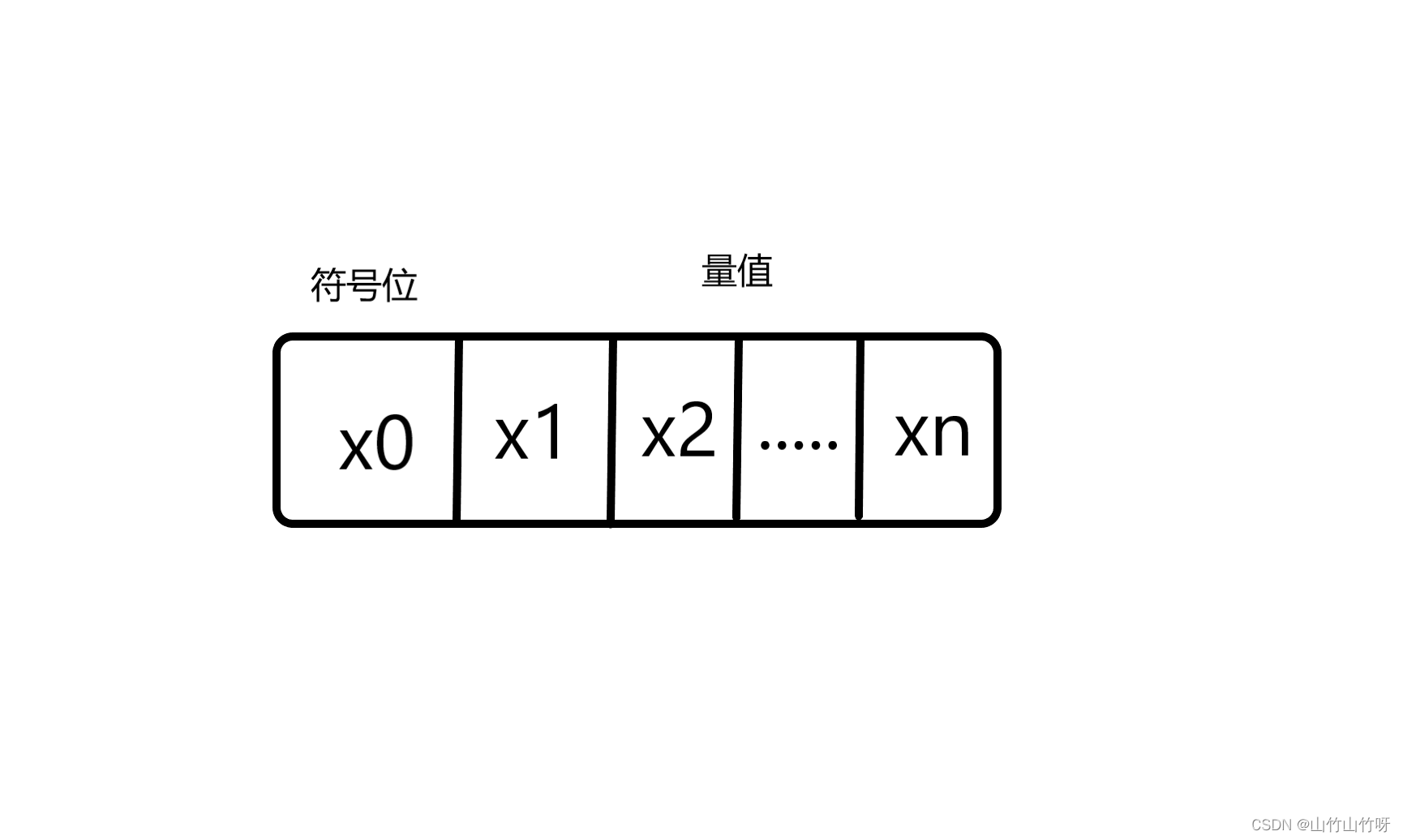
如果上图表示纯小数的话，那么小数点就在符号位x0和值位x1中间。
如果表示纯整数，那么小数点位于Xn的右边。

二、原码，反码与补码。

在学习之前，我们补习一些前置知识。

1.机器数

一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。那么，这里的 00000011 和 10000011 就是机器数。

2.真值

因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。
所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1

因此我的理解，机器数就是计算机用来存放数据时数据带有符号的二进制格式，而真值就是这个数的真实值。也就是将机器数的最高位符号位（0和1）变成符号。

好了，现在开始让我们正式学习原码，补码等变化规则：

1.原码

原码即真值

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

先给一个公式（这个公式不必要记住，用来理解真值与原码的转换）：

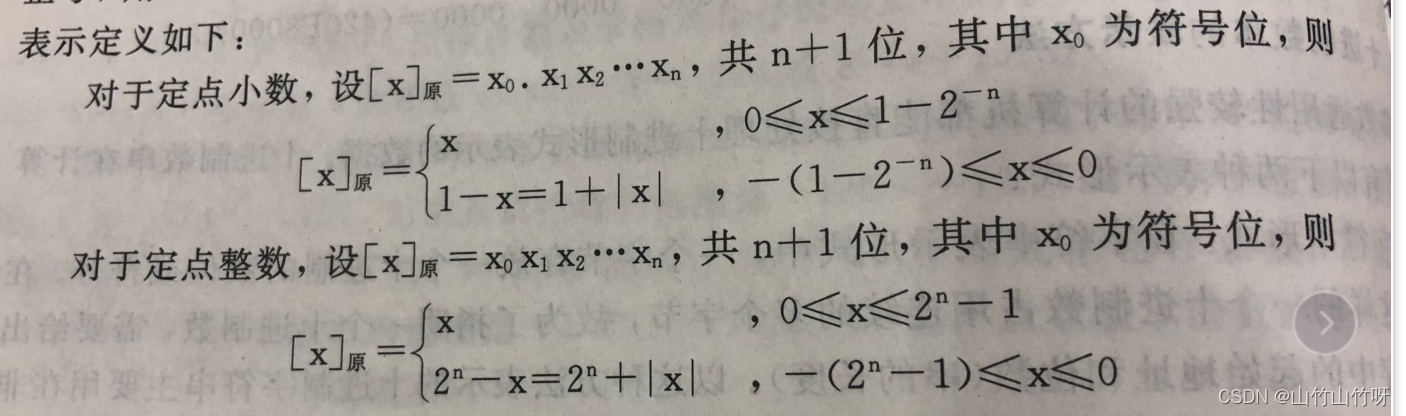
这里的x是真值，
我们用以上的公式代入做题：

x1= 0.1101  x2=-0.1010  x3=1001 x4=-1110
[x1]原=0.1101    [x2]原=1.1010
[x3]原=01001     [x4]原= 11110据观察所知：原码和真值之间就是将最高位的符号位变成了0和1， 其实换句话说，原码等于真值在最高位加上符号位。
我们再来对这个公式剖析，我们计算得知，这个公式对于正数其直接是[x]原=x; 
对于负数:如果是小数，就在其最高位+1，也就是[x]原=1-x,这里的x是负数，所以也就是 1+x，利用此结果将符号转换为1；
如果是负整数，直接在其最高为+1，也就是给真值取掉符号位之后加上2的n次方。  
负整数： -000 0001  取掉符号位  然后加上2的7次方， 也就等于 1000 0001  成功换算为原码。

2.反码

反码的表示方法是:

正数的反码是其本身负数的反码是在其原码的基础上, 符号位不变，其余各个位取反例：[+1] = [00000001]原 = [00000001]反[-1] = [10000001]原 = [11111110]反

3.补码

补码的表示方法是:

正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
例：
[+1] = [00000001]原 = [00000001]反 = [00000001]补[-1] = [10000001]原 = [11111110]反 = [11111111]补

扩展（关于原码补码等深究）

三、浮点数的表示方法

在科学计算中，常常会遇到非常大或非常小的数值，如果用定点数来表示的话，很难同时满足数据的表示范围和运算精度的要求。为了解决这一问题，计算机中采用了浮点数格式。所谓浮点数格式，是指在表示数据时，将浮点数的范围和精度分别表示。

在上述浮点数的表示格式中，阶符占1位，阶码值占m位，数符占1位，尾数值占n位。
后来为了便于软件移植，IEEE754规定了浮点数的表示标准，也定义了单精度（32位浮点数），双精度（64位浮点数）常规格式，如下图

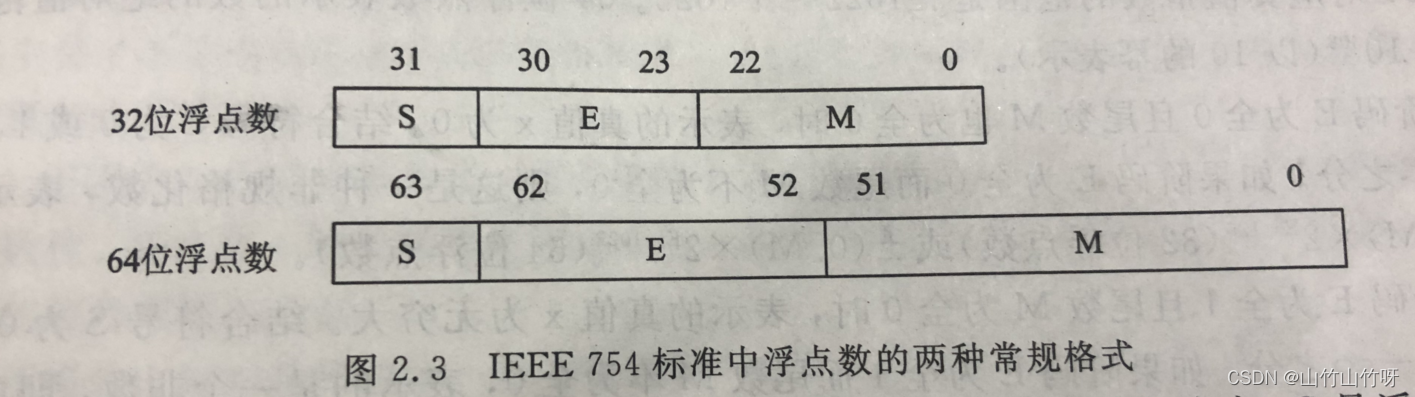
32位浮点数和64为浮点数中阶码的基数都是2.32位浮点数格式中，s是浮点数的的符号位，占1位，s=0表示正数，s=1表示负数，M是浮点数的尾数，放在低位部分，占23位，小数点放在浮点数的E和M之间，即M的最前面，实际尾数的取值为1.M;E是浮点数的阶码，占8位，阶符采用隐含方式。

浮点数的规格化：（正菜）
为了使浮点数格式统一，又尽可能提高其精度，通常采用浮点数规格化形式。

在IEEE754标准中，一个规格化的32位浮点数x的真值可表示为：

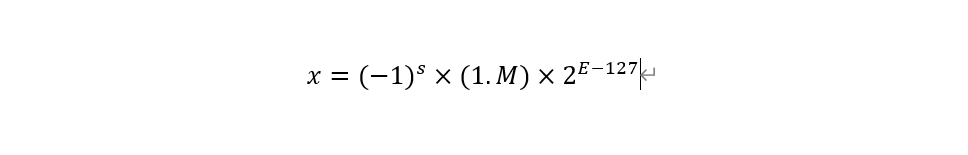
其中,S,M,E分别为32位浮点数表示格式和存储格式中的数符，尾数，公式中的E-127表示浮点数x的指数e，即e=E-127 或E=e+127。

在计算机中存储格式为16进制数（C2540000），其真值为：
先把存储格式表示为32位二进制数，

然后根据上图得出S=1 E=10000100 M=10101
代入公式（规格化公式）得：x=-110101=（-53)(10进制）;
例题：

我们求出上面的二进制数（-10101）=十进制数（-53)在计算机中的存储格式。
将其二进制数表示为浮点数形式，并使其尾数为1.M的形式。
110101=1.10101X2^5;
由上可知 S=1；E=5+127=132=10000100； M=1010 1000 0000 0000
可得存储格式的二进制数为：
1100 0101 0100 0000 0000 0000 0000
转换为十六进制（C2540000）

以上就是浮点数规格化存储的转换。

---

总结

繁杂的小知识,乱而要精。

这篇关于数据在计算机中的存储——数值数据的表示方法以及原码补码等系列深究的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---