Leetcode算法刷题练习笔记 美区国区（按难度题目整理）

也囊括非Leetcode的题目，如codality等，放在leetcode Hard之后

难度：EASY 简单

回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。例如，121 是回文，而 123 不是。

#include<string>class Solution {
public:bool isPalindrome(int x) {if(x<0)return false;string x_s=to_string(x);int i=x_s.length()-1;int n=i+1;while(i>=0){if(x_s[i]!=x_s[n-1-i])return false;i--;}return true;}
};

注意用string类的其他格式转换成string的函数是to_string()，而不是string()或者itos()

1. Two Sum 哈希表

美区链接
Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.
题目要求：找出数组中和为target的一对数，返回这对数的下标
解法方案：

• $O(n^2)$：暴力遍历法
• $O(nlogn)$：先排序，再二叉查找（最容易思考到，但是C++代码要返回下标就很费事）
• $O(n)$：用哈希表实现，C++用STL的unordered_map，python用list

$O(nlogn)$解法：
C++的二叉查找用STL的lower_bound(begin(),end(),val)，返回第一个大于等于val的元素的迭代器

vector<int> twoSum1(vector<int>& nums, int target) 
{int n = nums.size();vector<int>nums_copy = nums;sort(nums.begin(), nums.end());//先排序int i, num1, num2;for (i = 0; i < n - 1; i++){num1 = i;num2 = lower_bound(nums.begin() + i + 1, nums.end(), target - nums[i])- nums.begin();//将迭代器转换成int的方法 注意.end()对应int是n而不是n-1if (num2 != -1&&num2!=n && nums[num2] == target - nums[num1])break;}//得到元素后找出下标int k1 = -1, k2 = -1,j;for (i = 0; i < n; i++){if (nums_copy[i] == nums[num1]){k1 = i; break;}}for (i = 0; i < n; i++) {if (nums_copy[i] == nums[num2]&&i!=k1) { k2 = i; break; }}if (k1 == -1 || k2 == -1)return {};		vector<int>res;res.push_back(k1);res.push_back(k2);return res;
}

$O(n)$解法：
用哈希表unordered_map

vector<int> twoSum2(vector<int>& nums, int target)
{unordered_map<int, int> hashTable;  //建立从int（元素值）到int（元素下标）的哈希映射int i,j;for (i = 0; i < nums.size(); i++)hashTable[nums[i]] = i;for (i = 0; i < nums.size(); i++){j = hashTable[target - nums[i]];if (nums[i] + nums[j] == target && i != j)break;}vector<int>res;res.push_back(i);res.push_back(j);return res;
}

等价于官方python解法：（Two-pass Hash 两次哈希）

class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:hashmap = {}for i in range(len(nums)):hashmap[nums[i]] = ifor i in range(len(nums)):complement = target - nums[i]if complement in hashmap and hashmap[complement] != i:return [i, hashmap[complement]] 

事实上我怀疑if complement in hashmap 的判断会使得这个python解法时间复杂度上升到 $O(nlogn)$而不是官方说的$O(n)$，但是easy题目 $O(n^2)$都能过，这就也不重要了。

更简洁的方法是One-pass Hash 一次哈希，边建立hash表边查找，只用一个for循环，插入元素前先检验该元素是不是已经在哈希表中（因为有可能$nu{m}_1=nu{m}_2=\frac{target}{2}$）。

vector<int> twoSum2(vector<int>& nums, int target)
{unordered_map<int, int> hashTable;  //建立从int（元素值）到int（元素下标）的哈希映射int i,j;		for (i = 0; i < nums.size(); i++){j = hashTable[target - nums[i]];if (nums[i] + nums[j] == target && i != j)break;hashTable[nums[i]] = i;//插入操作挪到循环体中最后一步执行}vector<int>res;res.push_back(i);res.push_back(j);return res;
}

难度：Medium 中等

两数相加

将链表表示的两个非负整数相加，结果也以链表形式返回
https://leetcode-cn.com/problems/add-two-numbers/

不完备的题解 解决不了数据溢出

通过样例1565 / 1568

直接模拟人工计算时的相加过程，提取出两个链表表示的整数，再相加，变回链表，但是A/B链表长度一旦很长，超过unsigend long long表示范围的话就gg了
注意：queue的用法，判空empty()，队头元素是q.front()

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {queue<int> list_1;queue<int> list_2;ListNode* p1=l1;ListNode* p2=l2;while(p1!=nullptr)      //store data in lists{list_1.push(p1->val);p1=p1->next;}while(p2!=nullptr){list_2.push(p2->val);p2=p2->next;}unsigned long long num1=0,num2=0,i=0;      //calculate value of listswhile(list_1.empty()!=1){num1+=list_1.front()*pow(10,i);list_1.pop();i++;}i=0;while(list_2.empty()!=1){num2+=list_2.front()*pow(10,i);list_2.pop();i++;}unsigned  long long sum=num1+num2;queue<int>res;while(sum!=0){int n=sum%10;res.push(n);    //lower digit pushed first, to be poped firstsum=sum/10;}ListNode* p=new ListNode;ListNode* newlist=p;//save the list headwhile(res.empty()!=1){p->val=res.front();res.pop();if(res.empty()==1){break;}ListNode* q=new ListNode;q->val=0;q->next=nullptr;//initialize the next nodep->next=q;p=p->next;}return newlist;}
};

官方题解

不用转换格式（链表——>整数——>链表），直接边加变构造新的链表，每个节点填入的值是res=A+B+进位的个位，下一个结点的进位是res的十位
公式如下： $res=[\frac{A+B+Carry}{10}]$ 、 $Carr{y}_i=(A+B+Carr{y}_{i-1})\%10$

只要逐位边加边构造链表，就不存在数字过大溢出的问题了

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode *head = nullptr, *tail = nullptr;int carry = 0;while (l1 || l2) {int n1 = l1 ? l1->val: 0;int n2 = l2 ? l2->val: 0;int sum = n1 + n2 + carry;if (!head) {head = tail = new ListNode(sum % 10);} else {tail->next = new ListNode(sum % 10);tail = tail->next;}carry = sum / 10;if (l1) {l1 = l1->next;}if (l2) {l2 = l2->next;}}if (carry > 0) {tail->next = new ListNode(carry);}return head;}
};

8. String to Integer (atoi)

Implement the myAtoi(string s) function, which converts a string to a 32-bit signed integer (similar to C/C++'s atoi function).
题目要求：实现字符串string类型转换成int类型的函数
原题目地址
暴力枚举法即可

int myAtoi(string s)
{int sign = 1;bool signflag = 0;bool zeroflag = 0;//0表示有可能出现“前面的0”； 1则相反vector<int> st;for (int i = 0; i < s.size(); i++){if (signflag == 0 && s[i] == ' ')continue;else if (signflag == 0 && s[i] == '+')signflag = 1;else if (signflag == 0 && s[i] == '-')signflag = 1, sign = -1;else if (s[i] == '0')//检查是否为“前面的0 ” {if (zeroflag == 1){signflag = 1, st.push_back(0);}else signflag = 1;//跳过 }else if (s[i] > '0' && s[i] <= '9')signflag = zeroflag = 1, st.push_back(s[i] - 48);//注意ASCII转换elsebreak;//其他情况(出现字母etc)，直接跳出循环，输出已扫描到的合法部分}int n = 0;long long num = 0, sum = 0;//循环计次 while (!st.empty()){num = st.back();st.pop_back();num *= pow(10, n);sum += num;n++;if (n > 10)//防止数字过大，中途num溢出{if (sign == 1)return  pow(2, 31) - 1;else return-pow(2, 31);}}long long res = sign * sum;if (res > pow(2, 31) - 1)res = pow(2, 31) - 1;else if (res < -pow(2, 31))res = -pow(2, 31);return res;
}

877. Stone Game

题目：leetcode题目

不完备的解 贪心算法

起初考虑了贪心算法+模拟
但是贪心算法（每一次都最两边之一较大的值）不能保证得到最优解，只有部分问题（Kruskal/prim最小生成树等算法中等同于最优解）

bool stoneGame1(vector<int>& piles) {int n = piles.size();int sumA = 0, sumB = 0, i, j = n - 1, k = 0;vector<bool>flags(n);//record if a pile has been taken(1)for (i = 1; i <= n && j >= k; i++)//simiulate every turn{if (i % 2 == 1)//aliceif (piles[k] > piles[j]){sumA += piles[k]; k++;}else{sumA += piles[j]; j--;}elseif (piles[k] > piles[j]){sumB += piles[k]; k++;}else{sumB += piles[j]; j--;}int restSum = accumulate(piles.begin() + k, piles.begin() + j + 1, 0);if (sumA > sumB + restSum) return true;}return false;
}

经启发后的解 DP

构造动态规划就需要先构造递推方程，也就是先构造DP表项

• 首先，DP表项的角标必须等价于当前状态
• 其次，DP表项的取值必须能直接转换成解并输出
  进而，状态转移表项DP[i,j]就可以表示状态[i,j]下的最优解，成功构造DP后只需要迭代到目标DP表项，比如DP[0][n-1]然后输出即可
  目前就见过的算法题而言，DP表项的角标最多两个(i,j即可一一对应一个状态)，但在算法课上曾见到一道连续矩阵相乘最值的问题，涉及到三个角标

//动态规划 构造dp[i][j] 为面对piles[i~j]时当前玩家能拿到的分数最大值（max{石头总和}）
//由此看出构造DP表项的两大要素：
//1、精准指明当前状态(往往1~2个角标) 2、表项取值本身==当前最优解（像这样要输出bool的解则要准确取值，直接判T/F）
bool stoneGame(vector<int>& piles) {const int N = 501;int dp[N][N] = { 0 };int sum = accumulate(piles.begin(), piles.end(), 0);int n = piles.size();int i = 0, j = n - 1,k=1;for (k = 1; j >= i; k++){int last1=0, last2=0;if (i > 0)last1 = dp[i - 1][j];if (j < n - 1)last2 = dp[i][j + 1];if (last1 + piles[i] > last2 + piles[j]){dp[i][j] = last1 + piles[i];if (k % 2 == 1 && dp[i][j] > sum / 2)return true;i++;}else{dp[i][j] = last2 + piles[j];if (k % 2 == 1 && dp[i][j] > sum / 2)return true;j--;}}return false;
}

官方数学巧解 不具普适性

组合数学可以构造证明：先下手的A永远有必胜策略，可以将piles[i] (i=0, 2, 4, …)涂成黑色，将piles[i] (i=1, 3, 5, …)涂成红色，先出手的一方总可以保证只取一种颜色的堆直到结束，而两种颜色石头数量之和必然有一方大于另一方（因为总数是奇数，不存在平局），所以借由2元上色的方式构造证明了先手必赢。

    bool stoneGame(vector<int>& piles) {return true}

547. 省份数量

题目：leetcode国区——省份数量

个人解法：BFS遍历

牢记BFS特征：用栈存储一个节点所有的邻接点(包括自己)，先入栈后出栈，出栈时标记该点已经被访问

void bfs(vector<vector<int>>& isConnected, int start, vector<int>& flags)
{int i, j;int n = isConnected.size();vector<int>Neighbors;Neighbors.push_back(start);while (Neighbors.size() > 0){int newN = Neighbors.back();Neighbors.pop_back();flags[newN] = 1;for (j = 0; j < n; j++)if (isConnected[newN][j] && flags[j] == 0){Neighbors.push_back(j);}}
}int findCircleNum(vector<vector<int>>& isConnected) {int i, res = 0,j;int n = isConnected.size();vector<int> flags(n);for (i = 0; i < n; i++){if (flags[i] == 1)continue;bfs(isConnected,i,flags);res++;}return res;
}

个人解法2：DFS遍历

牢记DFS特征：递归，dfs()里调用dfs()
使用Python可以用语法糖扩大栈空间

void dfs(vector<vector<int>>& isConnected, int start, vector<int>&flags)
{int i;bool not_counted = 1;int n = isConnected.size();flags[start] = 1;for (i = 0; i < n; i++){if (isConnected[i][start] && flags[i] == 0){dfs(isConnected, i, flags);}}
}int findCircleNum(vector<vector<int>>& isConnected) {int i, res = 0, j;int n = isConnected.size();vector<int> flags(n);for (i = 0; i < n; i++){if (flags[i] == 1)continue;dfs(isConnected, i, flags);res++;}return res;}

简化此题：很多时候DFS写不出来总是因为dfs()的参数太多，容易想错：
实际只需要传入一个参数：被dfs()的端点本身，一般是int表示，如这里的int start

• 如果问题数据规模小：其他参数一律写成全局变量，一开始申请足够空间
• 如果问题数据规模大：dfs()用函数模声明和定义成主要函数(这里的findCircleNum）的嵌套定义的函数

function<type(args_type)>funcName=[](args)
{/*function body*/};    //别忘了分号

用function<T>定义的函数可以定义在其他函数里面或者外面，很适合定义dfs()！

5. 最长回文子串

题目：

要点

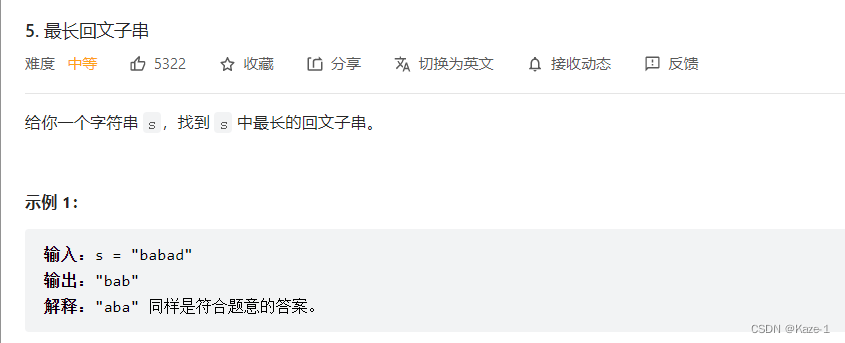
• 构造最优子结构
  
  进一步细化
  
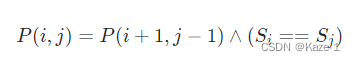
  边界条件是长度为1或2的字串：
  
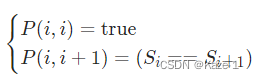
• 迭代填表的时候需要确保子问题的解已经计算出来（注意迭代顺序）
  外层约束是j，内层是i，确保子问题的解$dp[i+1][j-1]$在调用的时候已被计算完毕
  

6106. 统计无向图中无法互相到达点对数(连通分支问题)

题目：

本质上是找图的连通分支（由多少个连通的子图组成）

用DFS找出所有连通分支，统计每个连通分支的点数，所求两两组合数目res=res+新发现的连通分支点数$\times$之前所有(分支的)点数之和
牢记dfs()函数的写法：

• 如果问题数据规模小：其他参数一律写成全局变量，一开始申请足够空间
• 如果问题数据规模大：dfs()用函数模声明和定义成主要函数(这里的findCircleNum）的嵌套定义的函数
  dfs()的参数一般只需一个x就够

long long countPairs(int n, vector<vector<int>>& edges) {//转换数据结构vector<vector<int>>g(n);for (auto& e : edges){int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}vector<bool>visit(n);//int block = 0;   //统计连通分支的个数，但是用不上long long  prev = 0; //之前遇到的分支的点总和int count = 0;//每个分支内有多少点function<void(int)>dfs = [&](int x) //！函数内嵌套函数 (这样可以少开visit空间){if (visit[x] == 0){visit[x] = 1;count++;for (int p : g[x])//对于x的每一个邻接点执行dfsdfs(p);//block++;}};long long res = 0;for (int i = 0; i < n; i++){if (!visit[i]){count = 0;dfs(i);//进入dfs，算出这个分支区的countres += count * prev;//res+=新的分支点数*之前记录的所有点数prev += count;}}return res;
}

难度： HARD 困难

Median of Two Sorted Arrays

Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.

The overall run time complexity should be $O(log(m+n))$.

要求返回两个有序数组的中位数，并且时间复杂度控制在$O(log(m+n))$.
PS：当然，排序默认都是从小到大
用sort()函数不加参数都是从小到大排序

复杂度O(nlog(n))的解法

这个次优的解法很好想也很好实现，将两个数组合并后排序，再直接输出中位数就行

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {vector<int> nums;int i;for(i=0;i<nums1.size();i++)nums.push_back(nums1[i]);for(i=0;i<nums2.size();i++)nums.push_back(nums2[i]);sort(nums.begin(),nums.end());int n=nums.size();if(n%2==1)//odd elementsreturn nums[(n+1)/2-1];else return (nums[n/2-1]+nums[n/2])/2.;        }
};

最优题解

时间复杂度为O(log(n+m))
分治解法(Devide and Conquer)：

class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m=nums1.size();int n=nums2.size();int k1=(m+n+1)/2;int k2=(m+n+2)/2;return (getKth(nums1,nums2,0,0,k1)+getKth(nums1,nums2,0,0,k2))/2.;}#define MAX 0x7FFFFFFFdouble getKth(vector<int>& nums1, vector<int>& nums2,int start1,int start2,int k)//return the kth element of combined vector num1&num2//binary search+recursion{//one of them is vacantif(start1>=nums1.size())return nums2[start2+k-1];if(start2>=nums2.size())return nums1[start1+k-1];if(k==1)return min(nums1[start1],nums2[start2]);int m=nums1.size()-start1;int n=nums2.size()-start2;//get midval, the (k/2)th elementint midVal1,midVal2;if(m<k/2)midVal1=MAX;else midVal1=nums1[start1+k/2-1];if(n<k/2)midVal2=MAX;else midVal2=nums2[start2+k/2-1];//both of them has (k/2)th elementif(midVal1<midVal2)return getKth(nums1,nums2,start1+k/2,start2,k-k/2);elsereturn getKth(nums1,nums2,start1,start2+k/2,k-k/2);            }   
};

解题思路：



分而减枝：依照题目要求找中位数，可以化归于一个更普适的问题：找出两个有序数组合并后的第k个元素
如上所示，可以递归地分而减枝，每次传入两个数组各自的后半段(start1, start2来定位)和元素下标k。
分情况讨论：

• 有数组为空：返回另一个数组的[k-1]元素
• k==1:返回两段段首中较小的那个（因为较小者合并后排在前面，刚好是第一个）
• 非以上两种情况：对比两段中[k/2]元素，抛下[k/2]较小的那一段的前半段，在剩下部分中继续寻找第k-k/2个元素。
  原因：[k/2]较小意味着[k/2]在内的前半段必然在最终合并后排在第k个元素前面，所以可以抛下不管，在剩下的部分中继续寻找
  ~~~    注意：如果某段[k/2]元素不存在，那就将另一段前半段抛下（排在前面），因为用这样减枝方法留下来的段必然是较大的元素，而较小者才应该排到前面。
  程序实现时，将某段前半段抛下$\iff$将该段start加上k/2后递归调用

Stone Game IV

题目：leetcode Stone Game IV题目

题目要求：Alice 先行，输出Alice赢与否(bool)
每一步玩家可以移走面前石头中的i个（i是完全平方数1,4,9…），无法如此行动则输
重要隐含条件：玩家面前没有石头==输，因为玩家面前的石头数必然是自然数，只要存在石头就可以至少移走1个，从而不在这局输。

解法1 递归解法 DFS：

但是时间复杂度很高，官方解法是python+缓存存储
Python语法糖：@lru_cache(maxsize=none) 启用least-recently-used缓存存储模式，从而提高递归执行速度
这里用到一点计组的知识，cache的页替换策略包含很多种，替换策略汇总
相比传统的FIFO(先进先出)等方式，LRU策略使得代码执行速度更快

class Solution:def winnerSquareGame(self, n: int) -> bool:@lru_cache(maxsize=None)def dfs(remain):if remain == 0:return Falsesqrt_root = int(remain**0.5)for i in range(1, sqrt_root+1):# if there is any chance to make the opponent lose the game in the next round,#  then the current player will win.if not dfs(remain - i*i):return Truereturn Falsereturn dfs(n)

解法2 迭代解法 DP：

上述DFS的等价的迭代版本就是动态规划解法

    bool winnerSquareGame(int n){vector<int>dp(n+1);    //initially all zeros 注意一定是开n+1个空位for(int i=1;i<=n;i++){for(int k=1;k<=sqrt(i);k++)if(dp[i-k*k]==false){dp[i]=true;break;}}return dp[n];}

Codality 题目

codality麻烦的地方在于测试时只能看给出的三个样例，提交后（根据雇主设置）有可能看得到总体分数

demo task： MissingInteger

找没出现过的最小整数

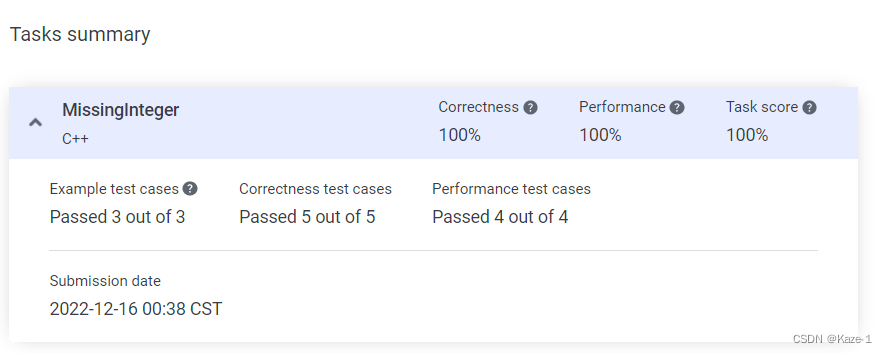
个人解法：全部100%完成度

O(nlogn)，先排序，排除1的特殊情形后从1的位置开始插空，找“空缺的最小整数”

#include<bits/stdc++.h>
using namespace std;int solution(vector<int> &A) {// write your code in [LANGVER]int n=A.size(),i;sort(A.begin(),A.end());int pivot=find(A.begin(),A.end(),1)-A.begin();//找出1的位置if(pivot==n)return 1; //如果没有1for(i=pivot+1;i<n;++i)if(A[i]-A[i-1]>1)return A[i-1]+1;return A[n-1]+1;
}

StackOverflow 哈希解法

int N = A.length;
Set<Integer> set = new HashSet<>();
for (int a : A) {if (a > 0) {set.add(a);}
}
for (int i = 1; i <= N + 1; i++) {if (!set.contains(i)) {return i;}
}

使用哈希表实现集合，在C++中的头文件是unordered_set
用到了一个引理：缺失的最小正整数必然落在$[1,N+1$]