《我的第一本算法书》阅读笔记 5-7 迪菲 - 赫尔曼密钥交换(Diffie-Hellman)

迪菲 - 赫尔曼（Diffie-Hellman）密钥交换是一种可以在通信双方之间安全交换密钥的方法。 这种方法通过将双方共有的秘密数值隐藏在公开数值相关的运算中，来实现双方之间密钥的安全交换。

在使用公式进行讲解之前，我们先通过图片来理解一下这个算法的概念

假设有一种方法可以合成两个密钥。使用这种 方法来合成密钥P和密 钥S，就会得到由这两 个密钥的成分所构成的密钥P-S。

这种合成方法有三个特征。第一，即使持有密钥P和合成的密钥P-S， 也无法把密钥S单独取 出来。

第二，不管是怎样合成而来的密钥，都可以把它作为新的元素，继续与别的密钥进行合成。比如上图 中的这个例子，使用密钥P和密钥P-S，还能合成出新的密钥P-P-S。

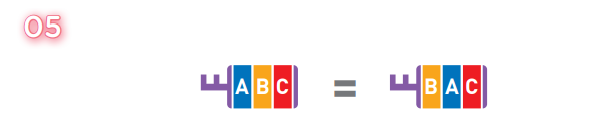
第三，密钥的合成结果与合成顺序无关，只与用了哪些密钥有关。比如合成密钥B和密钥C后，得到的是密 钥 B-C，再将其与密钥 A 合成，得到的就是密钥 A-B-C。而合成密钥 A 和密钥 C 后，得到的是密钥 A-C， 再将其与密钥B合成，得到的就是密钥B-A-C。此处的密钥A-B-C和密钥B-A-C是一样的。

我们试一试用这种方 法， 在A和B这两人之间安全地交换密钥吧。首先由A生成密钥P。

然后A把密钥P发送 给B。

接下来，A 和 B 各自准备自己的私有密钥SA 和SB。

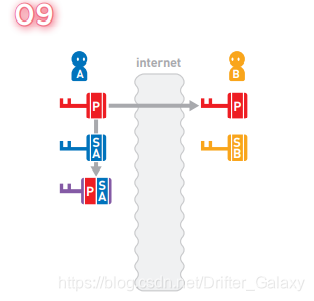
A利 用 密 钥P和 私 有 密 钥SA合 成 新 的 密 钥 P-SA。

B也利用密钥P和私有密钥SB合成新的密钥 P-SB。

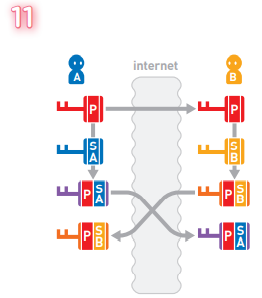
A将密钥P-SA 发送给 B，B 也将密钥 P-SB发送 给A。

A将私有密钥SA和收到的密钥P-SB合成为新 的密钥SA-P-SB。

同 样 地，B也 将 私 有 密钥SB和收到的密钥 P-SA合成为新的密钥 P-SA-SB。 于 是A和 B都得到了密钥P-SA-SB。这个密钥将作为 “加密密钥”和“解密密钥”来使用。

下面我们来验证该密 钥交换的安全性。因 为密钥P、密钥P-SA 和密钥P-SB需要在互 联网上进行传输，所 以有可能会被X窃听。

但 是，X无 法 用 自 己 窃听到的密钥合成出 P-SA-SB， 因 此 这 种 交换方式是安全的。

接下来用公式来表示这种密钥交换法。用P、G两个整数来表示一开始生成的公开密钥P。其中P是一 个非常大的素数，而G是素数P所对应的生成元（或者“原根”）中的一个。

首先，由 A 来准备素数P和生成元G。这两个数 公开也没有关系。

A将素数P和生成元G发送给B。

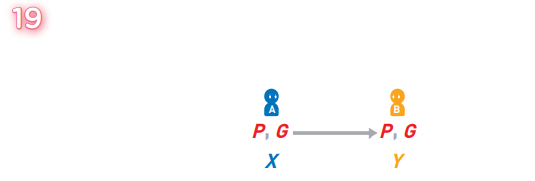
接下来，A和B分别准备了各自的秘密数字X和Y。X和Y都必须小于P-2

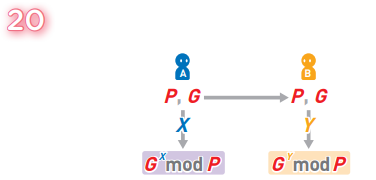
A 和 B 分别计算“（G的 秘 密 数 字 次 方 ）mod P”。mod 运算就是取余 运 算。“G mod P” 就 是计算G除以P后的余 数。此处的运算等同于 概念意义上的“合成”。

A和B将自己的计算结 果发送给对方。

A 和 B 收到对方的计算结果后，先计算这个值的秘密数字次方，然后再 mod P。最后A和B会得到相同 的结果。

下面来验证这种密钥交换法的安全性。即便X窃听了整个通信过程，也无法用窃听到的数字计算出A 和B共有的数字。而且，X也无法计算出保密数字X和Y。因此，此处使用迪菲-赫尔曼密钥交换是安 全的。

迪菲 - 赫尔曼密钥交换由惠特菲尔德·迪菲（Whitfield Diffie）和马丁·赫尔曼 （Martin Hellman）提出，两人在 2015 年获得了图灵奖。

根据素数 P、生成元 G 和“ mod P”求出 X 的问题就是“离散对数问题”，人们至今还未找到这个问题的解法，而迪菲 - 赫尔曼密钥交换正是利用了这个数学难题。(安全性基于离散对数难题)

使用迪菲 - 赫尔曼密钥交换，通信双方仅通过交换一些公开信息就可以实现密钥 交换。但实际上，双方并没有交换密钥，而是生成了密钥。因此，该方法又被叫作“迪菲 - 赫尔曼密钥协议”。

《我的第一本算法书》  [日]石田保辉 宫崎修一/著    张贝/译