5-9旅行售货员问题（回溯）

本文主要是介绍5-9旅行售货员问题（回溯），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

5-9旅行售货员问题（回溯）

一、问题描述

有n个城市，找从一城市出发走遍n个城市的最短回路问题。
在这里插入图片描述

二、分析

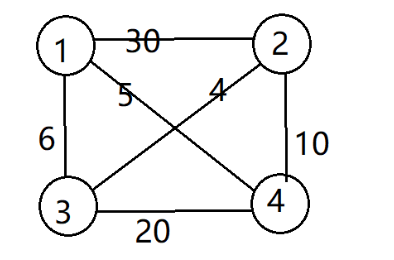
我们设起点为1，其他地点设为2，3，4…n。我们起初将所有路径费用都设置成∞，然后再输入相通路径的费用，再更新费用值。我们以下图为例。如下图：
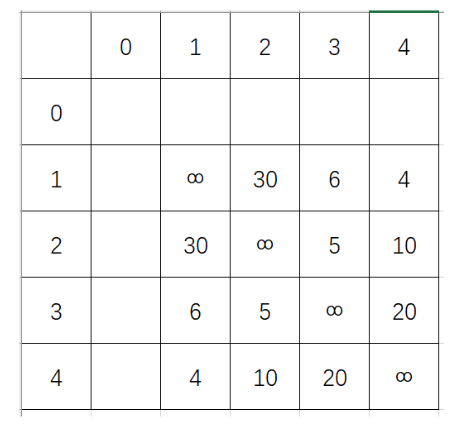
在这里插入图片描述
我们用排列树的方法来做：

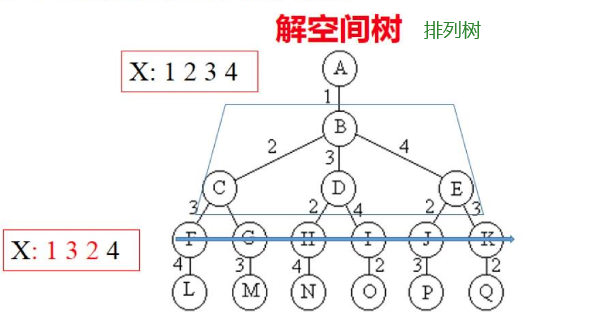
在这里插入图片描述

三、代码

//5-9 旅行售货员问题
//排列树
//指定从1出发，所以BackTrack(2) 
#include<iostream>
#include<string.h> 
#define INF 0x3f3f3f3f
using namespace std; 
int a[10][10];
int n;//顶点数 
int x[100];//当前解 
int bestx[100];//当前最优解 
int cc;//当前费用:不包括环路 
int bestc = INF;//当前最优值
void Init(){for(int i=1;i<=n;i++){x[i]=i;for(int j=1;j<=n;j++){if(i==j) a[i][j]=0;else a[i][j]=INF;}}}
void Print(int b[100]){for(int i=1;i<=n;i++)cout<<b[i]<<" ";cout<<endl;
}
void Swap(int &a,int &b){int t=a;a=b;b=t;
}
//排列树
void BackTrack(int t){ //第t个顶点 
//	cout<<" t = "<<t<<endl;if(t==n){//到达叶结点
//		Print();int c;if(a[x[n-1]][x[n]] !=INF && a[x[n]][x[1]]!=INF){//构成环路 c = cc+a[x[n-1]][x[n]]+a[x[n]][x[1]];if(c<bestc) {bestc=c;for(int j=1;j<=n;j++)bestx[j]=x[j];}}Print(x);cout<<"c="<<c<<endl;return;}else{for(int i=t;i<=n;i++){//是否可以进入x[i]子树 //	cout<<a[x[t-1]][x[i]]<<"  "<<cc+a[x[t-1]][x[i]]<<endl; cout<<"i="<<i<<endl;if(a[x[t-1]][x[i]] !=INF && cc+a[x[t-1]][x[i]]<bestc){Swap(x[t],x[i]);cc+=a[x[t-1]][x[t]];BackTrack(t+1);cc-=a[x[t-1]][x[t]];Swap(x[t],x[i]);}}	}	
} 
int main(){int t;//边数 int x,y,z;cin>>n>>t;memset(a,INF,sizeof(a));Init();for(int i=1;i<=t;i++){cin>>x>>y>>z;a[x][y]=z;a[y][x]=z;//无向图 }cout<<"--------------\n"; BackTrack(2); cout<<"bestc="<<bestc<<endl;return 0;
}
/*
4
6
1 2   30
1 3   6
1 4   5
2 3   4
2 4   10
3 4   20
*/