java语言解决旅行售货员问题（分支限界法）

2023-11-11 22:40
文章标签 java 语言 问题 解决 分支 旅行 限界 售货员

本文主要是介绍java语言解决旅行售货员问题（分支限界法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

1、什么是旅行售货员问题

1.1基本介绍

2.问题描述

3.代码实现 

1、什么是旅行售货员问题

旅行售货员问题(travelling salesman problem)是一类组合最优化问题，设有一个售货员从城市1出发，到城市2，3，…，n去推销货物，最后回到城市1.假定任意两个城市i，j间的距离dij(dij=dji)是已知的，问他应沿着什么样的路线走，才能使走过的路线最短?容易看出，中国邮递员问题要求走遍所有“线”，而后者要求走遍所有“点”，旅行售货员问题就是在一个完全网络中，找出一个具有最小权的哈密顿圈，寻求旅行售货员问题的有效算法似乎是没有希望的，它属于NP完全类，一个可行的办法是首先求一个哈密顿圈，然后适当修改，以得到具较小权的另一个哈密顿圈，旅行售货员问题有着明显的实际意义，除售货员之外，邮局里负责到各个信箱取信的邮递员，以及去各个分局送邮件的汽车等都会类似地遇到这个问题，还有一些问题表面上似乎与之无关，而实质上却可以归结为旅行售货员问题求解，如计算机线路问题、无中间存储的工件加工问题等 [1]  。

1.1基本介绍

设有p个城镇，已知每两个城镇之间的距离，一个售货员从某一城镇出发巡回售货，问这个售货员应如何选择路线，能使每个城镇经过一次且仅一次，最后返回到出发地，而使总的行程最短？这个问题称为旅行售货员问题。容易看出，旅行售货员问题就是在一个赋权完全图中找一个具有最小权的Hamilton圈，我们称这种圈为最优Hamilton圈。

除旅行售货员问题之外，邮局中负责到各个信箱取信的邮递员，以及去各个分局送邮件的汽车等都会类似遇到这种问题，还有一些问题表面上似乎与之无关，而实质上却可以归结为旅行售货员问题来解决，既然这个问题有着如此广泛的应用，那么找一个求解最优Hamilton圈的有效算法就成为一件非常重要的事 [2]  。

2.问题描述


某售货员要到若干城市去推销商品，已知各城市之间的路程（或旅费）。他要选定一条从驻地出发，经过每个城市一遍，最后回到驻地的路线，使总的路程（ 或旅费）最小。各个城市之间可能是有向连通的、无向连通的、以及存在某个城市不连通的情况，你的程序应该能够处理所有可能的情况。如下图表示各个城市间无向连通。

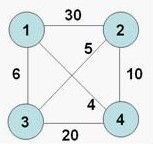
 输入：
第一行为一个整数n(n<=10)，表示城市的总个数。接下来是一个n*n的矩阵，用来表示城市间的连通情况以及花费，例如path[i][j]=len，len=-1表示从城市i到城市j没有通路，len>0表示从i到j的路程长度为len。对于上面图示的问题我们可以按照下面方式输入：

4
-1 30 6 4
30 -1 5 10
6 5 -1 20
4 10 20 -1

输出：25

3.代码实现 


import java.util.Scanner;
public class ts
{
public static void main(String args[])
{
Scanner s=new Scanner(System.in);
int n=0;//结点的个数
String line=s.nextLine();//读入n
n=Integer.parseInt(line);
a=new float[n][n];
int []vv=new int[n];for(int i=0;i<n;i++)
{
line=s.nextLine();
String []sArray=line.split(" ");
for(int j=0;j<sArray.length;j++)
{
a[i][j]=Integer.parseInt(sArray[j]);
}
}
System.out.println(bbTsp(vv));
}
static float [][]a;
private static class HeapNode implements Comparable
{
float lcost,//子树费用下界
cc,//当前费用
rcost;//X[s:n-1]中顶点最小出边费用和
int s;//根节点到当前结点的路径为X[0:s]
int []x;//需要进一步搜索的结点是x[s+1:n-1]
//HeapNode的构造函数
HeapNode(float lc,float ccc,float rc,int ss,int []xx)
{
lcost=lc;
cc=ccc;
s=ss;
x=xx;
}//HeapNode 构造函数
public int compareTo(Object x)
{
float xlc=((HeapNode)x).lcost;
if(lcost<xlc)
return -1;
if(lcost==xlc)
return 0;
return 1;
}
}
public static int  bbTsp(int []v)
{
int n=v.length;
MinHeap heap=new MinHeap(100);
float []minOut=new float[n];//minOut[i]是顶点i的最小出边费用
float minSum=0;//最小出边费用和
//计算最小出边费用和
for(int i=0;i<n;i++)
{
float min=Float.MAX_VALUE;
for(int j=0;j<n;j++)
{
if(a[i][j]!=-1&&a[i][j]<min)
min=a[i][j];//有回路
}//for j
if(min==Float.MAX_VALUE)
{
return -1;//无回路
}
minOut[i]=min;
minSum+=min;
}
int []x=new int[n];
for(int i=0;i<n;i++)
{
x[i]=i;
}
HeapNode enode=new HeapNode(0,0,minSum,0,x);
float bestc=Float.MAX_VALUE;
//搜索排列空间树
while(enode!=null&&enode.s<n-1)
{
//System.out.println(bestc);
x=enode.x;
if(enode.s==n-2)//叶子结点
{
if(a[x[n-2]][x[n-1]]!=-1&&
a[x[n-1]][1]!=-1||
bestc==Float.MAX_VALUE)//当前最优解还不存在的情况
{
bestc=enode.cc+a[x[n-2]][x[n-1]]+a[x[n-1]][0];
enode.cc=bestc;
enode.lcost=bestc;
enode.s++;
heap.put(enode);
}
}
else
{
for(int i=enode.s+1;i<n;i++)
{
if(a[x[enode.s]][x[i]]!=-1)
{
float cc=enode.cc+a[x[enode.s]][x[i]];
float rcost=enode.rcost-minOut[x[enode.s]];
float b=cc+rcost;
if(b<bestc)
{
int []xx=new int[n];
for(int j=0;j<n;j++)
xx[j]=x[j];
xx[enode.s+1]=x[i];
xx[i]=x[enode.s+1];
HeapNode node=new HeapNode(b,cc,rcost,enode.s+1,xx);
heap.put(node);
}
}
}
}
enode=(HeapNode)heap.removeMin();
}
for(int i=0;i<n;i++)
v[i]=x[i];
return (int)bestc;
}
public static class MinHeap
{
private HeapNode[] heapArray; // 堆容器
private int maxSize; // 堆的最大大小
private int currentSize=0; // 堆大小
//构造函数
public MinHeap(int _maxSize)
{
maxSize = _maxSize;
heapArray = new HeapNode[maxSize];
currentSize = 0;
}
//自上而下调整
public void filterDown(int start, int endOfHeap)
{
int i = start;
int j = 2 * i + 1; // j是i的左子女位置
HeapNode temp = heapArray[i];
while (j <= endOfHeap)
{ // 检查是否到最后位置
if (j < endOfHeap // 让j指向两子女中的小者
&& heapArray[j].cc > heapArray[j + 1].cc)
{
j++;
}
if (temp.cc <= heapArray[j].cc)
{ // 小则不做调整
break;
} else
{ // 否则小者上移，i，j下降
heapArray[i] = heapArray[j];
i = j;
j = 2 * j + 1;
}
}
heapArray[i] = temp;
}//filterDown//自下而上的调整:从结点start开始到0为止，自下向上比较，如果子女的值小于双亲结点的值则互相交换
public void filterUp(int start)
{
int j = start;
int i = (j - 1) / 2;
HeapNode temp = heapArray[j];while (j > 0)
{ // 沿双亲结点路径向上直达根节点
if (heapArray[i].cc <= temp.cc)
{// 双亲结点值小，不调整
break;
} else {// 双亲结点值大，调整
heapArray[j] = heapArray[i];
j = i;
i = (i - 1) / 2;
}
heapArray[j] = temp; // 回送
}
}//filterUp//插入结点
public void put(HeapNode node)
{
HeapNode newNode = node;
heapArray[currentSize] = newNode;
filterUp(currentSize);
currentSize++;
}
//删除堆中的最小值
public HeapNode removeMin()
{
HeapNode root = heapArray[0];
heapArray[0] = heapArray[currentSize - 1];
currentSize--;
filterDown(0, currentSize - 1);
return root;
}
}
}

 实例输入

这篇关于java语言解决旅行售货员问题（分支限界法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/393300。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
Spring Security 基于表达式的权限控制

Spring Security 基于表达式的权限控制

前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
阅读更多...
浅析Spring Security认证过程

浅析Spring Security认证过程

类图 为了方便理解Spring Security认证流程，特意画了如下的类图，包含相关的核心认证类 概述 核心验证器 AuthenticationManager 该对象提供了认证方法的入口，接收一个Authentiaton对象作为参数; public interface AuthenticationManager {Authentication authenticate(Authenti
阅读更多...
Spring Security--Architecture Overview

Spring Security--Architecture Overview

1 核心组件 这一节主要介绍一些在Spring Security中常见且核心的Java类，它们之间的依赖，构建起了整个框架。想要理解整个架构，最起码得对这些类眼熟。 1.1 SecurityContextHolder SecurityContextHolder用于存储安全上下文（security context）的信息。当前操作的用户是谁，该用户是否已经被认证，他拥有哪些角色权限…这些都被保
阅读更多...
Spring Security基于数据库验证流程详解

Spring Security基于数据库验证流程详解

Spring Security 校验流程图 相关解释说明（认真看哦） AbstractAuthenticationProcessingFilter 抽象类 /*** 调用 #requiresAuthentication(HttpServletRequest, HttpServletResponse) 决定是否需要进行验证操作。* 如果需要验证，则会调用 #attemptAuthentica
阅读更多...
Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
Java架构师知识体认识

Java架构师知识体认识

源码分析 常用设计模式 Proxy代理模式Factory工厂模式Singleton单例模式Delegate委派模式Strategy策略模式Prototype原型模式Template模板模式 Spring5 beans 接口实例化代理Bean操作 Context Ioc容器设计原理及高级特性Aop设计原理Factorybean与Beanfactory Transaction 声明式事物
阅读更多...
Java进阶13讲__第12讲_1/2

Java进阶13讲__第12讲_1/2

多线程、线程池 1.  线程概念 1.1  什么是线程 1.2  线程的好处 2.   创建线程的三种方式 注意事项 2.1  继承Thread类 2.1.1 认识  2.1.2  编码实现  package cn.hdc.oop10.Thread;import org.slf4j.Logger;import org.slf4j.LoggerFactory
阅读更多...
好题——hdu2522（小数问题：求1/n的第一个循环节）

好题——hdu2522（小数问题：求1/n的第一个循环节）

好喜欢这题，第一次做小数问题，一开始真心没思路，然后参考了网上的一些资料。 知识点***********************************无限不循环小数即无理数，不能写作两整数之比*****************************（一开始没想到，小学没学好） 此题1/n肯定是一个有限循环小数，了解这些后就能做此题了。 按照除法的机制，用一个函数表示出来就可以了，代码如下
阅读更多...
hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

hdu1043（八数码问题，广搜 + hash（实现状态压缩） ）

利用康拓展开将一个排列映射成一个自然数，然后就变成了普通的广搜题。 #include<iostream>#include<algorithm>#include<string>#include<stack>#include<queue>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#inclu
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2