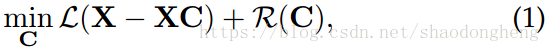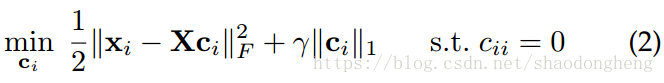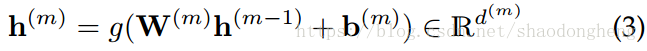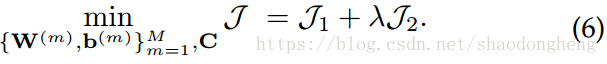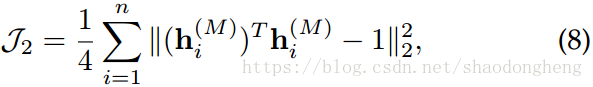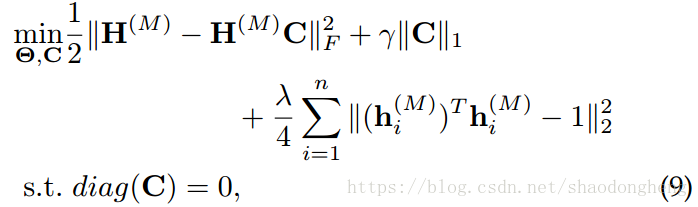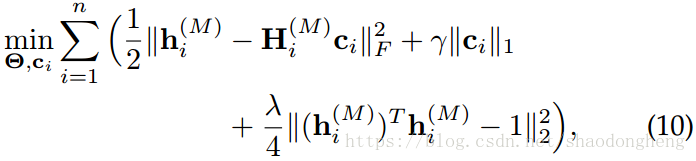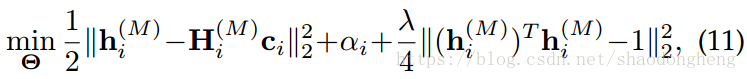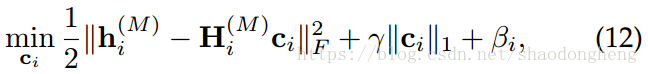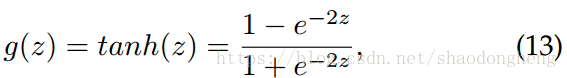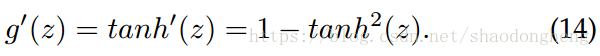Deep Sparse Subspace Clustering 翻译

本文主要是介绍Deep Sparse Subspace Clustering 翻译，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Deep Sparse Subspace Clustering 翻译

文章下载：http://cn.arxiv.org/pdf/1709.08374

摘要：

在本文中，我们提出了稀疏子空间聚类的深度扩展，称为深度稀疏子空间聚类（DSSC）。通过对学习的深度特征的单位球分布假设进行规范，DSSC可以通过同时满足SSC的稀疏性原理和神经网络给出的非线性来推断出新的数据亲和度矩阵。 DSSC带来的吸引人的优势之一是：当原始现实世界数据不满足特定类的线性子空间分布假设时，DSSC可以使用神经网络通过其分层非线性变换使假设有效。据我们所知，这是第一个基于深度学习的子空间聚类方法。对四个真实世界数据集进行了大量实验，以表明所提出的DSSC明显优于现有的12种子空间聚类方法。

1 引言

子空间聚类旨在同时隐式地找出基础子空间以适合每组数据点并基于所学习的子空间执行聚类，这引起了计算机视觉和图像处理社区的极大兴趣。大多数现有的子空间聚类方法可大致分为以下几类：代数方法，迭代方法，统计方法和基于谱聚类的方法。

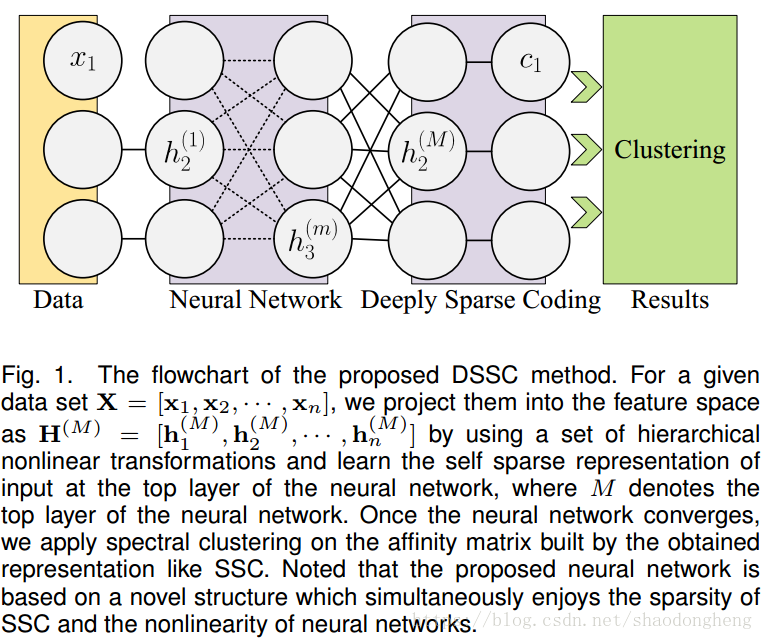
最近，已经提出了大量基于谱聚类的方法，其首先使用整个数据集的线性重建系数形成亲和度矩阵，然后通过在亲和度矩阵上应用谱聚类来获得聚类结果。这些方法彼此不同主要在于它们在系数上采用的先验。例如，基于1范数的稀疏子空间聚类（SSC）及其基于0范数的变量，低秩表示（LRR）和阈值岭回归（TRR）使用线性表示系数在不同约束下构建亲和度矩阵，约束分别为 $\boldsymbol{l}_{1}$ -范数，核 -范数和 $\boldsymbol{l}_{2}$ - 范数。形式上，SSC，LRR，TRR以及它们的许多变体通过以下方式学习表示系数以构建亲和度矩阵：

表示输入的线性表示。d表示数据的维度，n表示样本数据的数目。表示C上的结构先验，而表示误差函数的选择通常取决于X的分布假设，例如，一个典型的损失函数是

尽管这些方法在子空间聚类方面取得了令人印象深刻的性能，但它们通常受到以下限制。首先，这些方法假设每个样本可以通过整个样本集合进行线性重建。然而，在实际情况中，数据可能不能在输入空间中互相线性地表示。因此，这些方法的表现通常会在实践中下降。为了解决这个问题，最近的一些工作开发了基于内核的方法，这些方法已经证明了它们在子空间聚类中的有效性。但是，基于内核的方法类似于基于模板的方法，其性能在很大程度上取决于内核函数的选择。而且，这些方法不能给出明确的非线性变换，导致处理大规模数据集时的困难。

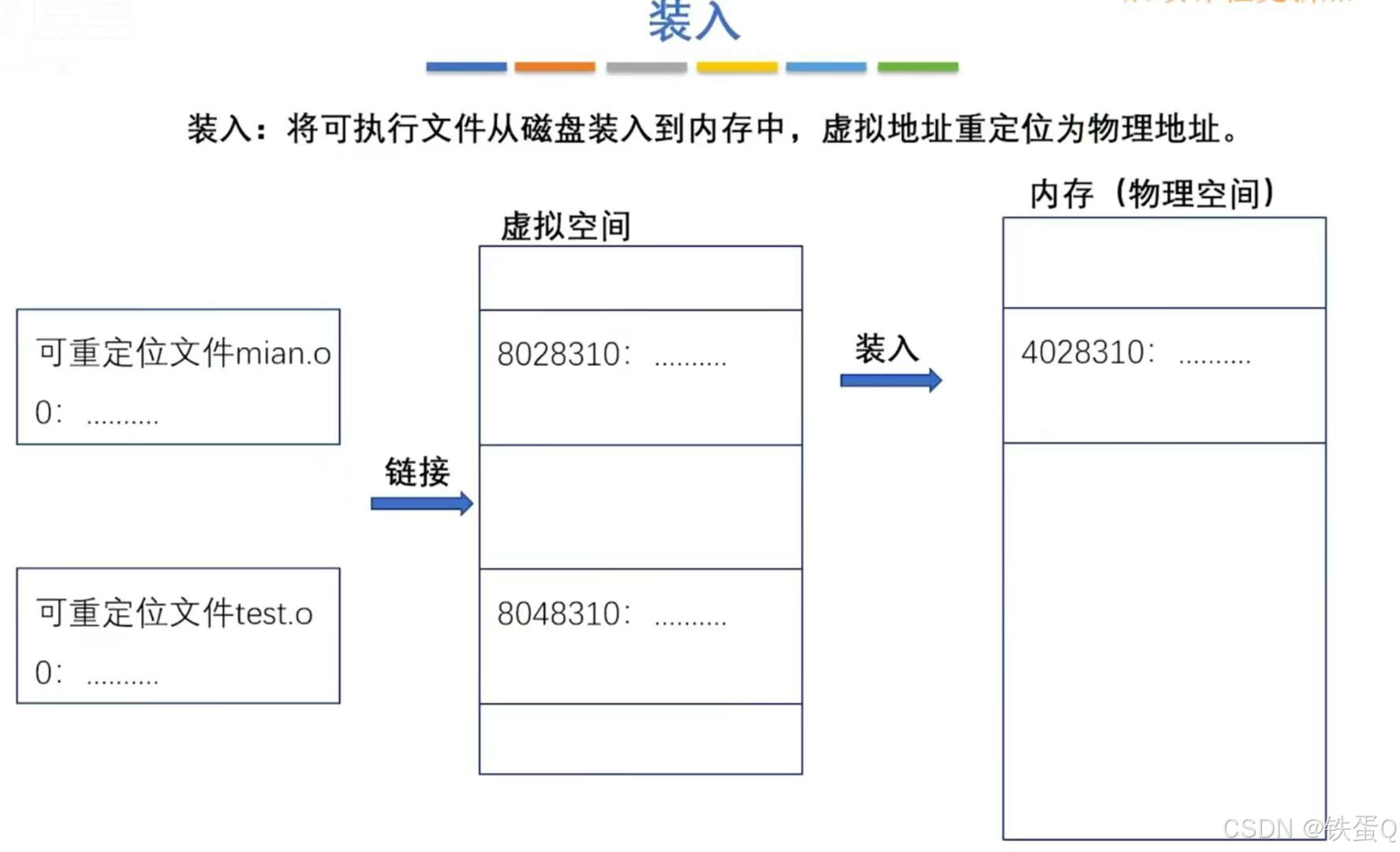
受到深度学习在各种应用中取得的巨大成功的启发，在这项工作中，我们提出了一种基于神经网络的新子空间聚类框架，称为深度稀疏子空间聚类（DSSC）。 DSSC的基本思想（见图1）简单但有效。它使用神经网络将数据投影到另一个空间，其中SSC对非线性子空间情况有效。与大多数现有的子空间聚类方法不同，我们的方法同时学习由神经网络参数化的一组分层变换，并且重构系数将每个映射的样本表示为其他的组合。与基于内核的方法相比，DSSC是深度而非浅层模型，可以将输入空间中的样本显式映射到潜在空间，并以数据驱动的方式学习转换中的参数。据我们所知，DSSC是SSC的第一个深度扩展，它满足SSC的稀疏性原则，同时使SSC对非线性子空间情况有效。

图1.提出的DSSC方法的流程图。对于给定的数据集，我们通过使用一组分层非线性变换将它们投影到的特征空间中，并在神经网络的顶层学习输入的自稀疏表示，其中M表示顶层神经网络。一旦神经网络收敛，我们将谱聚类应用于由所获得的表示（如SSC）构建的亲和度矩阵。注意到所提出的神经网络基于一种新颖的结构，同时享有SSC的稀疏性和神经网络的非线性。

这项工作的贡献是双重的。从子空间聚类的角度，我们展示了如何使其受益于深度神经网络的成功，从而可以实现非线性子空间聚类。从神经网络的角度，我们证明了将现有子空间聚类方法和深度学习的优点结合起来开发新的无监督学习算法是可行的。

符号：在整篇论文中，小写粗体字母表示列向量，大写字母粗体表示矩阵。 $A^{T}$ 表示矩阵A的转置， $\mathbf{I}$ 表示单位矩阵。

2 相关工作

子空间聚类：在过去的十年中，子空间聚类方法的兴起在计算机视觉中具有各种应用，例如，运动分割，人脸聚类，图像处理，多视图分析和视频分析。特别地，在这些工作中，基于光谱聚类的方法已经实现了最先进的结果。这些方法的关键是学习令人满意的亲和度矩阵A，其中 $A_{ij}$ 表示第i个样本和第j个样本之间的相似性。理想情况下，仅当相应的数据点 $x_{i}$ 和 $x_{j}$ 是从同一子空间中绘制时才是 $\mathbf{A}_{ij}\neq 0$ 。为此，一些最近的工作（例如SSC）假设任何给定的样本可以由输入空间中的其他样本线性重建。基于自表示，可以构建亲和度矩阵（或称为相似性图）并将其馈送到谱聚类算法以获得最终的聚类结果。然而，在实践中，高维数据（例如面部图像）通常驻留在非线性流形上。不幸的是，在原始空间中可能不满足线性重建假设，并且在这种情况下，该方法可能无法捕获流形的固有非线性。为了解决这个限制，内核方法用于首先将样本投影到高维特征空间中，在该高维特征空间中计算整个数据集的表示。之后，通过在内核空间中执行传统的子空间聚类方法来实现聚类结果。但是，基于内核的方法的行为类似于基于模板的方法，这些方法通常需要有关数据分布的先验知识才能选择理想的内核函数。显然，这种先验在实践中很难获得。而且，他们无法从数据集中学习明确的非线性映射函数，因此会遇到可扩展性问题和样本外问题。

与这些经典子空间聚类方法不同，我们的方法从数据集中学习一组显式非线性映射函数，以将输入映射到另一个空间，并使用新空间中的样本表示来计算亲和度矩阵。

深度学习：旨在从输入中学习高阶特征，深度学习在监督学习的场景中的许多计算机视觉任务中显示出有前景的结果，例如图像分类。相比之下，对无监督学习方案的应用的关注较少。最近，一些工作致力于将深度学习和无监督聚类相结合，并且在传统的聚类方法上显示出令人印象深刻的结果。这些方法具有相同的基本思想，即使用深度学习来学习良好的表示，然后利用现有的聚类方法（如k-means）实现聚类。它们之间的主要区别在于神经网络结构和目标函数。

与这些工作不同，我们的框架基于新的神经网络而不是现有的网络。此外，我们的方法侧重于子空间聚类而不是聚类，它同时以联合的方式从输入和自我表示中学习高阶特征，而这些现有方法不具备自我表示子空间聚类的有效性。我们认为这种通用框架是对现有浅子空间聚类方法的补充，因为它可以采用这些方法中的损失函数和正则化。据我们所知，这是前几种深度子空间聚类方法之一。需要指出的是，我们的模型与下面也有很大的不同：1）执行流形学习，这要求数据可以在输入空间中线性重建，并将获得的稀疏表示从输入空间嵌入到潜在空间中。相反，我们的模型旨在解决非线性子空间聚类的问题，即数据不能在输入空间中线性表示。 2）在【49】中，稀疏表示被用作先验类型，它保持不变。相比之下，这项工作动态地寻求良好的稀疏表示来共同优化我们的神经网络。 3）所提出的方法可以看作是众所周知的SSC的深度非线性扩展，这使得SSC处理非线性子空间聚类成为可能。

3 深度稀疏子空间聚类

在本节中，我们首先简要回顾一下SSC，然后介绍我们的深子空间聚类方法的细节。

3.1 稀疏子空间聚类

对于一个给定的数据集，SSC寻求使用一些其他样本线性重建第i个样本 $\mathbf{x}_{i}$ 。换句话说，表示系数被期望是稀疏的。为实现这一目标，问题的表述如下，

其中 $\left \| \cdot \right \|_{1}$ 表示 $\boldsymbol{l}_{1}$ -范数（即，矢量中所有元素的绝对值之和），其充当 $\boldsymbol{l}_{0}$ -范数的弛豫，并且 $c_{ii}$ 表示 $\mathbf{c}_{i}$ 中的第i个元素。具体来说，惩罚 $\left \| \mathbf{c_{i}} \right \|_{1}$ 会鼓励 $\mathbf{c}_{i}$ 稀疏，并强制执行约束 $c_{ii}$ = 0以避免平凡解。为了解决（2）中的优化问题，经常使用乘法器的交替方向法（ADMM）。

一旦通过求解（2）获得整个数据集的稀疏表示，则SSC中的亲和度矩阵被计算为，基于亲和度矩阵应用谱聚类以给出聚类结果。

3.2 深度子空间聚类

在包括SSC的大多数现有子空间聚类方法中，每个样本被编码为整个数据集的线性组合。然而，当处理通常位于非线性流形上的高维数据时，这种方法可能无法捕获非线性结构，从而导致较差的结果。为了解决这个问题，我们提出了一种基于深度学习的方法，该方法使用神经网络中的明确的分层变换来映射给定样本，并同时学习重构系数以将每个映射样本表示为其他的组合。

如图1所示，我们提出的框架中的神经网络由M + 1个堆叠层组成，具有M个非线性变换，它将给定样本x作为第一层的输入。为便于演示，我们在下面做出几个定义。对于神经网络的第一层，我们将其输入定义为。而且，对于后续层，让

是第m层的输出（其中m = 1，2，··· M 是该层索引），其中g（·）是非线性激活函数， $d^{\left ( m \right )}$ 是第m层输出的维数，分别表示第m层的权重和偏差。特别是，给定x作为第一层的输入，我们的神经网络顶层的输出是

实际上，如果将上面的表达式表示为f（x），我们可以观察到是由我们的神经网络的权重和偏差确定的非线性函数（即，）以及激活函数g（·）的选择。此外，对于n个样本，我们将 $\mathbf{H}^{\left ( M \right )}$ 定义为由我们的神经网络给出的相应输出的集合，即

通过上述定义，我们以下列形式提出了我们方法的目标函数：

其中λ是正折衷参数，定义如下。直观地说，第一项旨在最小化与其自我表达之间的差异。此外，它同时将C调整为某些所需的属性。具体而言，可以表示为

其中如果C不在某些可行域中，则取 $+\infty$ 的值，否则为0。注意，的形式可以从许多现有的子空间聚类工作中采用。在本文中，我们的目标是开发SSC的深度扩展，因此如果是被违反的，则取，，，否则。

第二部分旨在消除潜在空间中的任意缩放因子。在这项工作中，我们设定

注意到，如果没有上述术语，我们的神经网络可能会在像这样的平凡解中崩溃。

对于上面详述的，我们提出的DSSC的优化问题可以表示如下：

其中Θ表示参数化神经网络，即。

3.3 优化

为了便于演示，我们首先重写（9）如下：

其中是的变体，其通过简单地将中的替换为 0 而获得。

给定n个数据点，DSSC通过求解（10）同时学习M个非线性映射函数和n个稀疏编码。由于（10）是一个多变量优化问题，我们采用交替最小化算法，通过交替更新其中一个变量，同时固定其他变量。

步骤1：固定 $c_{i}$ 和 $\mathbf{H}_{i}^{\left ( m \right )}$ ，更新 $\Theta$ ，（10）可以重写成

是一个常数。

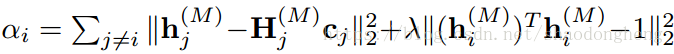
为了求解（11），我们采用随机子梯度下降（SGD）算法来获得参数。此外，我们还对参数实施 $\boldsymbol{l}_{2}$ -范数以避免过度拟合，其中正则化参数在所有实验中固定为 $\varphi = 10^{-3}$ 。注意到，（11）也可以用小批量SGD解决，特别是当数据量很大时。但是，小批量SGD可能会有两个问题。首先，它引入了新的超参数（即批量大小），这增加了人们对模型选择的努力。其次，高效率可能是以性能下降为代价的。

步骤2：固定，更新 $\mathbf{c}_{i}$

是一个常数，注意，（12）在SSC中是一个标准的 $\boldsymbol{l}_{1}$ -最小化问题，它可以通过使用现有的 $\boldsymbol{l}_{1}$ -解决法【58】来解决.

重复步骤1和步骤2直到收敛。在获得C之后，我们通过构造相似图，并基于A得到聚类结果.DSSC的优化过程总结在算法1中。

3.4 讨论

我们的方法DSSC可以提供令人满意的子空间聚类性能，符合以下因素。首先，与SSC不同，DSSC在深度潜在空间而不是原始空间中执行稀疏编码，并且以数据驱动的方式自动学习潜在空间。在通过学习的变换矩阵将输入数据映射到潜在空间之后，变换的样本更有利于线性重建。其次，DSSC也可以被视为深度核方法，它以数据驱动的方式自动学习转换。考虑到基于核的子空间聚类方法（如[35]，[36]）所证明的有效性，由于深度神经网络的代表性能力，DSSC具有更好的子空间聚类性能。

需要指出的是，所提出的DSSC采用了类似的神经网络结构和深度度量学习网络（DMLNs），即一组完全连通的层来执行非线性变换，然后对神经网络的输出执行特定任务。它们之间的主要区别是：1）目标函数不同。我们的方法旨在将不同的样本分成不同的子空间，而这些度量学习网络旨在学习测量两个数据点的相似或相关程度的相似度函数; 2）我们的DSSC是无监督的，而DMLN是监督方法，需要标签信息来训练神经网络。