晴天的魔法乐园——上楼（组合数）

本文主要是介绍晴天的魔法乐园——上楼（组合数），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：https://judger.net/problem/1054

Problem Description

我打算走楼梯上楼，共有n级台阶。
我身轻如燕，所以每次都可以选择上一级台阶或者两级台阶。
问有多少种上楼的方式。
例如当n=3时，共有三种方式上楼：

一级 -> 一级 -> 一级；
一级 -> 二级；
二级 -> 一级。

Input

每个输入文件一组数据。
一个正整数n（n<=45），表示台阶级数。

Output

一个正整数，表示上楼的方案数。

Sample Input 1

Sample Output 1

Sample Input 2

Sample Output 2

Sample Input 3

Sample Output 3

1、分析

这种题目看都不用看，想都不用想，绝对是找规律的题。

（1）、找规律。

考虑一下情形：

n = 1时：1种，①：1

n = 2时：2种，①：1 + 1

②：2

n = 3时：3种，①：1 + 1 + 1

②：1 + 2

③：2 + 1

n = 4时：5种，①：1 + 1 + 1 + 1

②：1 + 1 + 2

③：1 + 2 + 1

④：2 + 1 + 1

⑤：2 + 2

n = 5时：8种，①：1 + 1 + 1 + 1 + 1

②：1 + 1 + 1 + 2

③：1 + 1 + 2 + 1

④：1 + 2 + 1 + 1

⑤：2 + 1 + 1 + 1

⑥：1 + 2 + 2

⑦：2 + 2 + 1

⑧：2 + 1 + 2

...

n=5时，总数=5个楼梯中选择0个2级楼梯的种类数 + 4个楼梯中选择1个2级楼梯的种类数 + 3个楼梯中选择2个两级楼梯的种类数。

听起来有点像组合数？没错，就是组合数。

即：

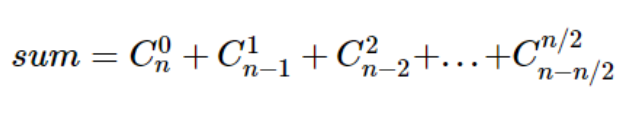
注意n为奇数和偶数都是计算到n/2向下取整处哦。

知道了以上规律之后，就是计算组合数的问题了。

（2）求组合数。

由于int所能表示的最大正整数2 ^ 31 - 1 = 2147483647‬ ≈ 2 * 10 ^ 9 < 13！；

long long所能表示的正整数：2 ^ 64 - 1 = 9223372036854775807‬ ≈ 9 * 10 ^ 18 < 21！；

因此不能表示最大45！的整数。因此采用下面最右边的公式进行计算。

有同学可能会考虑到整数相除会不精确，这里做除法的时候，需要增加一个判断，即(m - n + i) % i ==0的时候再相除。

2、代码

#include<stdio.h>//计算组合数m为下标，n为上标 
int fac(int m, int n){if(n == 0){return 1;}else if(n == 1){return m;}else{int plus = 1;		//每一步计算临时保存的结果 for(int i = 1; i <= n; i++){plus = plus * (m - n + i);if(plus % i == 0){	//当可以进行整除的时候再进行除法操作 plus /= i;}}return plus;}
}int main(){int n;scanf("%d", &n);int i = n, j = 0, sum = 0;while(i - j >= 0){	//当上标小于等于下标时才进行计算 sum += fac(i, j);i--;j++;}printf("%d\n", sum);return 0;
}