西北工业大学noj2023年c程序设计100题，更新中

本文主要是介绍西北工业大学noj2023年c程序设计100题，更新中，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

写在前面

这个是西北工业大学noj新版的解题思路，2023年更新的题库，我提供了比较复杂的题目的解题思路和方法，对于相对简单的题目则是只给出了代码，但是希望读者不要直接抄袭，因为这个课还是很重要的，是未来四年的基础，倘若有什么问题可以在评论区指出，

未来做完100道noj后可能会将题目上传到gitee和github上供参考，希望读者能从这个文章中有所收获

1.输出helloworld

#include<stdio.h>
int main(){printf("Hello World");
}

这个很简单没有什么好说的

2.输出a+b

#include<stdio.h>
int main(){int a,b,c;scanf("%d",&a);scanf("%d",&b);c=a+b;printf("%d",c);}

这个也很简单没有什么需要多说的

3.输出数据类型与范围

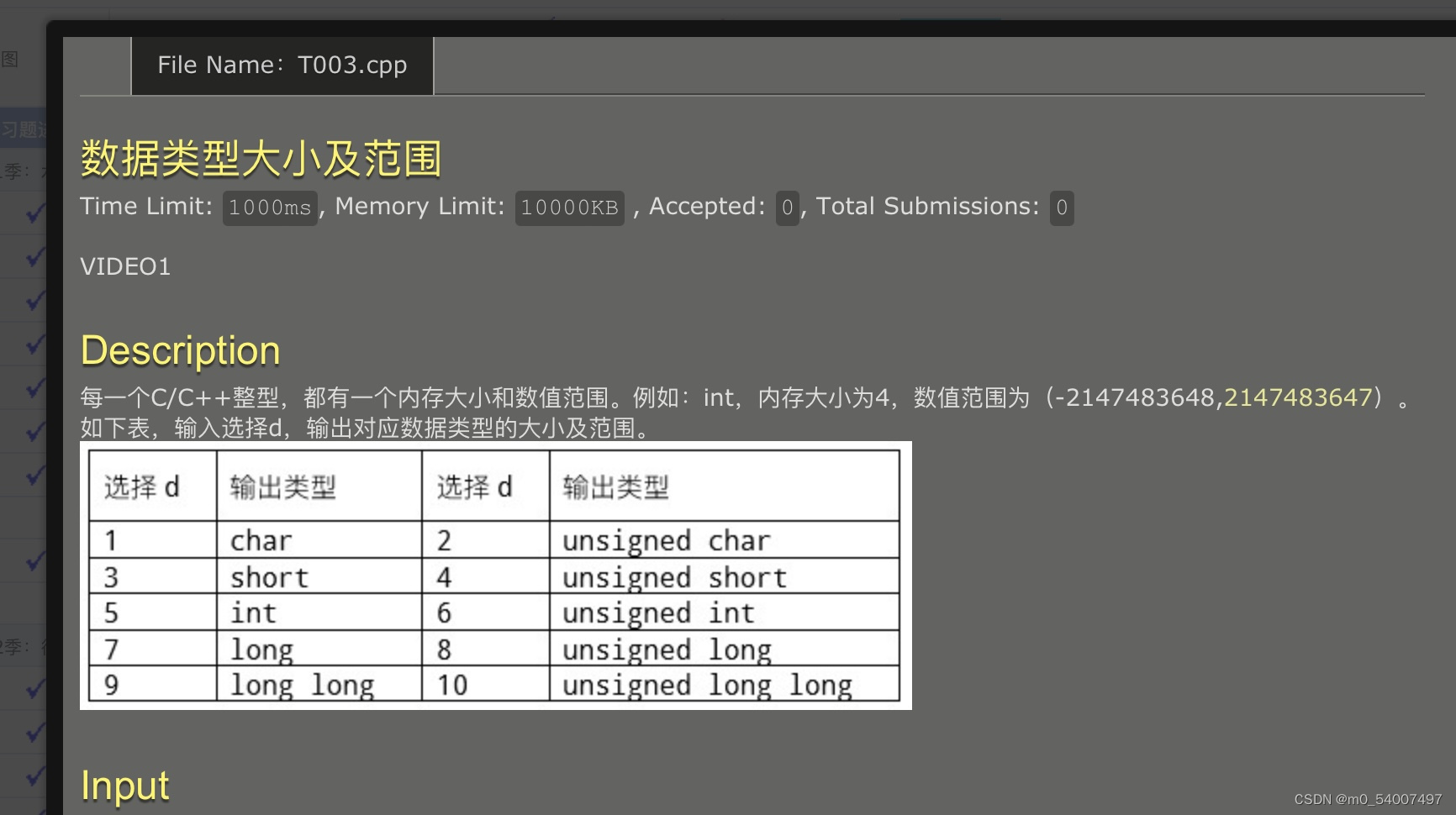
#include<stdio.h>int main(){int a;scanf("%d",&a);if(a==1){printf("1,-128,127");}if(a==2){printf("1,0,255");}if(a==3){printf("2,-32768,32767");}if(a==4){printf("2,0,65535");}if(a==5){printf("4,-2147483648,2147483647");}if(a==6){printf("4,0,4294967295");}if(a==7){printf("4,-2147483648,2147483647");}if(a==8){printf("4,0,4294967295");}if(a==9){printf("8,-9223372036854775808,9223372036854775807");}if(a==10){printf("8,0,18446744073709551615");}
}

需要注意是不是把数据范围打错了，可以根据这个代码参考修改数据

4.平均数

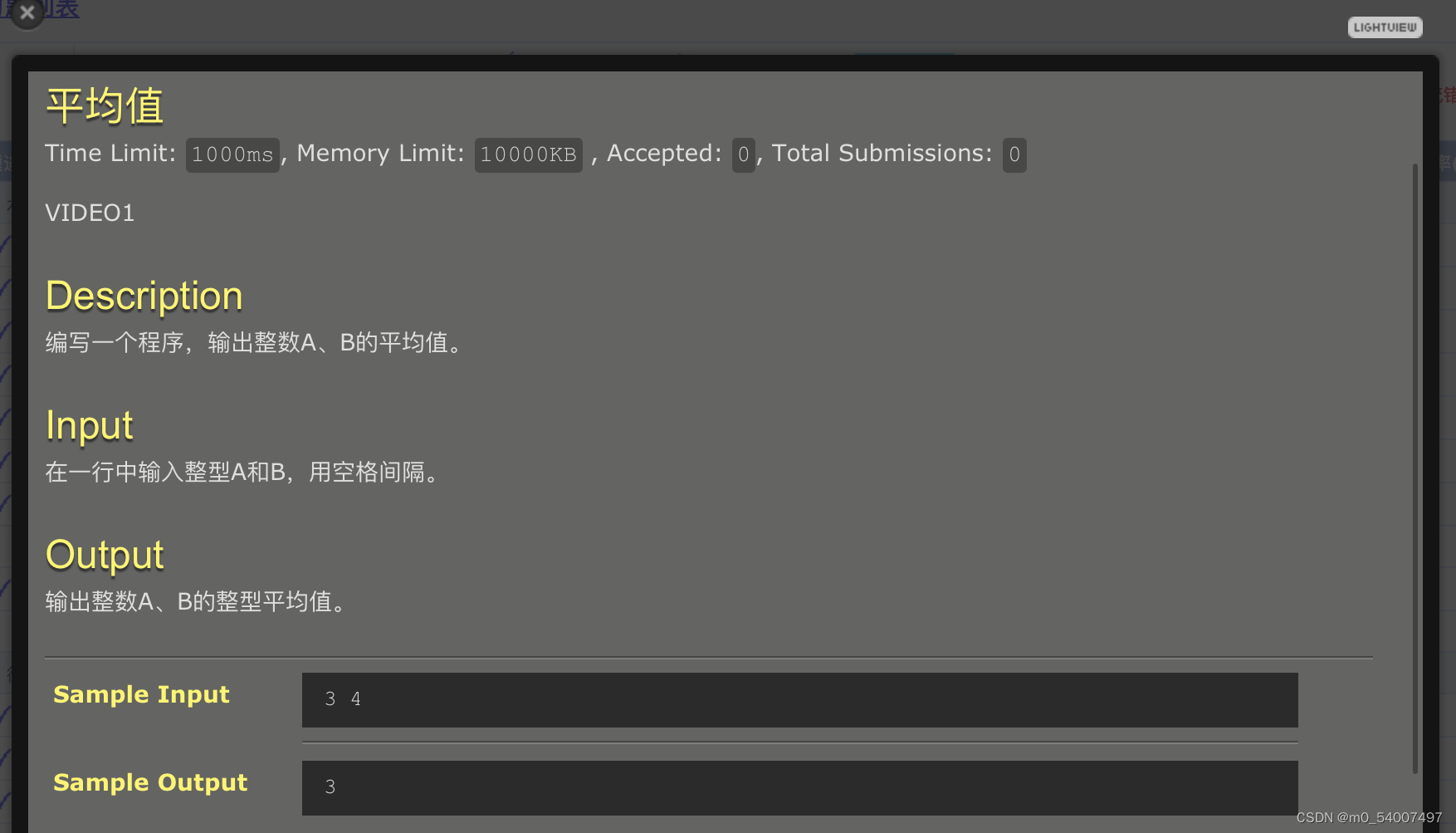
#include <stdio.h>int main() {long long  a, b;long long average;scanf("%lld",&a);scanf("%lld",&b);average = (a + b) / 2;printf("%lld\n",average);return 0;
}

新版noj中第一个重量级，需要用longlongint来存储数据，如果用int会过不了

5.进制转换

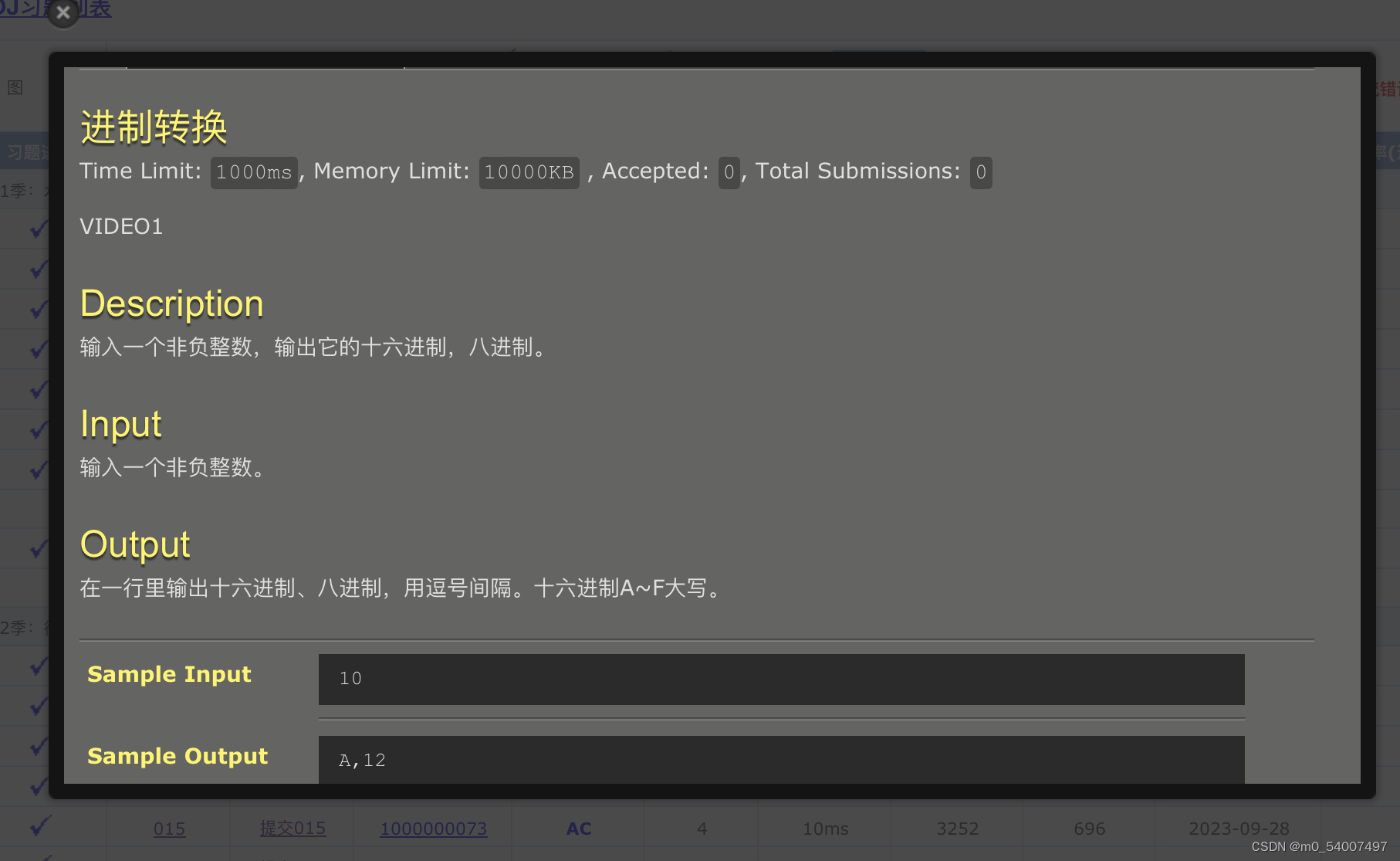
#include <stdio.h>int main() {unsigned int num; // 使用 unsigned int 来确保接受非负整数scanf("%u", &num);printf("%X,", num); // %x 用于输出十六进制printf("%o", num); // %o 用于输出八进制return 0;
}

注意输出的时候有个，其他非常简单

6.浮点数输出

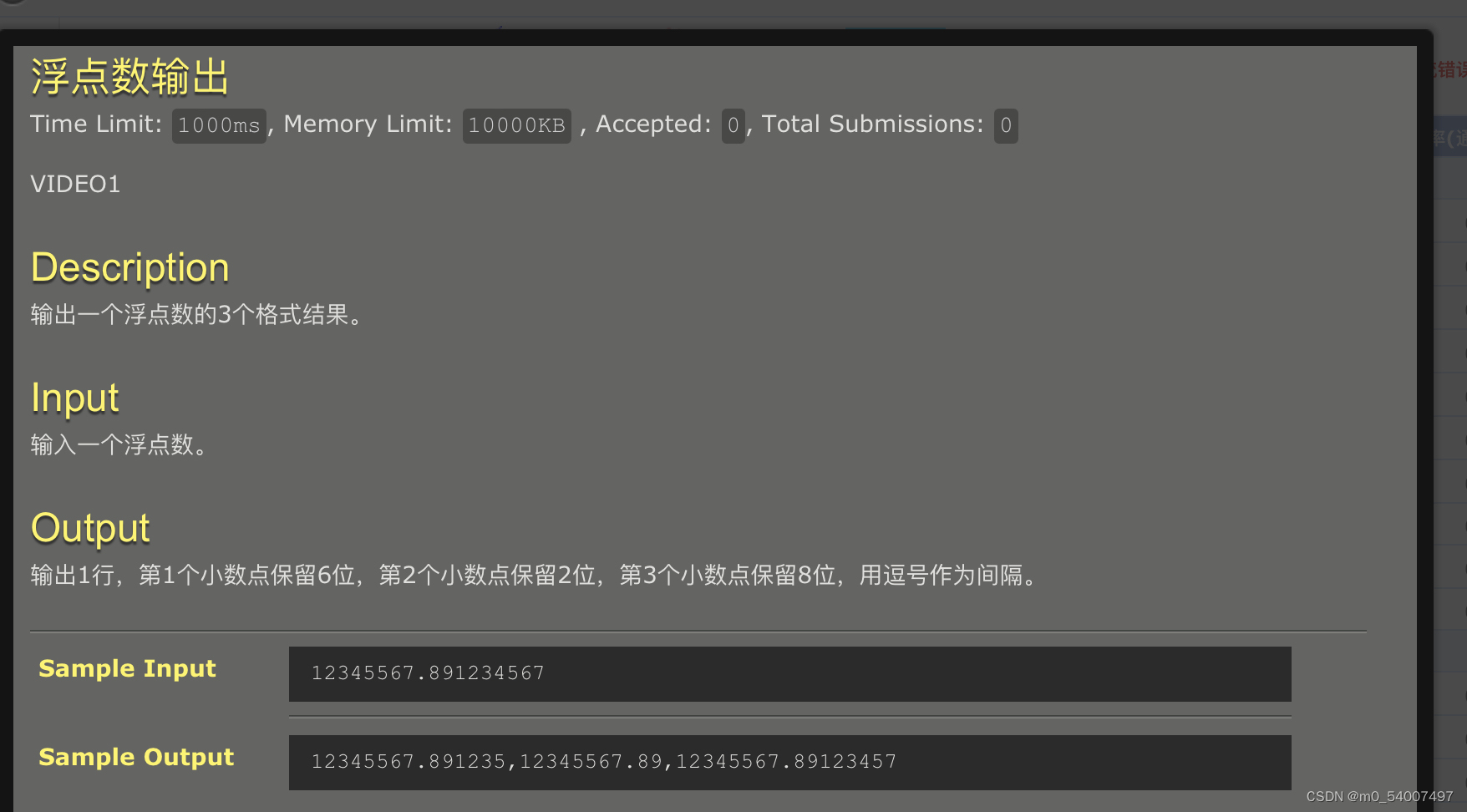
#include <stdio.h>int main() {double num;scanf("%lf", &num);printf("%.6lf,%.2lf,%.8lf\n", num, num, num);return 0;
}

不赘述

7.动态宽度输出

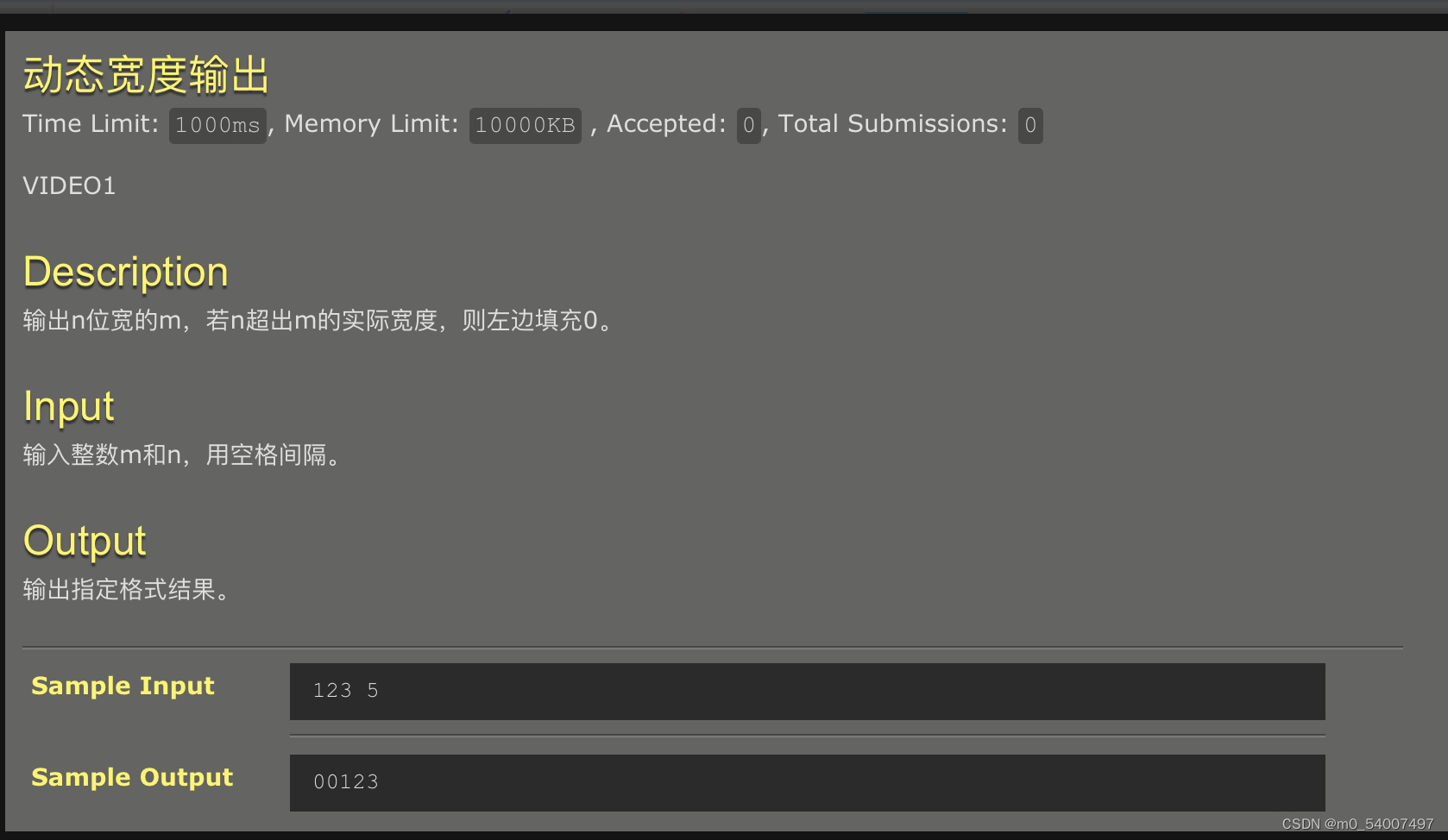
#include <stdio.h>int main() {int m, n;scanf("%d %d", &m, &n);printf("%0*d\n", n, m);return 0;
}

比较简单

8.计算地球上两点之间的距离

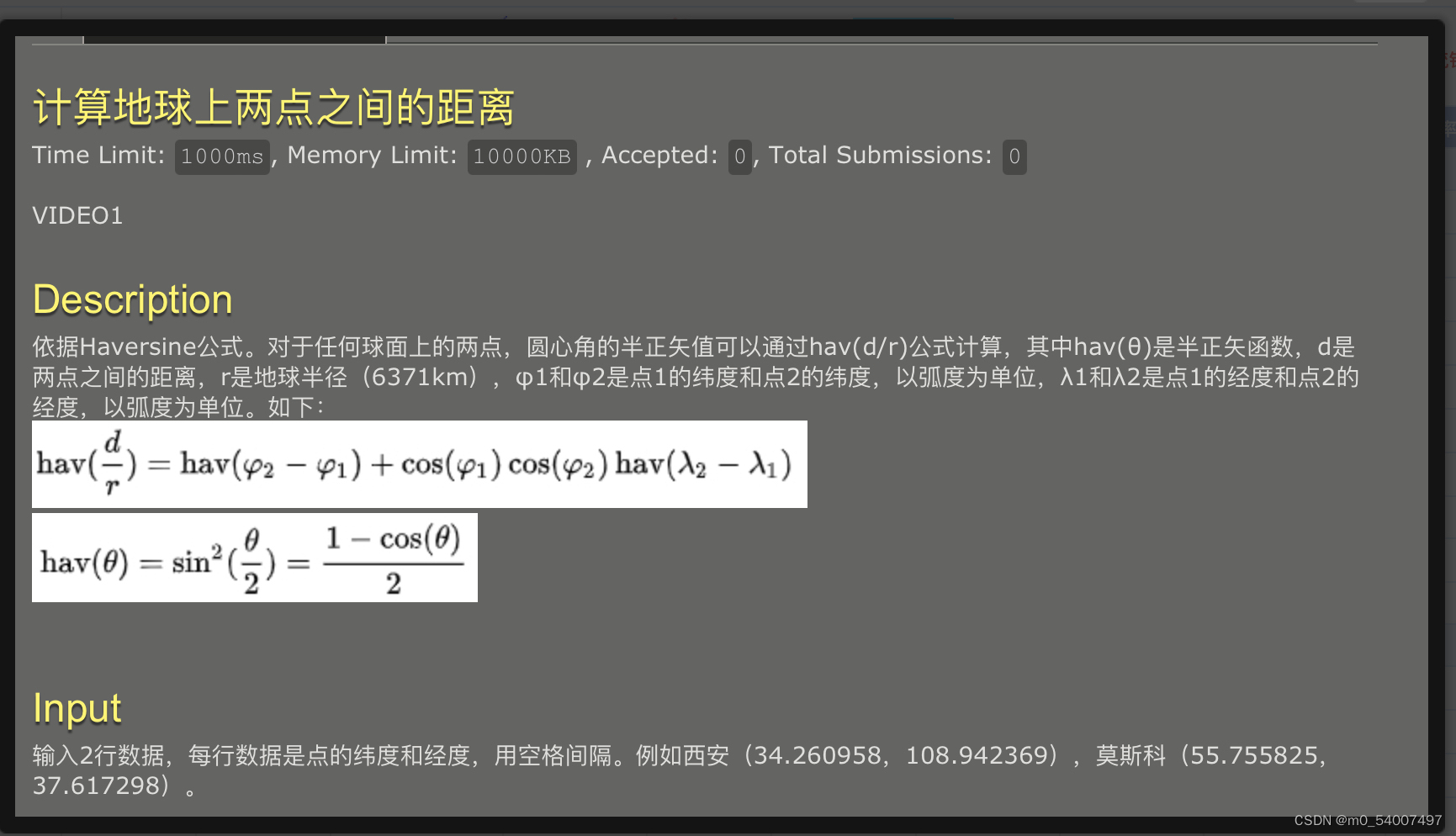
#include<stdio.h>
#include<math.h>
#define dpi 3.141592653589
#define R 6371
double getpi(int a){double pi=0.0;for(int i=0;i<a;i++){if(i%2==0){pi+=1.0/(2*i+1);}else{pi-=1.0/(2*i+1);}}return 4*pi;
}
double hav(double a){double b;b=(1-cos(a))/2;return b;}
double toRadis(double a){double b,pi;pi=getpi(100000);b=a*(dpi/180);return b;
}
double gethav(double a,double b,double c,double d){double i;double e,f,g,h;e=toRadis(a);f=toRadis(b);g=toRadis(c);h=toRadis(d);    i=hav(e-g)+cos(g)*cos(e)*hav(h-f);return i;
}
double figureout(double a){double result;result=R*acos(1-2*a);return result;
}
int main(){double a,b,c,d,e,f;scanf("%lf %lf%lf%lf",&a,&b,&c,&d);e=gethav(a,b,c,d);f=figureout(e);printf("%.4lfkm",f);
}

输出样例有问题，害人不浅

9.风寒指数

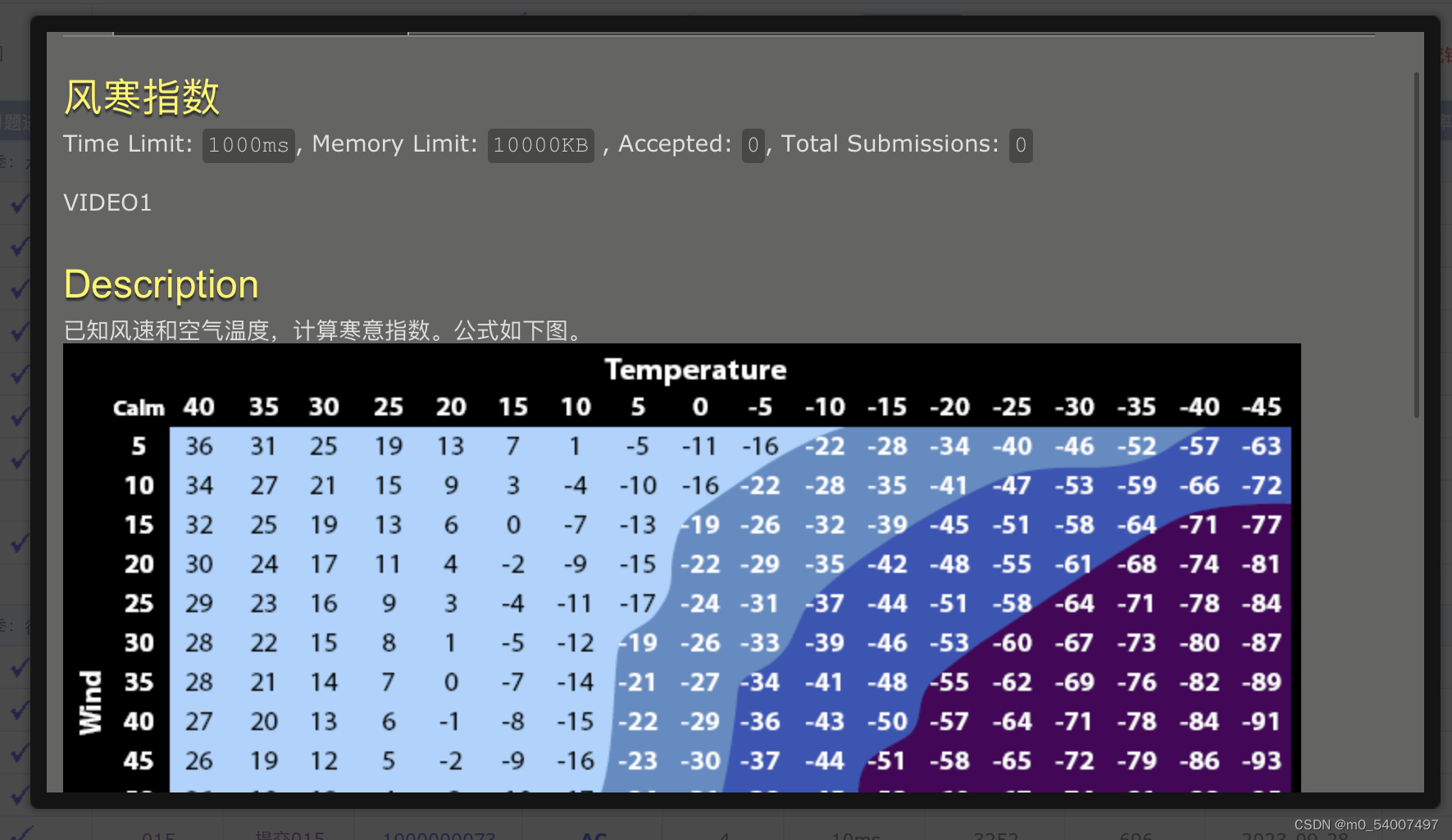
#include <stdio.h>
#include <math.h>
int myround (double x){return (int)(x+0.5);
}
int calculate_wind_chill(double v, double t) {double wind_chill = 13.12 + 0.6215*t - 11.37*pow(v, 0.16) + 0.3965*t*pow(v, 0.16);return myround(wind_chill);
}int main() {double v, t;scanf("%lf %lf", &v, &t);int wind_chill_index = calculate_wind_chill(v, t);printf("%d\n", wind_chill_index);return 0;
}

风寒指数的样例输出也有问题，120 35 的输出我的输出是37，但是居然能ac，只能说这个题库还是有待打磨

10.颜色模型转换

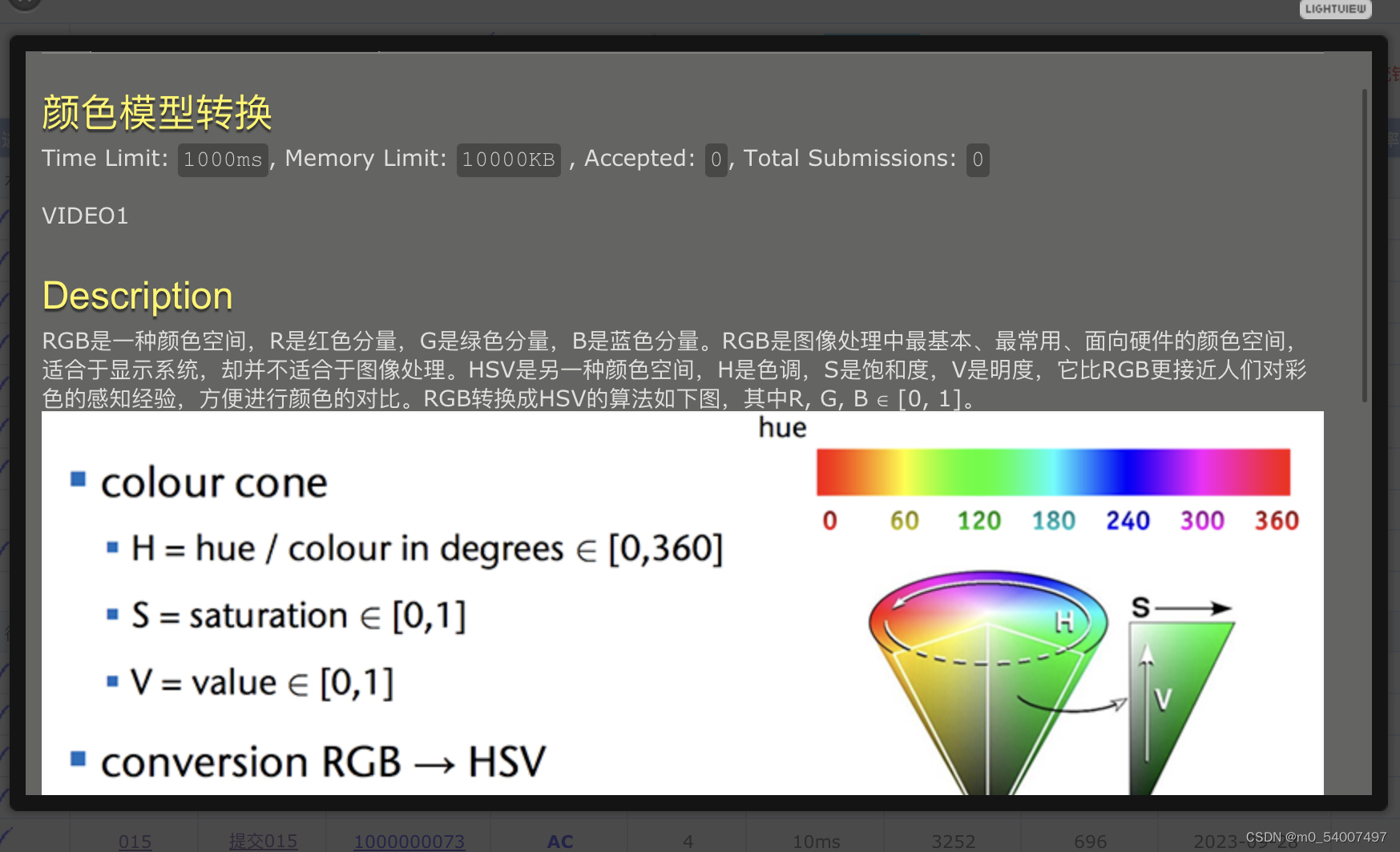
#include<stdio.h>
#include<math.h>
double Max(double a,double b,double c){double temp;if(a>b){temp=a;}else{temp=b;}if(temp>c){return temp;}else return c;}
double Min(double a,double b,double c){double temp;if(a<b){temp=a;}else {temp=b;}if(temp<c){return temp;}else{return c;}
}double rgbtoRGB(double a){return a/(255);
}int main(){double r,g,b,R,G,B;scanf("%lf%lf%lf",&r,&g,&b);R=rgbtoRGB(r);G=rgbtoRGB(g);B=rgbtoRGB(b);double h,s,v;v=Max(R,G,B);if(Max(R,G,B)!=0){s=(Max(R,G,B)-Min(R,G,B))/Max(R,G,B);}if(R==Max(R,G,B)&&Max(R,G,B)-Min(R,G,B)!=0){h=60*((G-B)/(Max(R,G,B)-Min(R,G,B)));}    if(G==Max(R,G,B)&&Max(R,G,B)-Min(R,G,B)!=0){h=60*(2+(B-R)/(Max(R,G,B)-Min(R,G,B)));}if(B==Max(R,G,B)&&Max(R,G,B)-Min(R,G,B)!=0){h=60*(4+(R-G)/(Max(R,G,B)-Min(R,G,B)));}if(h<0){h=h+360;}if(Max(R,G,B)-Min(R,G,B)==0){h=0;}if(Max(R,G,B)==0){s=0;}s=s*100;v=v*100;printf("%.4lf,%.4lf%%,%.4lf%%",h,s,v);
}

注意在转换过程中考虑255 255 255，0，0，0等极端情况

11.操作数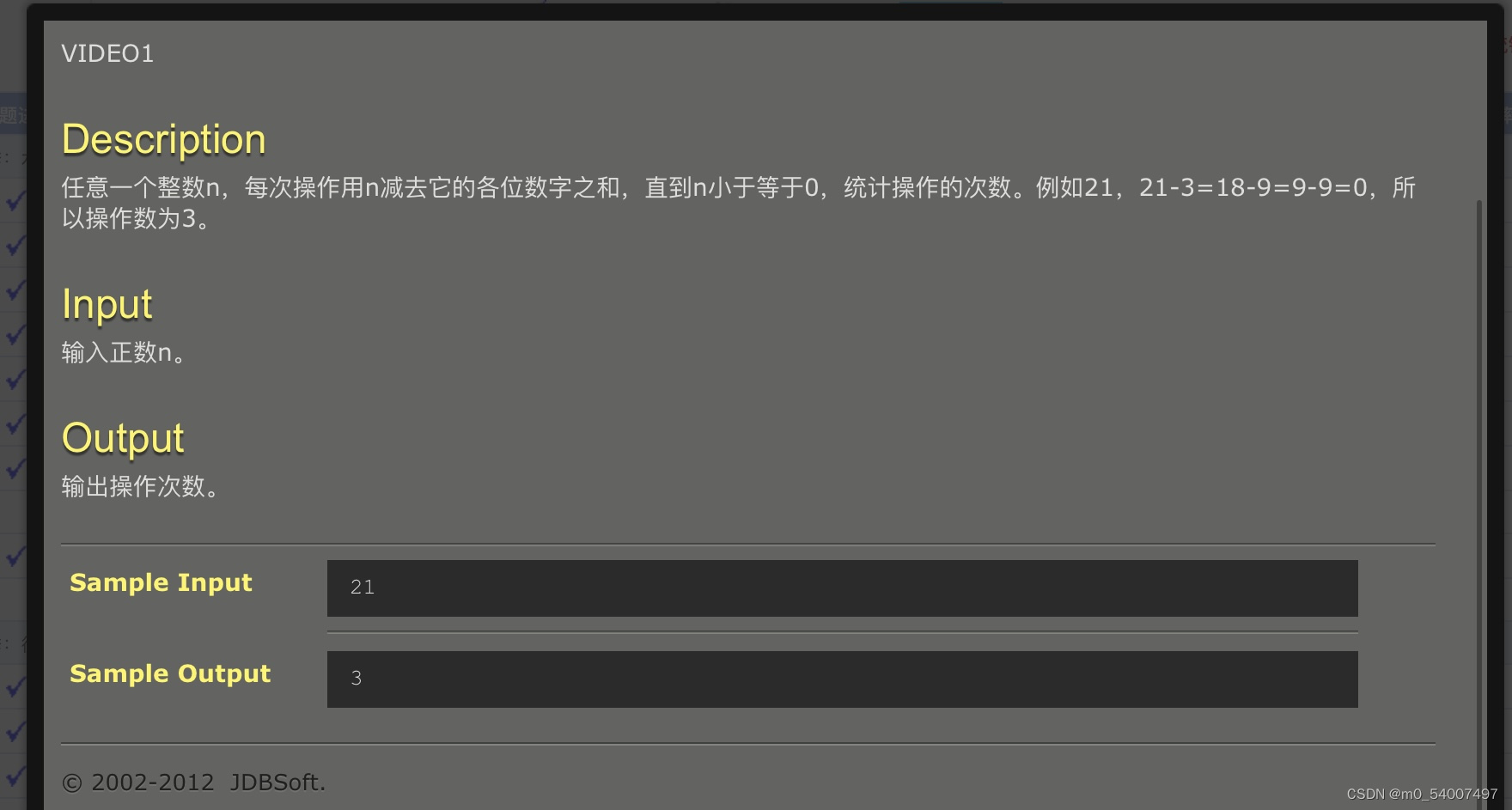

#include <stdio.h>int sum_of_digits(int n) {int sum = 0;while (n > 0) {sum += n % 10;n /= 10;}return sum;
}int main() {int n, count = 0;scanf("%d", &n);while (n > 0) {n -= sum_of_digits(n);count++;}printf("%d\n", count);return 0;
}

12.级数和

#include <stdio.h>
//级数和
double cal(int n) {double sum = 0;double sum2=40.4;if(n<9){   for (int i = 1; i <= n; i++) {printf("%d.%d",i,i+1);sum += (i + (i + 1)*0.1);if(i!=n) printf("+");}return sum;}if(n>=9&&n!=99){printf("1.2+2.3+3.4+4.5+5.6+6.7+7.8+8.9+");for(int m=9;m<=n;m++){if(m%10!=9)printf("%d.%d",m,m+1);else printf("%d.%d",m,(m/10)+1);if(m!=n) printf("+");sum2+=(m+(m+1)*0.01);}return sum2;}if(n==99){cal(98);printf("+99.1");return 5003.55; }}int main() {int n;scanf("%d", &n);double result = cal(n);printf("=%.2lf\n", result);return 0;
}

这个也没有什么特别好说的，注意9.10输出的时候输出9.1这种情况，还要注意分三段讨论，在9和99分成三段，还是输出不好处理，注意即可

13.组合数

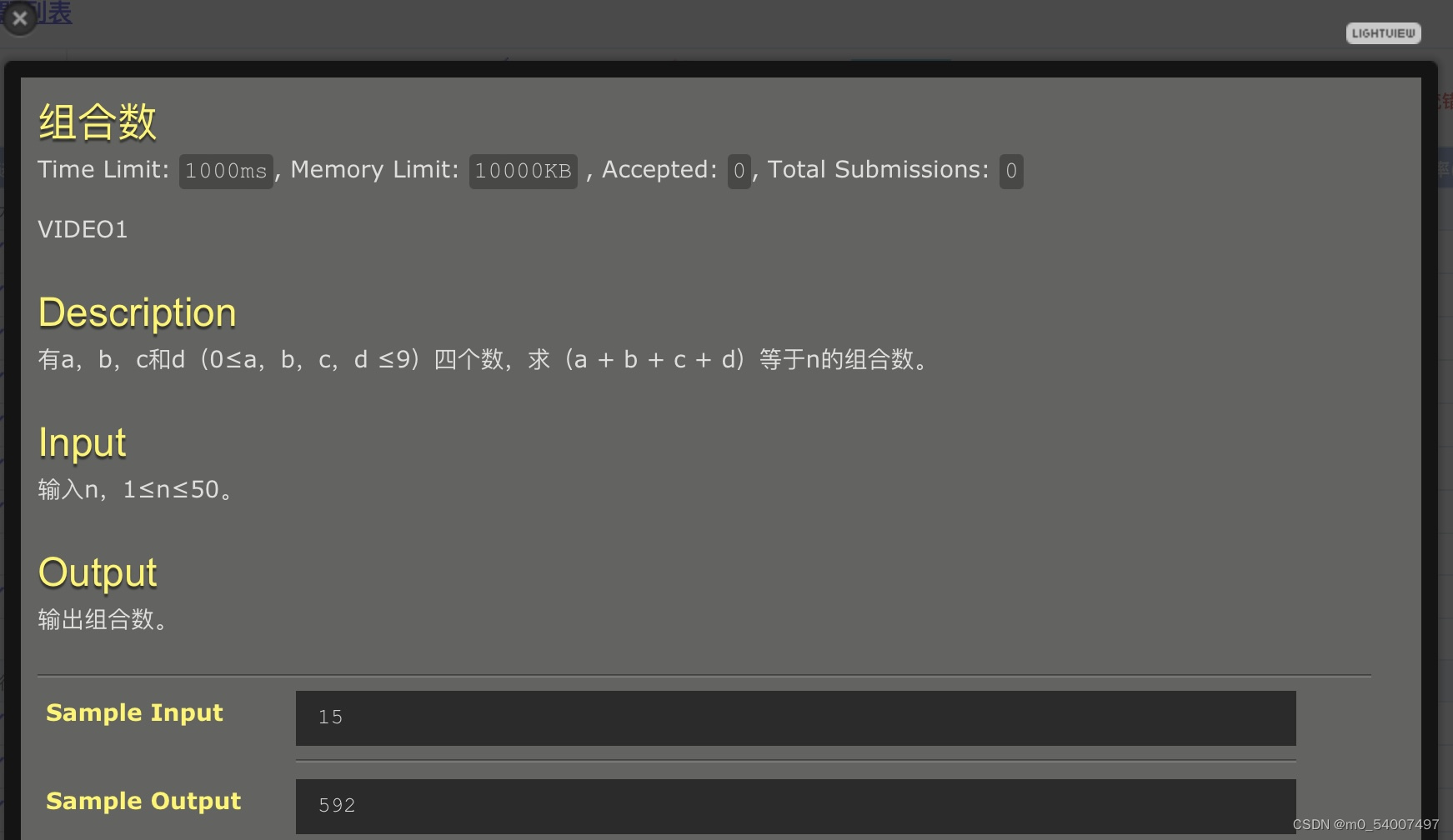
#include<stdio.h>
int count(int a){int arr[5][51]={0};for(int i=0;i<=9;i++){arr[1][i]=1;}for(int j=2;j<=4;j++){for(int m=0;m<=a;m++){for(int n=0;n<=9;n++){if(m>=n){arr[j][m]+=arr[j-1][m-n];}}}}return arr[4][a];
}
int main(){int n;scanf("%d",&n);int result;result =count(n);printf("%d",result);
}

这个是真的重量级，这个是算法课上讲递归和动态规划的例题，可能是输入只有50不需要考虑时间复杂度问题，但是还是在这里简单讲一下动态规划算法

在我的观点看来，动态规划是一种以空间换时间的算法，他将算法的中间值全部存在一个数组中，以此来避免多次重复计算来拖慢算法速度，但是缺点在于他会用一片更大的空间，导致空间复杂度的提升

以这道题为例，我们简单讨论一下这个题目，

先以一个公式来入手 $arr[i][j]=\sum\binom{9}{k=0}arr[i-1][j-k],if j>=k$
这个公式什么含义呢
要计算使用前 i 个数字构成和为 j 的组合数，我们需要考虑前一个数字的组合数。假设前一个数字的值为 k，那么使用前 i 个数字构成和为 j 的组合数，可以分解成两部分：

1.不包含前一个数字 k 的组合数，也就是使用前 i-1 个数字构成和为 j 的组合数，即 dp[i-1][j]。

2.包含前一个数字 k 的组合数，也就是使用前 i-1 个数字构成和为 j-k 的组合数，即 dp[i-1][j-k]。

所以，通过对所有可能的 k 值进行求和，就能得到使用前 i 个数字构成和为 j 的所有组合数。

利用这个公式可以将整个数组初始化完成，当然，这个题目的范围很小，我们也可以使用递归的方法来解决

#include <stdio.h>int count(int i, int j) {if (i == 1) {if (j >= 0 && j <= 9) {return 1; // 初始化条件：只用一个数字构成和为j的组合数为1} else {return 0; // 其他情况下，返回0}}int total = 0;for (int k = 0; k <= 9; k++) {if (j >= k) {total += count(i - 1, j - k);}}return total;
}int main() {int n;scanf("%d", &n);int result = count(4, n);printf("%d\n", result);return 0;
}

递归的优点在于所占空间小，但是会有更长的耗时，如果在算法课程中对这类题使用递归很有可能出现超时的情况

14.方阵

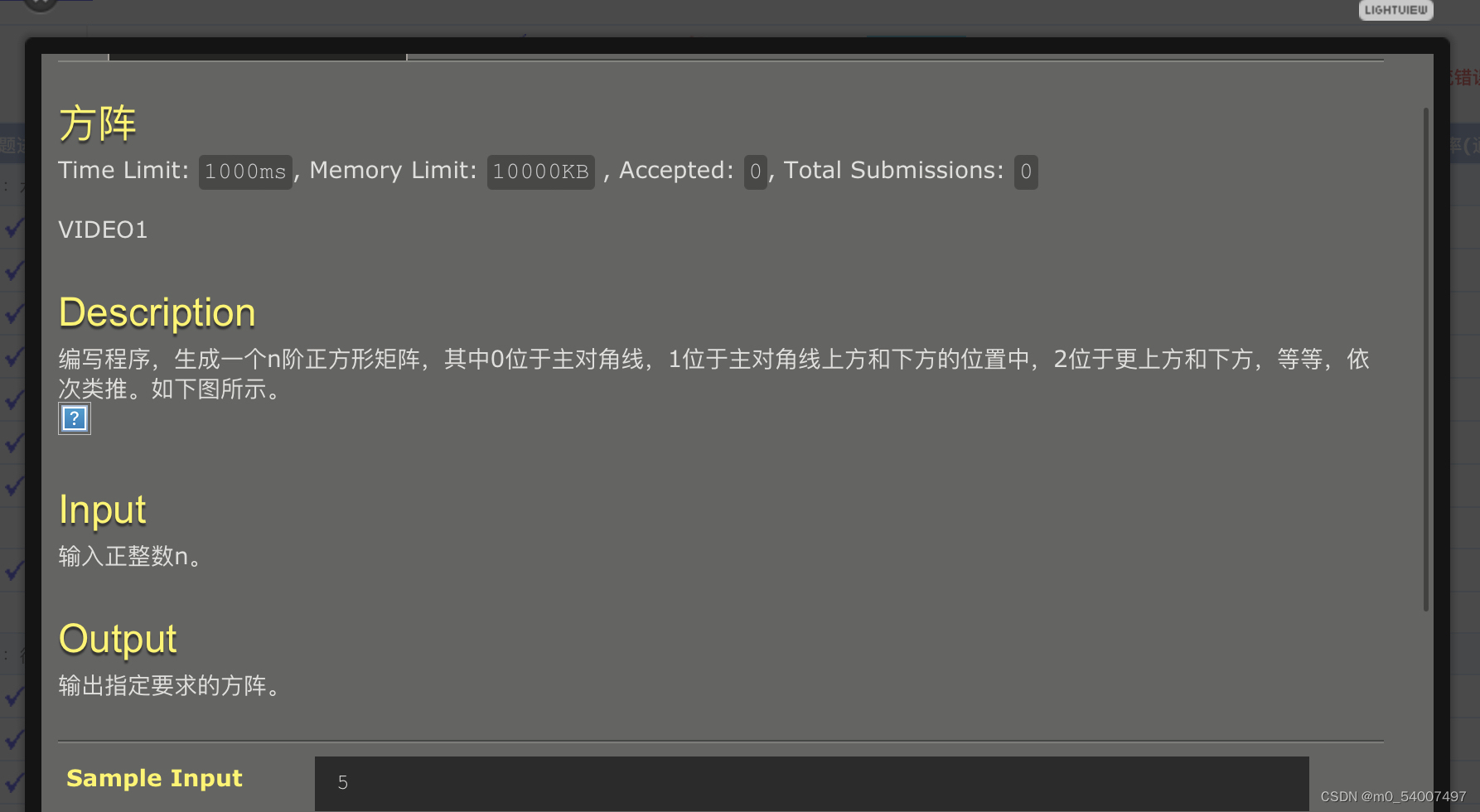
#include<iostream>
using namespace std;
long long int max(long long int a,long long int b)
{return a>=b?a:b;    
}
long long int min(long long int a, long long int b)
{return a<=b?a:b;
}
int main()
{long long int n;cin>>n;for(long long int i=1;i<=n;i++){for(long long int j=1;j<=n;j++){long long int t=max(i,j)-min(i,j);cout<<t;if(j!=n) cout<<"  ";}if(i!=n)cout<<endl;}
}

这个题目要求输出一个方阵，我们以数组表示，则不难发现a[n][n]=0,a[n][n+1]=1......通过找规律我们可以发现每一个元素都是a[i][j]中较大的减去较小的数，输出即可，注意的是输出的方阵没两个数之间有两个空格，这个导致我wa了很多次调试了很多次。

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int main(){int ** a;int length;int high;scanf("%d",&high);length=high;a=(int **)malloc(length*sizeof(int *));for(int i=0;i<length;i++){a[i]=(int *)malloc(high *sizeof(int ));}for(int i=0;i<length;i++){for(int j=0;j<high;j++){a[i][j]=fabs(i-j);if(j!=high-1) printf("%d ",a[i][j]);else{printf("%d",a[i][j]);}}printf("\n");}
}

更新过一次题目，这个是现在可以用的答案，

15.比率

#include<stdio.h>
long long int gcd(long long int a,long long int b){while(b!=0){int temp=b;b=a%b;a=temp;}return a;}
int float_to_fraction(double num){long long Big=1e9;if(num==0){printf("0");return 0;}if(num<0){printf("-");num=-num;}long long num1=num*Big;long long  big =Big;//用一个很大的数将浮点数转为整数long long comgcd=gcd(num1,big);num1 /=comgcd;big /= comgcd;printf("%lld/%lld",num1,big);}int main(){double num;scanf("%lf",&num);float_to_fraction(num);return 0;
}

如何将一个小数转换成比率，我们不妨使用一个很大的数字，例如1e9，将其变成一个整数/大数的形式，然后利用辗转相除法找到公因数，最后得到结果，值的注意的是这道题要考虑0和负数的情况。

16.乘数模

#include <stdio.h>unsigned long long fast_mod_multiply(unsigned long long a, unsigned long long b, unsigned long long m) {unsigned long long result = 0;a = a % m;while (b > 0) {if (b % 2 == 1) {result = (result + a) % m;}a = (a * 2) % m;b = b / 2;}return result;
}int main() {unsigned long long a, b, m;scanf("%llu", &a);scanf("%llu", &b);scanf("%llu", &m);unsigned long long result = fast_mod_multiply(a, b, m);printf("%llu\n",result);return 0;
}

快速模乘法，csdn上有详细解释，不多赘述

17.对称数

#include<stdio.h>
int GetFigure(int a){int count=0;do{count++;a/=10;}while(a!=0);{return count;   }
}//获取一个数字有几位
void GetFigureToStorage(int a,int arr[],int b){for(int i=0;i<b;i++){arr[i]=a%10;a/=10;}}//获取一个数字的各个位数,并存在数组里
int YesOrNo(int arr[],int a){int count=0;if(a%2==1){if(arr[(a+1)/2-1]==1||arr[(a+1)/2-1||arr[(a+1)/2-1]==8]==0){for(int i=0;i<a;i++){if(arr[i]==6&&arr[a-i-1]==9){{count++;}}if(arr[i]==9&&arr[a-i-1]==6){count++;}if(arr[i]==1){count++;}if(arr[i]==0){count++;}if(arr[i]==8){count++;}count++;}}}if(a%2==0){for(int j=0;j<a;j++){if(arr[j]==6&&arr[a-j-1]==9){{count++;}}if(arr[j]==9&&arr[a-j-1]==6){count++;}if(arr[j]==1){count++;}if(arr[j]==0){count++;}if(arr[j]==8){count++;}}}return count;
}
int main(){int a;int arr1[32];int flag=0;scanf("%d",&a);int b;b=GetFigure(a);GetFigureToStorage( a, arr1, b);int m;m=YesOrNo(arr1,b);if((b%2==0&&m==b)||(b%2==1&&m==2*b)){printf("Yes");}else{printf("No");}}

我的方法是将每一位都存在一个数组之中，通过判断每一位是否是对称数的情况来判断整个数字是否是对称数，对称数的要求是6和9必须在对称的位置上，其他位必须是1 0 8，通过判断每一位的方法就能得到对称数是否满足。

18.倍数和

#include <stdio.h>int getMultiplesSum(int n) {int sum = 0;for (int i = 1; i < n; i++) {if (i % 3 == 0 || i % 5 == 0) {sum += i;}}return sum;
}int main() {int T;scanf("%d", &T);int arr[1000000];for (int i = 0; i < T; i++) {int n;scanf("%d", &n);int result = getMultiplesSum(n);arr[i]=result;}for (int m=0;m<T;m++){printf("%d\n",arr[m]);}return 0;
}

通过判断是否是3和5的倍数将其递增，很基础的一道题

19.幂数模

#include<bits/stdc++.h>
using namespace std;
long long Mode(long long a, long long b, long long mode)
{long long sum = 1;while (b) {if (b & 1) {sum = (sum * a) % mode;b--;}b /= 2;a = a * a % mode;}cout<<sum;return 0;
}
int main()
{long long int a,b,c;cin>>a>>b>>c;Mode(a,b,c);
}

快速幂模算法，csdn上有详细说明，可以自己去看

20.分数的加、减、乘、除法

#include <stdio.h>// 辗转相除法求最大公约数
int gcd(int a, int b) {while (b != 0) {int temp = b;b = a % b;a = temp;}return a;
}// 结构体表示分数
typedef struct {int numerator; // 分子int denominator; // 分母
} Fraction;// 将分数化简为最简分数形式
void simplify_fraction(Fraction *frac) {int common_divisor = gcd(frac->numerator, frac->denominator);frac->numerator /= common_divisor;frac->denominator /= common_divisor;
}int main() {Fraction frac1, frac2;// 输入第一个分数scanf("%d/%d", &(frac1.numerator), &(frac1.denominator));// 输入第二个分数scanf("%d/%d", &(frac2.numerator), &(frac2.denominator));// 加法Fraction sum;sum.numerator = frac1.numerator * frac2.denominator + frac2.numerator * frac1.denominator;sum.denominator = frac1.denominator * frac2.denominator;simplify_fraction(&sum);// 减法Fraction diff;diff.numerator = frac1.numerator * frac2.denominator - frac2.numerator * frac1.denominator;diff.denominator = frac1.denominator * frac2.denominator;simplify_fraction(&diff);// 乘法Fraction product;product.numerator = frac1.numerator * frac2.numerator;product.denominator = frac1.denominator * frac2.denominator;simplify_fraction(&product);// 除法Fraction quotient;quotient.numerator = frac1.numerator * frac2.denominator;quotient.denominator = frac1.denominator * frac2.numerator;simplify_fraction(&quotient);// 输出结果printf("(%d/%d)+(%d/%d)=%d/%d\n", frac1.numerator, frac1.denominator, frac2.numerator, frac2.denominator, sum.numerator, sum.denominator);printf("(%d/%d)-(%d/%d)=%d/%d\n", frac1.numerator, frac1.denominator, frac2.numerator, frac2.denominator, diff.numerator, diff.denominator);printf("(%d/%d)*(%d/%d)=%d/%d\n", frac1.numerator, frac1.denominator, frac2.numerator, frac2.denominator, product.numerator, product.denominator);printf("(%d/%d)/(%d/%d)=%d/%d\n", frac1.numerator, frac1.denominator, frac2.numerator, frac2.denominator, quotient.numerator, quotient.denominator);return 0;
}

难点在于辗转相除法求最大公因数，其他的难点不多，只是麻烦，我是用gpt生成的代码，不过很显然这个题gpt的方法有点过于麻烦了，但是能ac就行

21.倒水

#include<stdio.h>struct createqueue {int a,b;
};
createqueue queue[10000];
int head,tail;
int chongfu[1000][1000];
int tag;
void in(int n,int m) {queue[tail].a=n,queue[tail].b=m;tail++;
}
int out(int i) {if(i==1)return queue[head].a;else if(i==2)return queue[head].b;
}
int count;
int maxn,maxm,result;
void bfs() {int n=out(1),m=out(2);int t=chongfu[n][m];//printf("%d%d\n",n,m);head++;if(n==result||m==result) {printf("%d",t-1);tag=1;}for(int i=0; i<=5; i++) {switch(i){case 0: {if(!chongfu[n][0]) {in(n,0);chongfu[n][0]=t+1;};break;}case 1: {if(!chongfu[0][m]) {in(0,m);chongfu[0][m]=t+1;break;}}case 2: {if(!chongfu[maxn][m]) {in(maxn,m);chongfu[maxn][m]=t+1;}break;}case 3: {if(!chongfu[n][maxm]) {in(n,maxm);chongfu[n][maxm]=t+1;}break;}case 4: {if(n+m>=maxm&&(!chongfu[n+m-maxm][maxm])) {in(n+m-maxm,maxm);chongfu[n+m-maxm][maxm]=t+1;}if(n+m<maxm&&(!chongfu[0][n+m])) {in(0,n+m);chongfu[0][n+m]=t+1;}break;}case 5: {if(n+m>=maxn&&(!chongfu[maxn][m+n-maxn])) {in(maxn,m+n-maxn);chongfu[maxn][m+n-maxn]=t+1;}if(n+m<maxn&&(!chongfu[m+n][0])) {in(m+n,0);chongfu[m+n][0]=t+1;break;}}}}
}int main() {scanf("%d%d%d",&maxn,&maxm,&result);in(0,0);chongfu[0][0]=1;while(head!=tail) {bfs();if(tag==1){//printf("success!\n");return 0;}}//printf("failed!");}

bfs做的，不使用bfs的做法ac不了。

22.方案数

#include <stdio.h>int countWays(int N) {int count = 0;for (int i = 1; i <= N/2; i++) {int currentSum = i;int j = i + 1;while (currentSum < N) {currentSum += j;j++;}if (currentSum == N) {count++;}}return count + 1; // 加上N本身作为一种方案
}int main() {int N;scanf("%d", &N);int result = countWays(N);printf("%d\n", result);return 0;
}

个人觉得很简单

23.好数字

#include <iostream>
using namespace std;#define MOD 1000000007long long quick_mul(int x, long long N)
{long long res = 1;long long x_contribute = x;while (N > 0) {if (N % 2 == 1) {res = res * x_contribute % MOD;}x_contribute = x_contribute * x_contribute % MOD;N /= 2;}return res;
}int countGoodNumbers(long long n)
{return quick_mul(5, n - n / 2) * quick_mul(4, n / 2) % MOD;
}int main()
{long long n;// 获取用户输入cin >> n;// 调用 countGoodNumbers 函数int result = countGoodNumbers(n);// 输出结果cout << result << endl;return 0;
}

类似于排列组合的一道题，给定奇数位和偶数位，然后自己排列组合看有多少种可能性

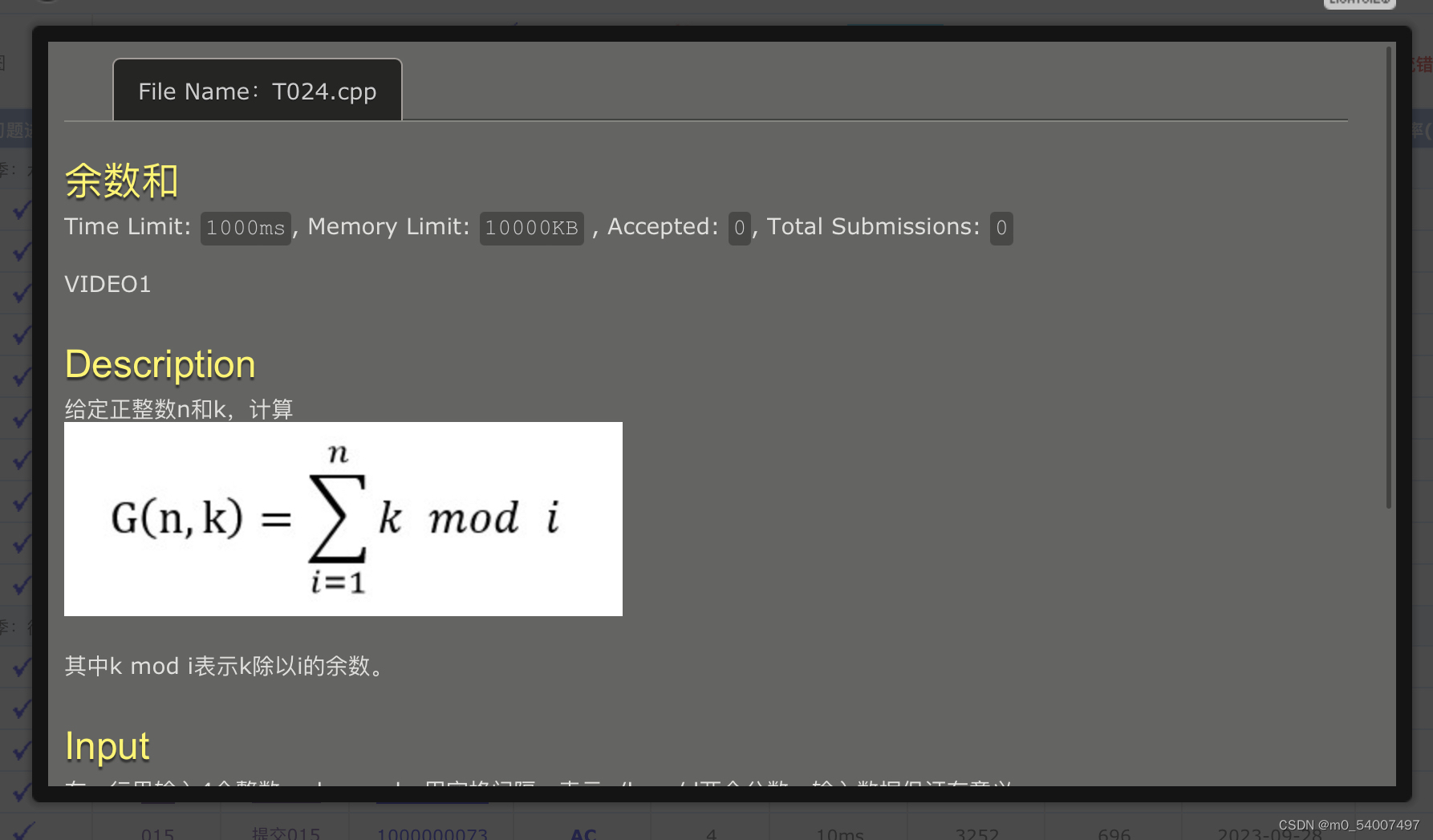
24.余数和

#include<stdio.h>
int sum(int n,int k){int sum=0;for(int i=1;i<=n;i++){sum=sum+k%i;}return sum;
}
int main(){int a,b;scanf("%d%d",&a,&b);printf("%d",sum(a,b));
}

记录余数然后求和，比较简单

25.最大数字

#include<stdio.h>
void GetFigureToStorage(int a,int arr[],int b){for(int i=0;i<b;i++){arr[i]=a%10;a/=10;}}//获取一个数字的各个位数,并存在数组里
int GetFigure(int a){int count=0;do{count++;a/=10;}while(a!=0);{return count;   }
}//获取一个数字有几位
int isincrease(int a){int b=GetFigure(a);int arr[32];int count=0;GetFigureToStorage(a,arr,b);for(int i=0;i<b-1;i++){if(arr[i+1]-arr[i]>0){count++;}}if(count==0){return 1;}else{return 0;}
}
int main(){int a;scanf("%d",&a);int i=a;if(i<10){printf("%d",i);}if(i==10){printf("9");}if(i==11){printf("9");}if(i>=12){while(1){if(isincrease(i)==1){printf("%d",i);break;}i--;}}
}

我的算法是从给定的数开始，判断其是否为所需数字，否则就减一继续判断，缺点在于时间复杂度过高，这个题的测试样例很显然没有很恶心人的，所以能通过，但是依然存在时间复杂度过高的情况，最好还是用贪心写

26.查找数列

#include <stdio.h>int findNumber(int n) {int current = 1; // 初始值为1int i, j;for (i = 1; i <= n; i++) {for (j = 1; j <= i; j++) {if (current == n) {return j;}current++;}}return -1; // 如果未找到，返回-1
}int main() {int n;scanf("%d", &n);int result = findNumber(n);printf("%d\n",result);return 0;
}

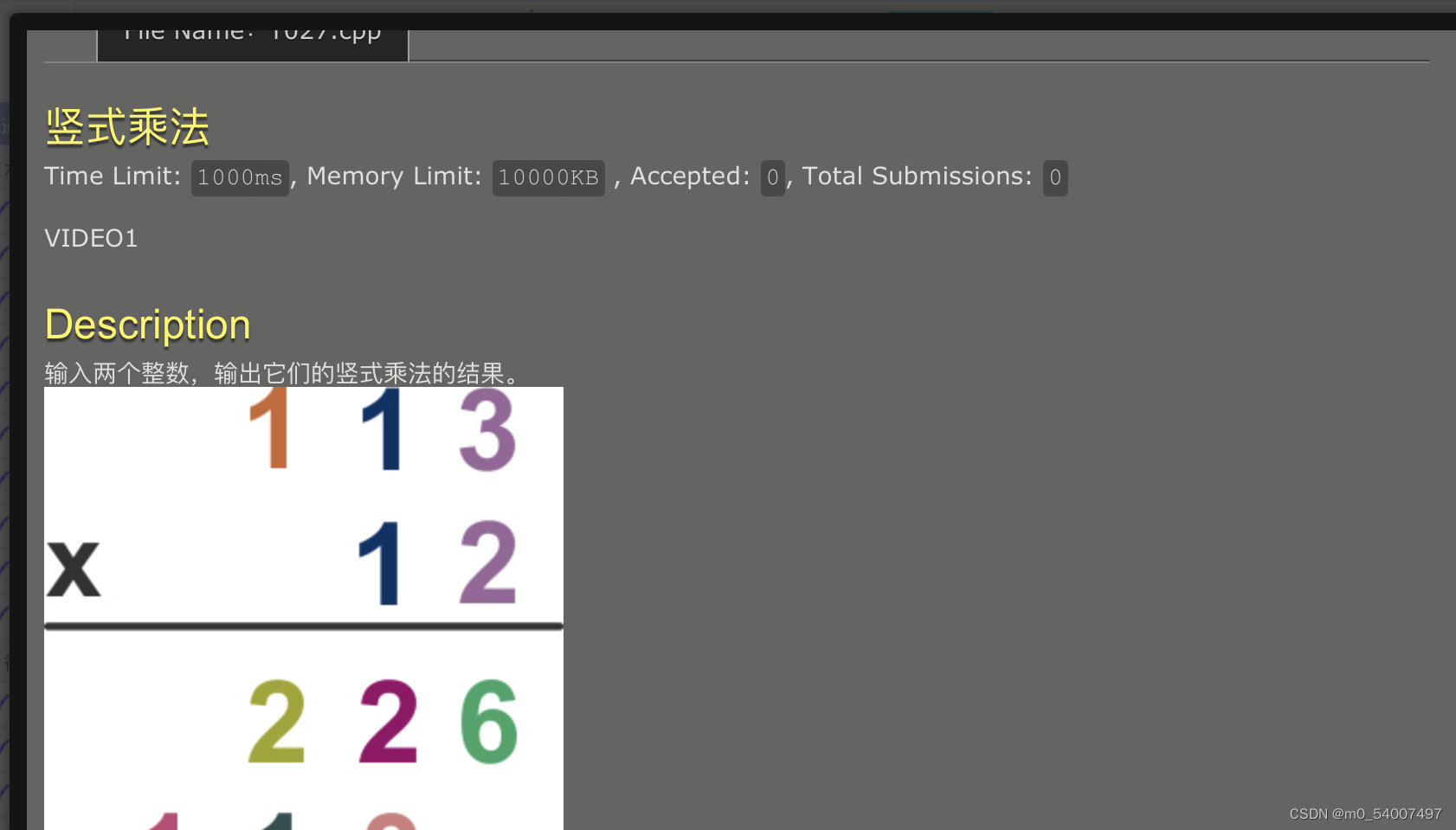
27.竖式计算

#include<stdio.h>
int GetFigure(int a){int count=0;do{count++;a/=10;}while(a!=0);{return count;}
}//获取一个数字有几位
void GetFigureToStorage(int a,int arr[],int b){for(int i=0;i<b;i++){arr[i]=a%10;a/=10;}
}//获取一个数字的各个位数,并存在数组里
void figuermti(int arr[],int a,int c,int e){int arr1[32];int count;for(int i=0;i<c;i++){arr1[i]=arr[i]*a;}count=GetFigure(arr1[c-1])+c;for(int m=0;m<count-GetFigure(a);m++){printf(" ");}printf("%d\n",a);printf("x");for(int n=0;n<count-GetFigure(e)-1;n++){printf(" ");}printf("%d\n",e);for(int n=0;n<count;n++){printf("-");}printf("\n");//前3行for(int i=0;i<c-1;i++){for(int m=0;m<count-GetFigure(arr1[i])-i;m++) {printf(" ");}printf("%d",arr1[i]);if(i==0){printf("\n");}else {for(int n=0;n<i;n++){printf(" ") ;}printf("\n");}}printf("+");printf("%d",arr1[c-1]);for(int i=0;i<c-1;i++){printf(" ");}printf("\n");for(int n=0;n<count;n++){printf("-");}printf("\n");for(int m=0;m<count-GetFigure(a*e);m++){printf(" ");}printf("%d",a*e);}
int main(){int a,b,c;scanf("%d%d",&a,&b);int arr[32];c=GetFigure(b);GetFigureToStorage(b,arr,c);figuermti(arr,a,c,b);}

计算五分钟，排版两小时

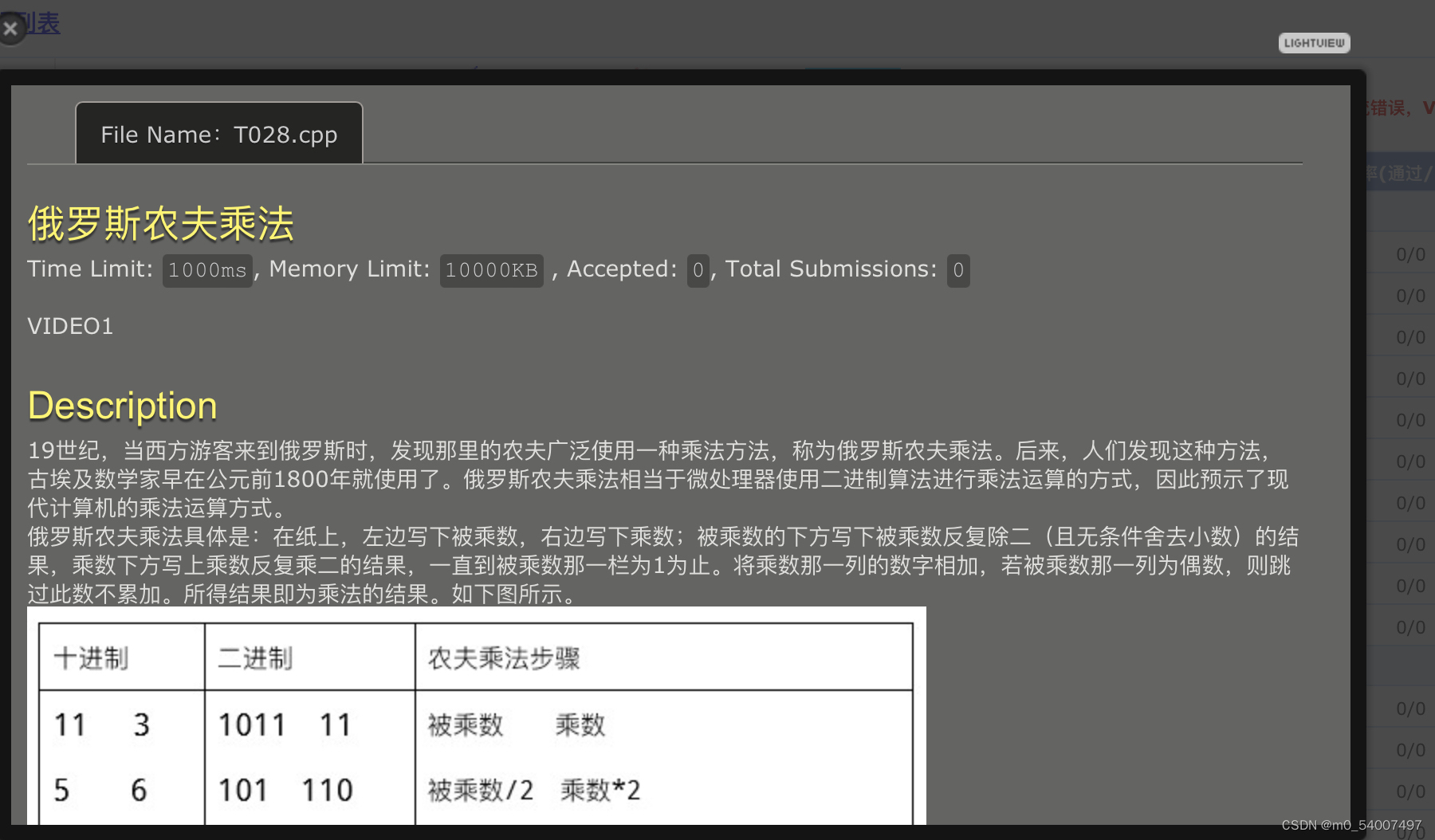
28.俄罗斯农夫乘法

#include <stdio.h>int Mul(int m, int n)
{int sum = 0, a = 0;if (n == 0 || m == 0)return 0;if (n == 1)return m;printf("%d %d\n", n, m); // 输出当前的 n 和 mwhile (n != 1){if (n % 2 == 0){n = n / 2;m *= 2;}else{n = n / 2;a += m;m *= 2;}printf("%d %d\n", n, m); // 输出当前的 n 和 m}sum = a + m;return sum;
}int main()
{int m, n; // 两个相乘的数int sum = 0;scanf("%d %d", &m, &n);sum = Mul(n, m);printf("%d\n", sum);return 0;
}

利用题给的算法计算输出即可

29.阶乘倍数

#include<iostream>
using namespace std;
#define mem(a,b) memset(a,b,sizeof(a))
#define pb push_back
const int INF = 1e21;
typedef long long ll;
const int maxn = 1e4 + 7;
long long int t,p;
bool isPrime(int p){if(p == 1) return false;for (int i = 2; i*i <= p; i++) {if(p % i == 0) return false;}return true;
}
int gcd(int a,int b){if(b == 0) return a;return gcd(b,a%b);
}
int main(){cin>>p;if (p == 1 || isPrime(p)) {cout<<p;}else{for (int i = 2; ; i++) {if (gcd(i,p) != 1) {p /= gcd(i,p);if (p == 1) {cout<<i;break;}if (i < p && isPrime(p)) {cout<<p;break;}}}}
return 0;
}

https://blog.csdn.net/weixin_35105950/article/details/117115648?app_version=6.1.7&csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22117115648%22%2C%22source%22%3A%22m0_54007497%22%7D&utm_source=app

30.毕达哥拉斯三元组

#include <stdio.h>void findPythagoreanTriplets(int n) {int a, b, c;int found = 0;for (a = 1; a <= n; a++) {for (b = a; b <= n; b++) {c = n - a - b;if (c >= b && a*a + b*b == c*c) {printf("%d\n", a * b * c);found = 1;break;}}if (found == 1) {break;}}if (found == 0) {printf("没有找到满足条件的三个数字。\n");}
}int main() {int n;scanf("%d", &n);findPythagoreanTriplets(n);return 0;
}

找到这三个数然后算乘积即可。

31.基思数

#include <stdio.h>int arr[8] = {0};int init(int n){int cnt = 0;while (n) {arr[cnt++] = n%10;n /= 10;}return cnt;
}void isKeith(int n, int len){int i = len - 1;while (arr[i] < n){int sum = 0;for (int j = 0; j < len; ++j) {sum += arr[(i-j+len)%len];}arr[i] = sum;i = (i-1+len)%len;}if (arr[i] == n) printf("Yes");else printf("No");
}int main() {int n;scanf("%d",&n);isKeith(n,init(n));return 0;
}

这道题我不知道为什么不能ac

这里采用了另一位同学@annesede的答案，

http://【2023西工大NOJ (C语言版) 持续更新ing - CSDN App】http://t.csdnimg.cn/tD4CV

我本人的做法也放在这里,但是不能ac

#include<stdio.h>
int GetFigure(int a){int count=0;do{count++;a/=10;}while(a!=0);{return count;}
}//获取一个数字有几位
void GetFigureToStorage(int a,int arr[],int b){for(int i=b-1;i>=0;i--){arr[i]=a%10;a/=10;}
}//获取一个数字的各个位数,并存在数组里
int main(){int a,flag;flag=0;scanf("%d",&a);int arr[30];int length=GetFigure(a);GetFigureToStorage( a,arr,length);for(int i=length;i<30;i++){for(int j=1;j<=length;j++){arr[i]+=arr[i-j];            }    }for(int m=0;m<30;m++){if(a==arr[m]){printf("Yes");flag=1;break;}}if(flag==0){printf("No");}
}

#include<stdio.h>
int main(){long long arr[55]={14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, 31331, 34285, 34348, 55604, 62662, 86935, 93993, 120284, 129106, 147640, 156146, 174680, 183186, 298320, 355419, 694280, 925993, 1084051, 7913837, 11436171, 33445755, 44121607, 129572008, 251133297, 24769286411, 96189170155, 171570159070, 202366307758, 239143607789, 296658839738, 1934197506555, 8756963649152, 43520999798747, 74596893730427, 97295849958669, 120984833091531, 270585509032586, 754788753590897};long long a;int b=0;scanf("%lld",&a);for(int i=0;i<55;i++){if(arr[i]==a){printf("Yes");b=1;}}if(b==0){printf("No");}
}

32.哈沙德数

#include <stdio.h>int HarshadNumber(int n){int t = n, s = 0;while (t) {s += t % 10;t /= 10;}if ((s == 0) || (n % s != 0)) return 0;if (s == 1) return 1;return n / s;
}int main(){int a;int count=0;scanf("%d", &a);if (a == 1) {count = 1;}while ((a != 0) && (a != 1)) {a= HarshadNumber(a);if (a) {count++;}}printf("%d", count);return 0;
}

出题人给了函数，调用即可

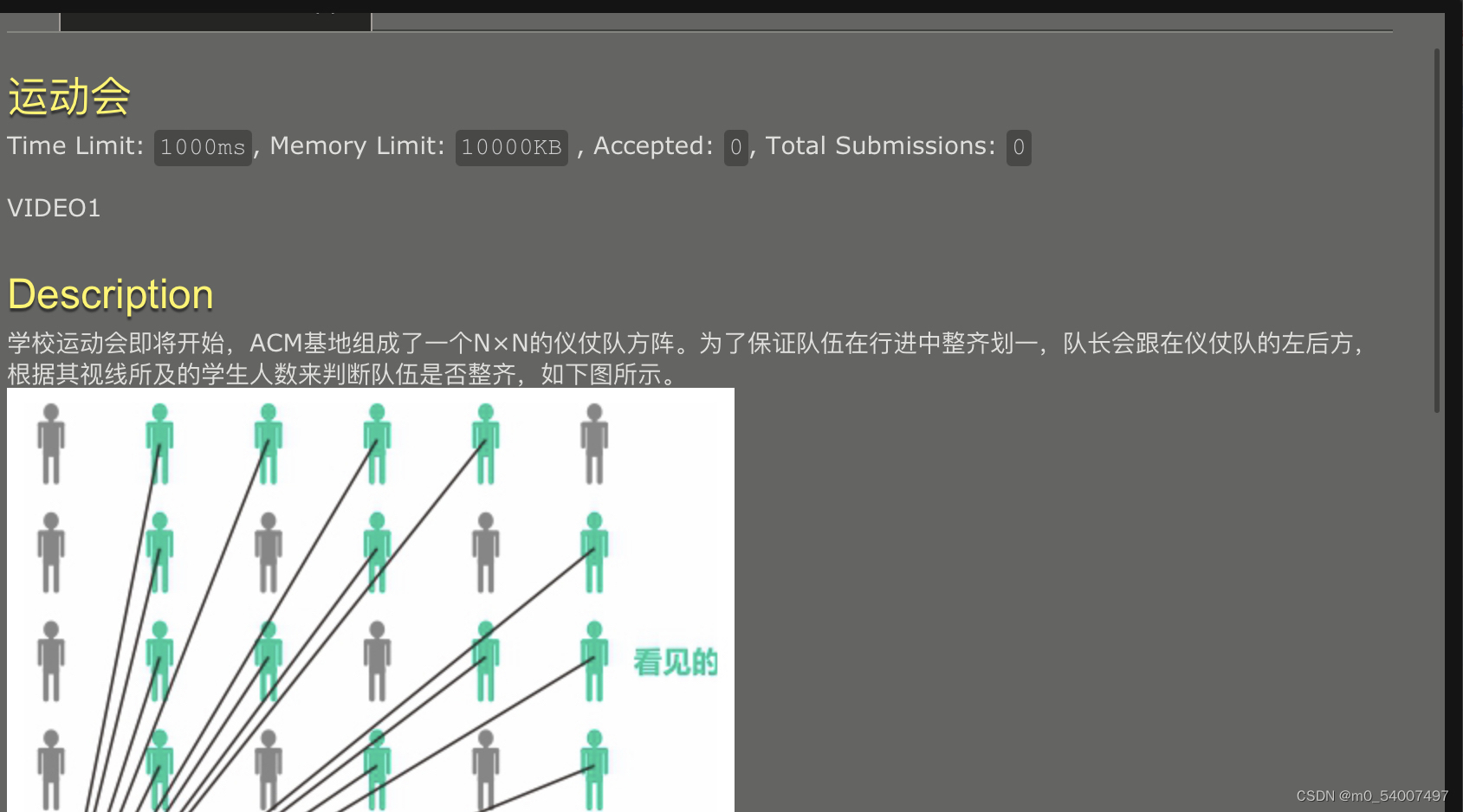
33.运动会

#include <bits/stdc++.h>
#define MAXN 40000 + 10int phi[MAXN],ans[MAXN];void euler()
{ans[1] = 1;for (int i = 1; i <= MAXN; i++){int res = i, n = i;for (int j = 2; j * j <= n; j++){if (!(n % j))res = res * (j - 1) / j;while (!(n % j))n /= j;}if (n > 1)res = res * (n - 1) / n;phi[i] = res;}for (int i = 2; i <= MAXN; i++)for (int j = 1; j < i; j++)ans[i] += phi[j];
}int main(int argc, char const *argv[])
{euler();int n;while (~scanf("%d", &n)){if (n == 1) //方阵大小为1*1时特判，此时队列中只有自己，输出0{puts("0");continue;}printf("%d\n", 2 * ans[n] + 1);}return 0;
}

这里其实是看每一个人所在的x,y是否互质；但是我采用的方法时间复杂度过高te了几次也懒得改了，就采用了别人写好的，连接如下http://【P2158 [SDOI2008]仪仗队题解 - CSDN App】http://t.csdnimg.cn/osuME

34.可变参数平均

#include<stdio.h>
#include<stdarg.h>
double avg(int count,...){
va_list args;
va_start(args,count);
double sum=0;
double avg;
for(int i=0;i<count;i++){int num=va_arg(args,double);sum=sum+num;
}
avg=sum/count;
return avg;
}
int main(){double avg1;double a,b,c,d,e;scanf("%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e);avg1=avg(2,a,b)-avg(3,c,d,e);printf("%.4lf",avg1);
}

这个问题读懂stdarg.h如何使用即可，还算简单

35.可变参数累加

#include <stdio.h>
#include <stdarg.h>int sum(int first, ...) {int result = first;va_list args;va_start(args, first);int num;while ((num = va_arg(args, int)) > 0) {result += num;}va_end(args);return result;
}int main() {int a, b, c, d, e, f;scanf("%d %d %d %d %d %d", &a, &b, &c, &d, &e, &f);int result = sum(a, b, 0) - sum(c, d, e, f, 0);printf("%d", result);return 0;
}

类似上个题目

36.二进制表示

#include <stdio.h>void binary_expression(int n) {if (n == 0) {return;}if (n == 1) {printf("2(0)");return;}if (n == 2) {printf("2");return;}int k = 0;while ((1 << (k + 1)) <= n) {k++;}if (k == 1) {printf("2");} else {printf("2(");binary_expression(k);printf(")");}if (n - (1 << k) != 0) {printf("+");binary_expression(n - (1 << k));}
}int main() {int n;scanf("%d", &n);binary_expression(n);return 0;
}

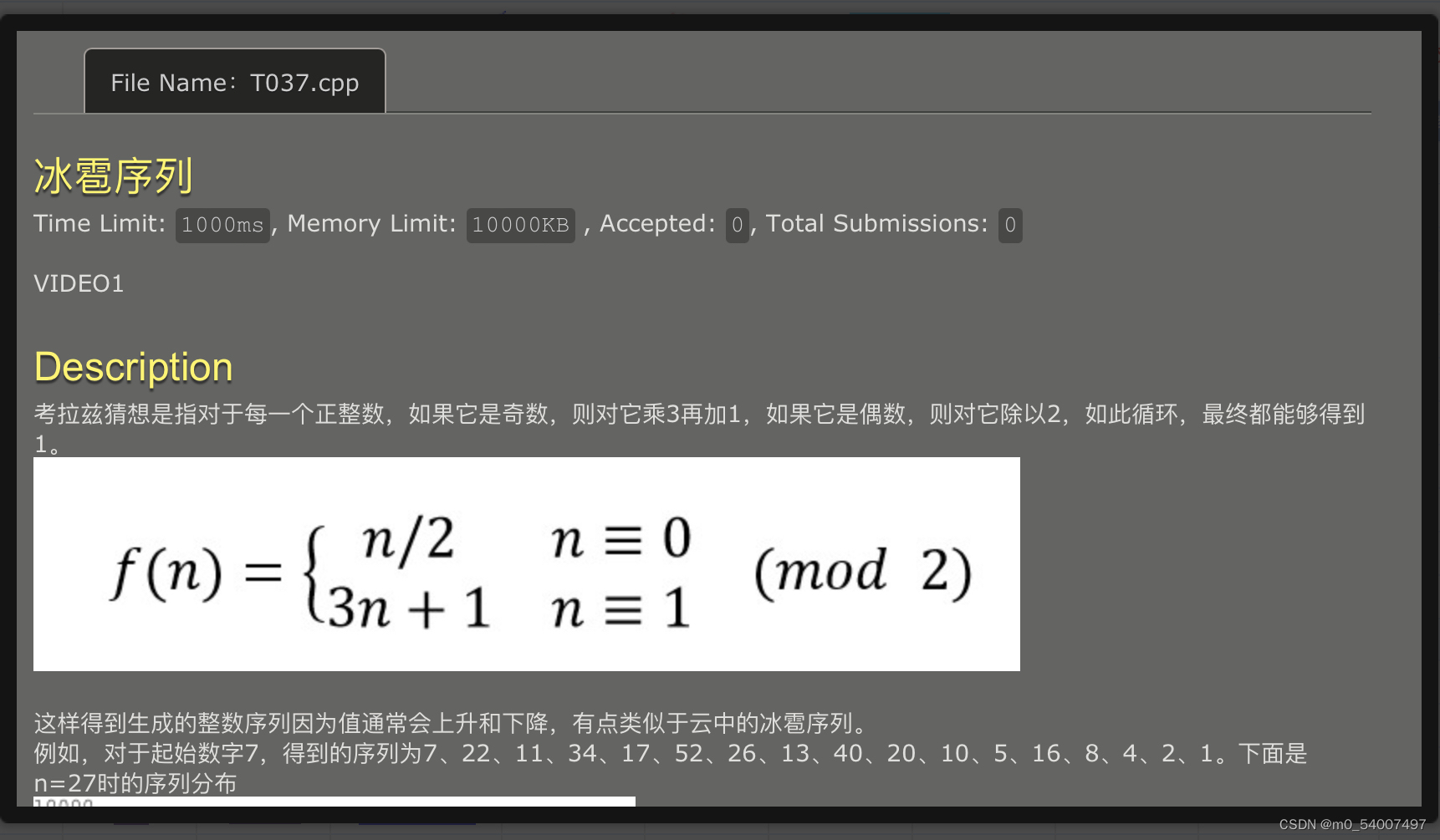
37.冰雹序列

#include<stdio.h>
int fun(int a){if(a%2==0){a=a/2;if(a!=1){printf("%d ",a);}}if(a%2==1&a!=1){a=a*3+1;if(a!=1){printf("%d ",a);}}if(a==1){return 1;}return fun(a);
}
int main(){int a;scanf("%d",&a);printf("%d ",a);fun(a);printf("1");
}

很简单的递归

38.光线追踪

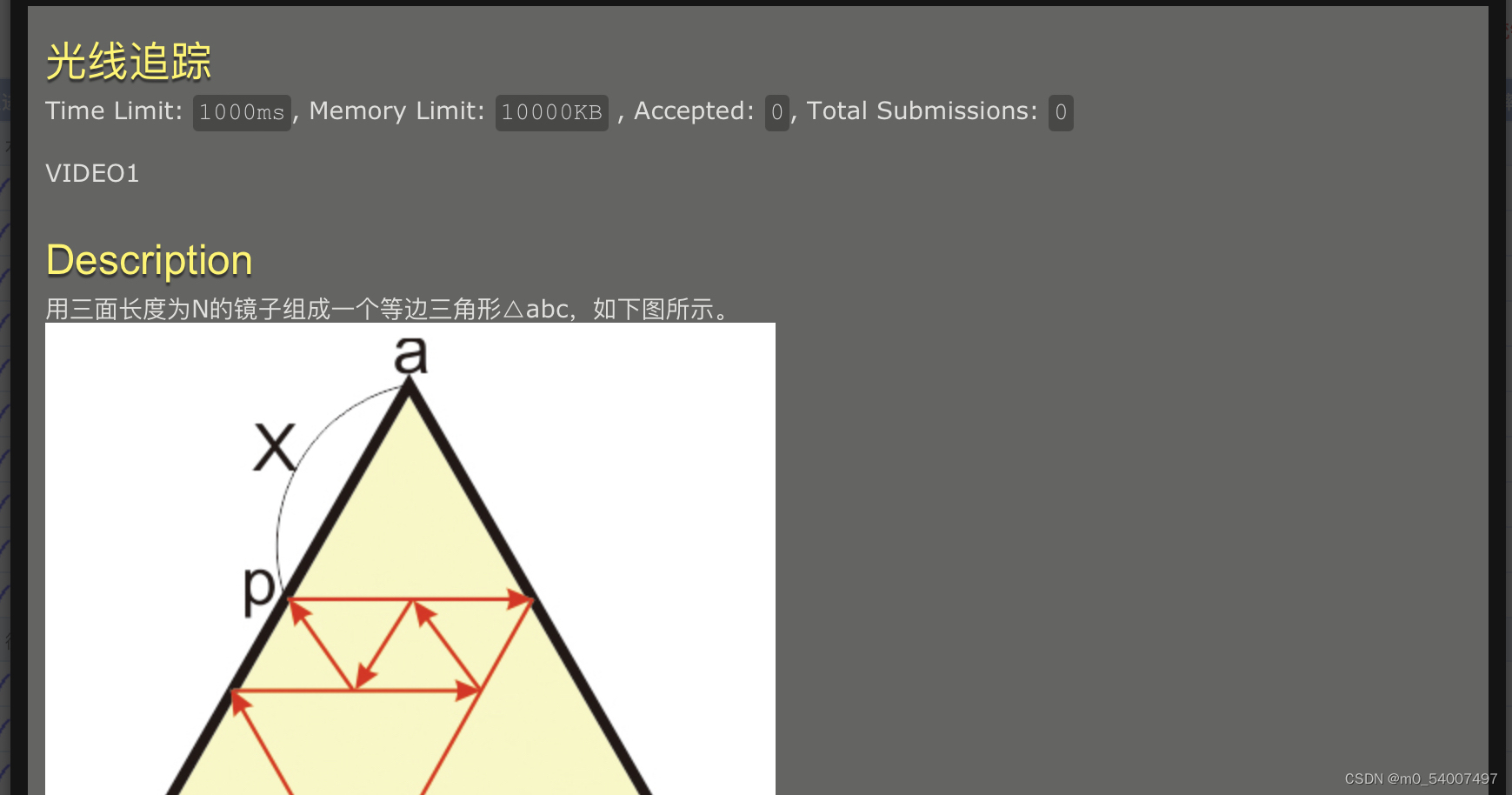
#include<stdio.h>long long solve(int a, int b) {if (a < b) {int t = a;a = b;b = t;}if (a % b == 0) {return a + a - b;}return a / b * (b + b) + solve(a % b, b);
}int main() {int n, x;scanf("%d%d", &n, &x);printf("%lld", solve(x, n - x) + n);
}

这个题感谢@Rrx050212同学的思路提供，如果看不懂的话可以试试这么画图

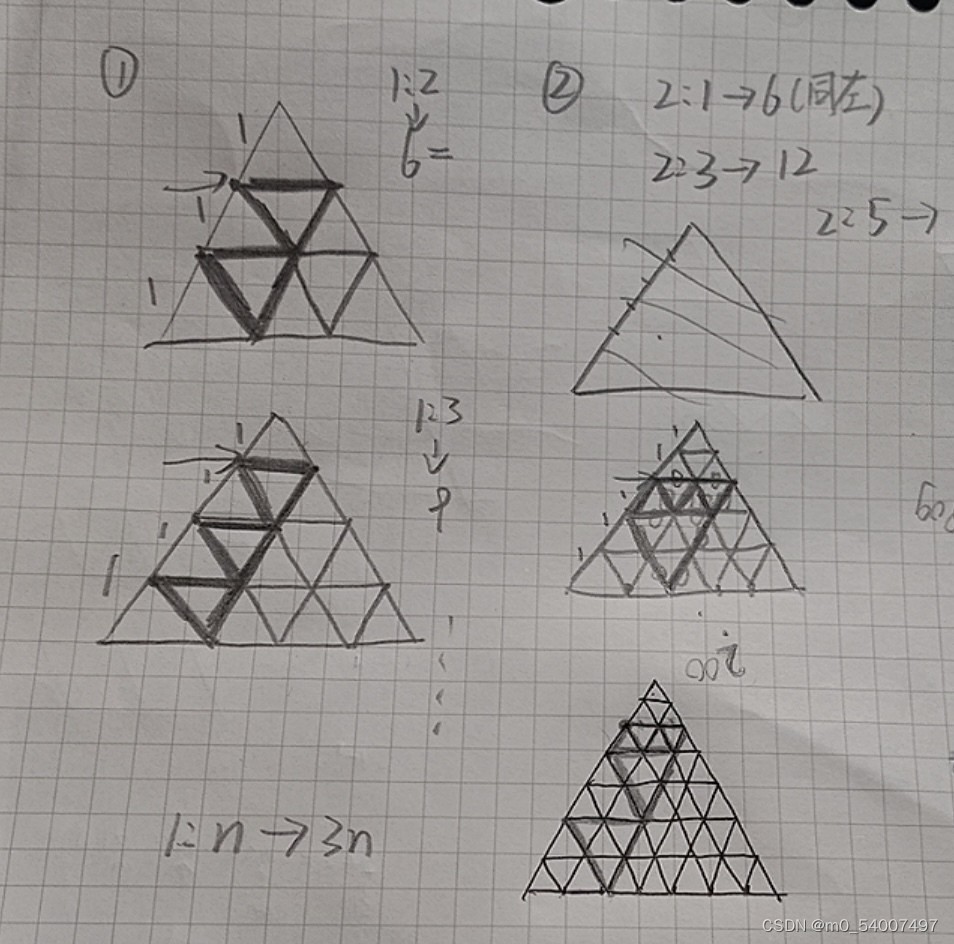
个人感觉这个题的推导过程很有意思，不妨自己推导一下

39.佩尔数

#include<stdio.h>
int main(){int a[1000];a[0]=0;a[1]=1;for(int i=2;i<1000;i++){a[i]=2*a[i-1]+a[i-2];}int b;scanf("%d",&b);printf("%d",a[b]);
}

本人比较懒狗，没有采用老师给的函数，直接写的佩尔数，我有罪

40.素数

#include <stdio.h>int is_prime(int num) {if (num < 2) {return 0;}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return 0;}}return 1;
}
int main(){int a,b;int count=0;scanf("%d%d",&a,&b);for(int i=a;i<b;i++){if(is_prime(i)==1){count++;}}printf("%d",count);
}

依旧是简单粗暴的方法，对每个数进行一次素数判断，如果符合就count++

41.完美矩阵

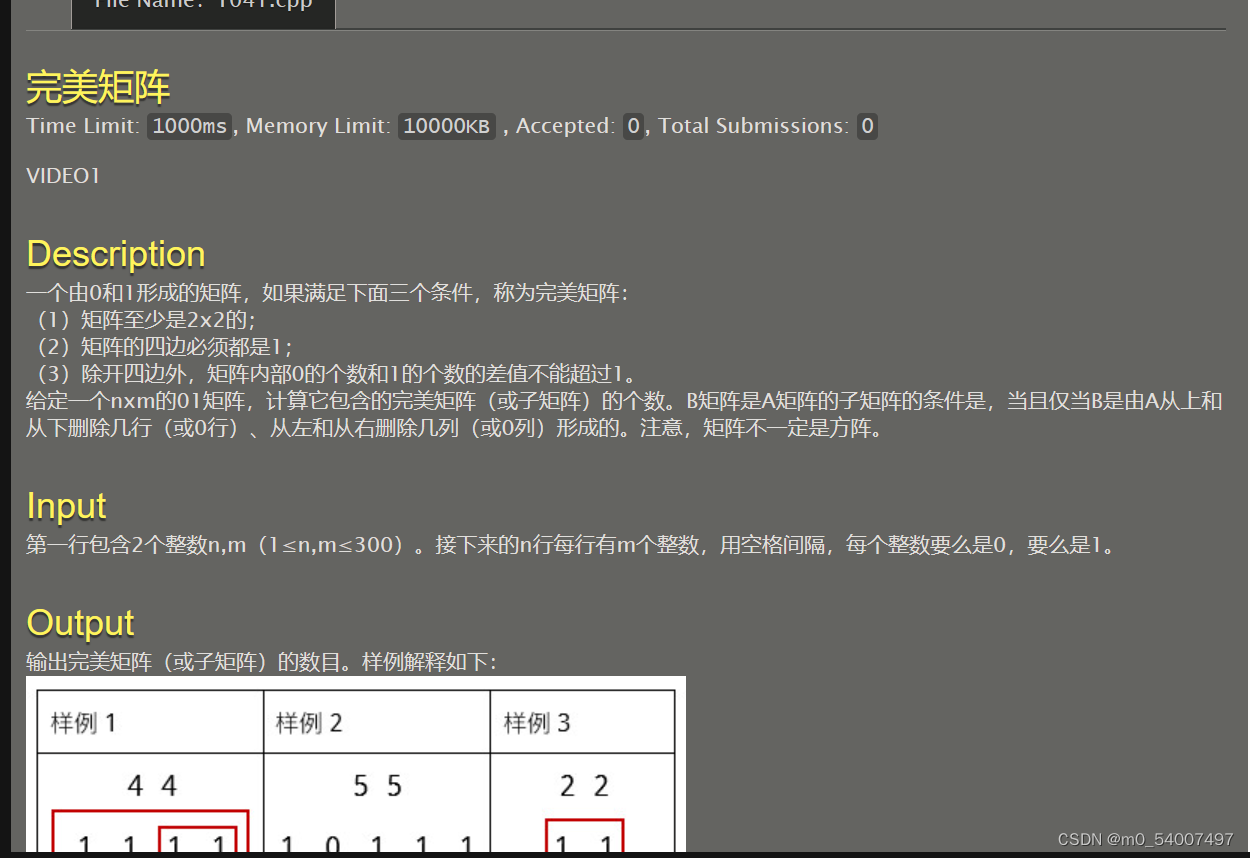
#include <stdio.h>
#include <stdlib.h>
#include <math.h>int isperfectarr(int** arr, int a, int b) {int count = 0;int num1 = 0;int num0 = 0;for (int i = 0; i < a; i++) {for (int j = 0; j < b; j++) {if (i == 0 || j == 0 || i == a - 1 || j == b - 1) {if (arr[i][j] == 1) {count++;}}}}if (count == a * b - (a - 2) * (b - 2)) {for (int i = 1; i < a - 1; i++) {for (int j = 1; j < b - 1; j++) {if (arr[i][j] == 1) {num1++;}else {num0++;}}}if (abs(num0 - num1) <= 1) {return 1;}}return 0;
}int main() {int** a;int length;int high;int count = 0;scanf("%d", &high);scanf("%d", &length);a = (int**)malloc(length * sizeof(int*));for (int i = 0; i < length; i++) {a[i] = (int*)malloc(high * sizeof(int));}for (int i = 0; i < length; i++) {for (int j = 0; j < high; j++) {scanf("%d", &a[i][j]);}}for (int i = 2; i <= length; i++) {for (int j = 2; j <= high; j++) {for (int m = 0; m <= length - i; m++) {for (int n = 0; n <= high - j; n++) {int** subarr = (int**)malloc(i * sizeof(int*));for (int k = 0; k < i; k++) {subarr[k] = (int*)malloc(j * sizeof(int));}for (int x = 0; x < i; x++) {for (int y = 0; y < j; y++) {subarr[x][y] = a[m + x][n + y];}}if (isperfectarr(subarr, i, j) == 1) {count++;}for (int k = 0; k < i; k++) {free(subarr[k]);}free(subarr);}}}}printf("%d\n", count);for (int i = 0; i < length; i++) {free(a[i]);}free(a);return 0;
}

最近比较忙，不想深究这个题，采用了@annesede的方法，这个题的说明有点问题，所有的完美矩阵都应该是方阵，基于这一点修改之前的代码应该是可以过的，但是懒得改了

https://blog.csdn.net/annesede/article/details/133761873?spm=1001.2014.3001.5501

#include <stdio.h>
#include <stdbool.h>#define MAXSIZE 301int arr[MAXSIZE][MAXSIZE] = {0};
int preSum[MAXSIZE][MAXSIZE] = {0};void prefix(int n, int m){for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1]- preSum[i - 1][j - 1] + arr[i][j];}}
}int getSum(int x1, int x2, int y1, int y2) {return preSum[x2][y2] - preSum[x1 - 1][y2] - preSum[x2][y1 - 1]+ preSum[x1 - 1][y1 - 1];
}bool isPerfect(int x1, int x2, int y1, int y2) {int outer = getSum(x1, x2, y1, y2), inner;int len = 2 * (x2 - x1 + y2 - y1);if ((x2 - x1) == 1 || (y2 - y1) == 1) inner = 0;else inner = getSum(x1 + 1, x2 - 1, y1 + 1, y2 - 1);if (inner != 1 && inner != 0 && inner != -1) return false;if ((outer - inner) != len) return false;return true;
}int perfectNum(int n, int m) {int cnt = 0;for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {for (int k = 1; k + i <= n && k + j <= m; ++k) {if (arr[i][k + j] == 0 || arr[k + i][j] == 0) break;if (isPerfect(i, i + k, j, j + k)) {++cnt;}}}}return cnt;
}int main () {int n, m;scanf("%d %d", &n, &m);for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {scanf("%d", &arr[i][j]);if (arr[i][j] == 0) arr[i][j] = -1;}}prefix(n ,m);printf("%d", perfectNum(n, m));return 0;
}

历所有可能的矩阵，但是wa，可能是超时导致的，需要换算法，但我懒得换了

42.货运优化

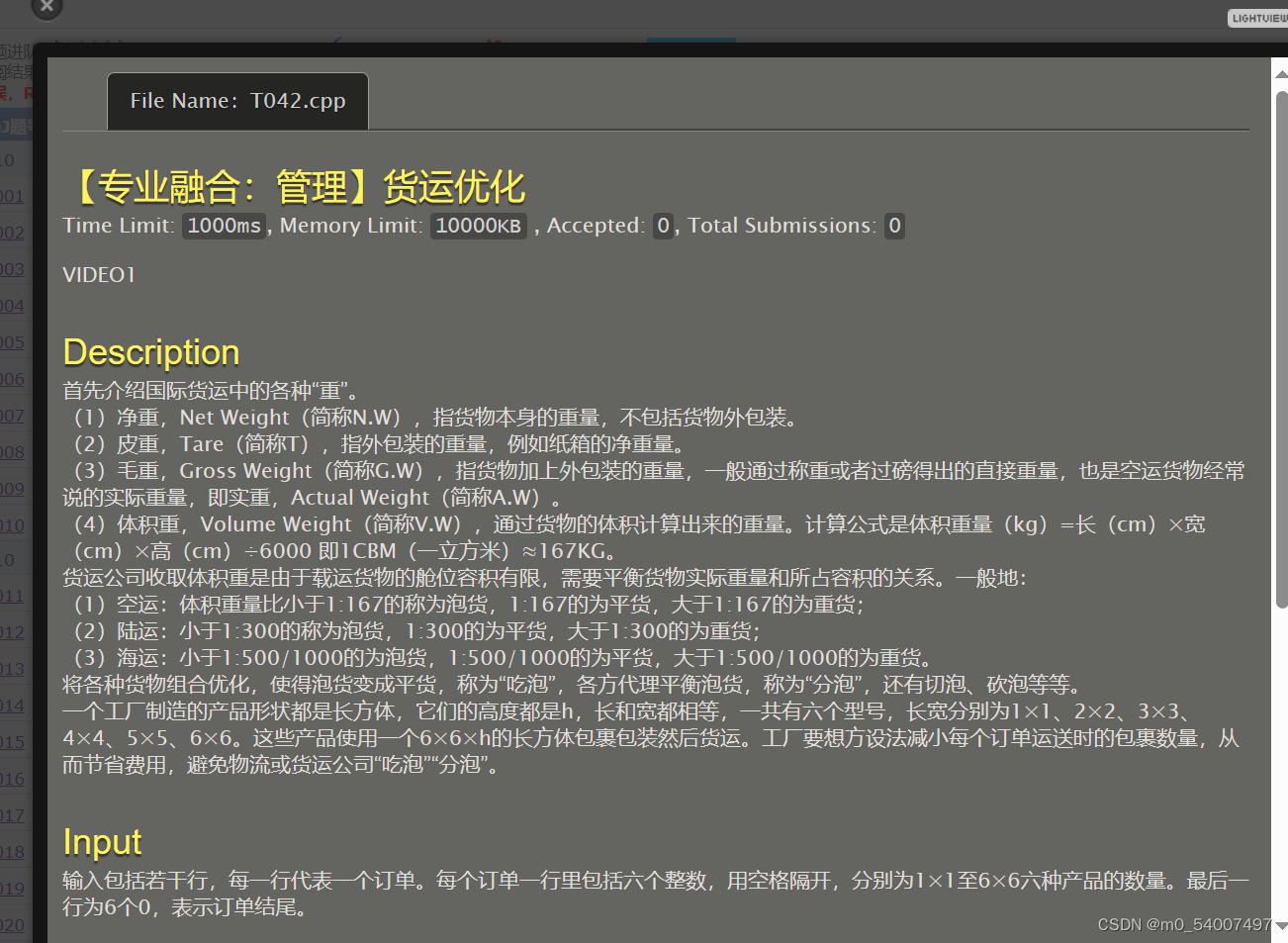
#include<stdio.h>
#include<math.h> // 导入math.h头文件
#define scanf_s scanf
int getcount(int* a) {int count = 0;int count1, count2, count3,count4=0,count5=0;count = a[5];//36占一个包裹count1 = a[4];//25占一个包裹count2 = a[3];//16占的包裹count3 = ceil(a[2]/4.0);//9占的包裹//讨论25和1组合后的1剩余数量int empty;//空余的empty = count1*36-a[4]*25;int residue;//剩余容量residue = empty - a[0];if (residue >= 0) {a[0] = 0;}else {a[0] = abs(residue);}//此时a[0]剩余a[0]个//讨论16和4组合后的余量int empty1;//空余的empty1 = count2 * 36 - a[3] * 16;int residue1;//剩余容量residue1 = empty1 - 4*a[1];if (residue >= 0) {a[1] = 0;}//如果还有剩余容量则a[1]装满else {a[1] = abs(residue)/4;// 剩余的a[1]数量}if (a[0] + a[1] != 0) {int empty2;//空余的empty2 = count3* 36 - a[2] * 9;int residue2;//剩余容量residue2 = empty2 - 4 * a[1];if (residue2 >= 0) {a[1] = 0;residue2 = residue2 - a[0];if (residue2 >= 0) {a[0] = 0;}else {a[0] = abs(residue2);count5 = ceil(a[0] / 36.0);a[0] = 0;//如果a[0]有多的就再分配一个包裹}}else {a[1] = abs(residue) / 4;}}//如果a[0]和a[1]有余量则放到9占的包裹的剩余之中if (a[0] + a[1] != 0) {count4 = ceil(a[1] / 9.0);// 为多余的4分配背包a[1] = 0;residue = count4 * 36 - 4 * a[1];if (residue >= 0) {a[0] = 0;}else {a[0] = abs(residue);count5 = ceil(a[0] / 36.0);a[0] = 0;}}if (a[0] + a[1] == 0) {/*printf("count=%d\n", count);printf("count1=%d\n", count1);printf("count2=%d\n", count2);printf("count3=%d\n", count3);printf("count4=%d\n", count4);printf("count5=%d\n", count5);*/return count + count1 + count2 + count3 + count4 + count5;}//已经全部分配完，可以返回了
}int main() {int a[6];int n;int count = 0;int b[1000] = { 0 };while (1) {for (int i = 0; i < 6; i++) {scanf_s("%d", &a[i]);}if (a[0] == 0 && a[1] == 0 && a[2] == 0 && a[3] == 0 && a[4] == 0 && a[5] == 0) {break;}b[count] = getcount(a);count++;}for (int i = 0; i < count; i++) {printf("%d\n", b[i]);}return 0;
}

用的贪心做的，注释写的很详细，根据注释来就行

43.波士顿房价预测

#include <stdio.h>void linear_regression(int n, double x[], double y[]) {double sum_x = 0, sum_y = 0, sum_xy = 0, sum_xx = 0;for (int i = 0; i < n; i++) {sum_x += x[i];sum_y += y[i];sum_xy += x[i] * y[i];sum_xx += x[i] * x[i];}double mean_x = sum_x / n;double mean_y = sum_y / n;double slope = (sum_xy - n * mean_x * mean_y) / (sum_xx - n * mean_x * mean_x);double intercept = mean_y - slope * mean_x;printf("Y=%.4f+%.4f*X\n", intercept, slope);
}int main() {int n;scanf("%d", &n);double x[n], y[n];for (int i = 0; i < n; i++) {scanf("%lf %lf", &x[i], &y[i]);}linear_regression(n, x, y);return 0;
}

题干太长直接没看，用的线性回归，如果有问题的话不如问问高中数学老师；

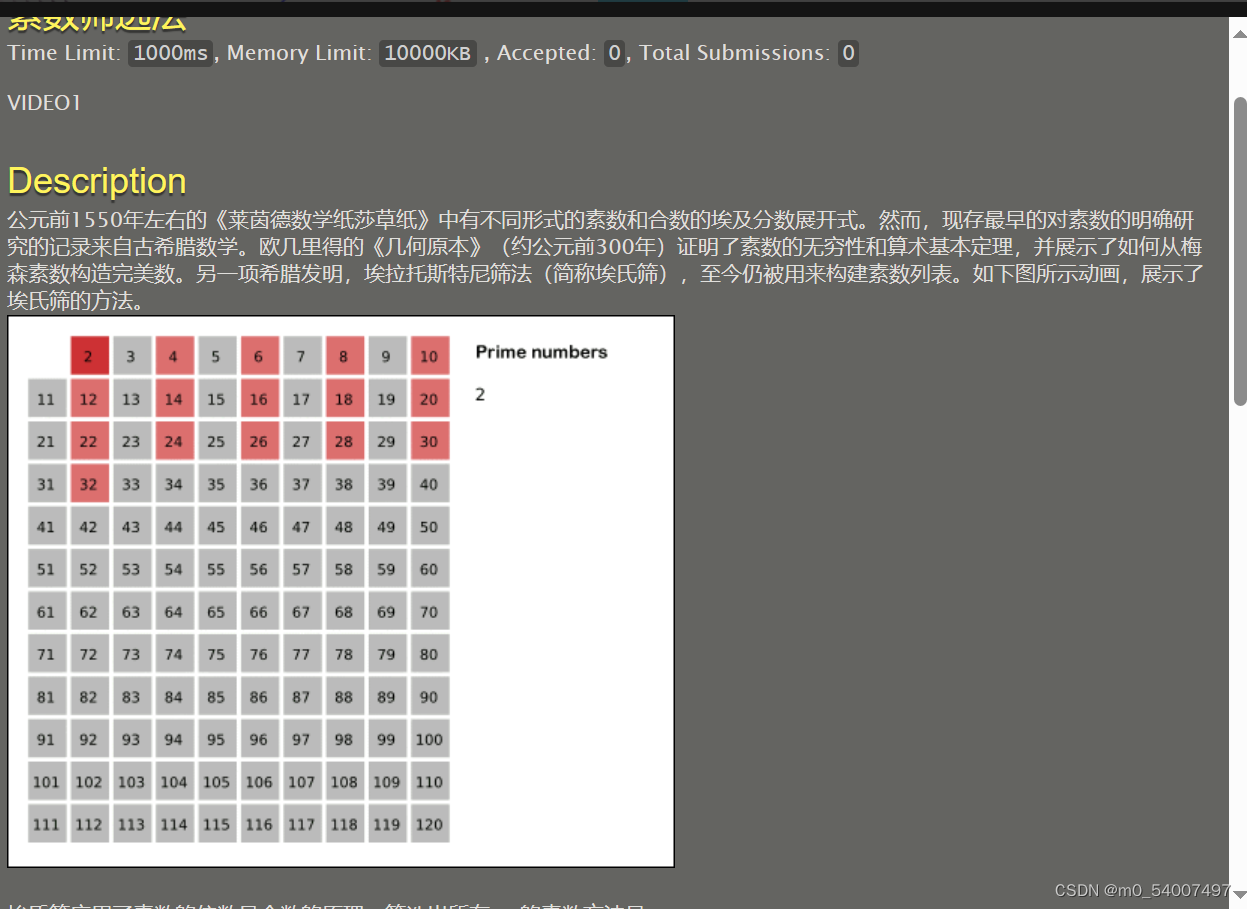
44.素数筛法

#include <stdio.h>
#include <stdbool.h>int countPrimes(int n) {if (n <= 2) {return 0;}bool isPrime[n];for (int i = 2; i < n; i++) {isPrime[i] = true;}for (int i = 2; i * i < n; i++) {if (isPrime[i]) {for (int j = i * i; j < n; j += i) {isPrime[j] = false;}}}int count = 0;for (int i = 2; i < n; i++) {if (isPrime[i]) {count++;}}return count;
}int main() {int n;scanf("%d", &n);int count = countPrimes(n);printf("%d",count);return 0;
}

筛素数，感觉不像是这个时候该出的题

45.稀疏矩阵

#include<stdio.h>
#include<stdlib.h>
int main(){int m;int n;int count=0;scanf("%d%d",&m,&n);int **arr;arr=(int **)malloc(m*sizeof(int *));for(int i=0;i<m;i++){arr[i]=(int *)malloc(n*sizeof(int));}for(int i=0;i<m;i++){for(int j=0;j<n;j++){scanf("%d",&arr[i][j]);if(arr[i][j]!=0){count++;}}}if(count<=m||count<=n||count<=0.05*(m*n)){printf("Yes");}else{printf("No");}
}

输入的时候检查一下是否非零然后和题干对比一下即可，很简单

46.回文数之和

#include<stdio.h>
bool isPalindrome(int num, int base) {int originalNum = num;int reversedNum = 0;while (num > 0) {reversedNum = reversedNum * base + num % base;num /= base;}return originalNum == reversedNum;
}
int main() {int a, b,sum=0;scanf("%d%d", &a, &b);for (int i = 0; i < a; i++) {if (isPalindrome(i,b)&& isPalindrome(i,10)) {sum=sum+i;}}printf("%d", sum);
}

判断一个数是否是回文数然后求和

47.航空旅行

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<algorithm>
#include<vector>
using namespace std;
bool cantake(int a, int b, int c, int d, int e) {int arr1[3] = { a,b,c };int arr2[2] = { d,e };sort(arr1, arr1 + 3);sort(arr2, arr2 + 2);if ((arr1[2] + arr1[1]) <= arr2[1] && arr1[0] <= arr2[0]) {return true;}else {return false;}
}
int main() {int n;scanf("%d", &n);vector<bool> arr(n);int a, b, c;int d, e;for (int i = 0; i < n; i++) {scanf("%d%d%d%d%d", &a, &b, &c, &d, &e);arr[i] = cantake(a, b, c, d, e);}for (int i = 0; i < n; i++) {if (arr[i]) {printf("YES\n");}else {printf("NO\n");}}
}

难得一见的简单题，把物品重量排个序然后看能不能托运和随身携带

48.蒙特卡罗方法求积分

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<algorithm>
#include<vector>//#define scanf scanf_s
using namespace std;double f(double x,int i) {if (i == 1) {return pow(x, 4) * exp(-x);}if (i == 2) {return pow(x, 2) + 1;}if (i == 3) {return cos(x);}if (i == 4)return pow(x, 1 / 2) * (x - 2);if (i == 5) {return 2 * sin(x) - 5 * cos(x);}
}double integral(int m,double a, double b, int n) {double sum = 0.0;double x, y;srand(RAND_MAX); for (int i = 0; i < n; i++) {x = a + (b - a) * rand() / RAND_MAX; y = f(x,m);sum += y;}return (b - a) * sum / n; 
}
int main() {double a, b;int n,m;scanf("%d", &m);scanf("%lf", &a);scanf("%lf", &b);scanf("%d", &n);double result = integral(m,a, b, n);printf("%.6lf.\n", result);return 0;
}

我不知道怎么改这个题，反正做不到样例输出，反而和别人有一样的错误答案

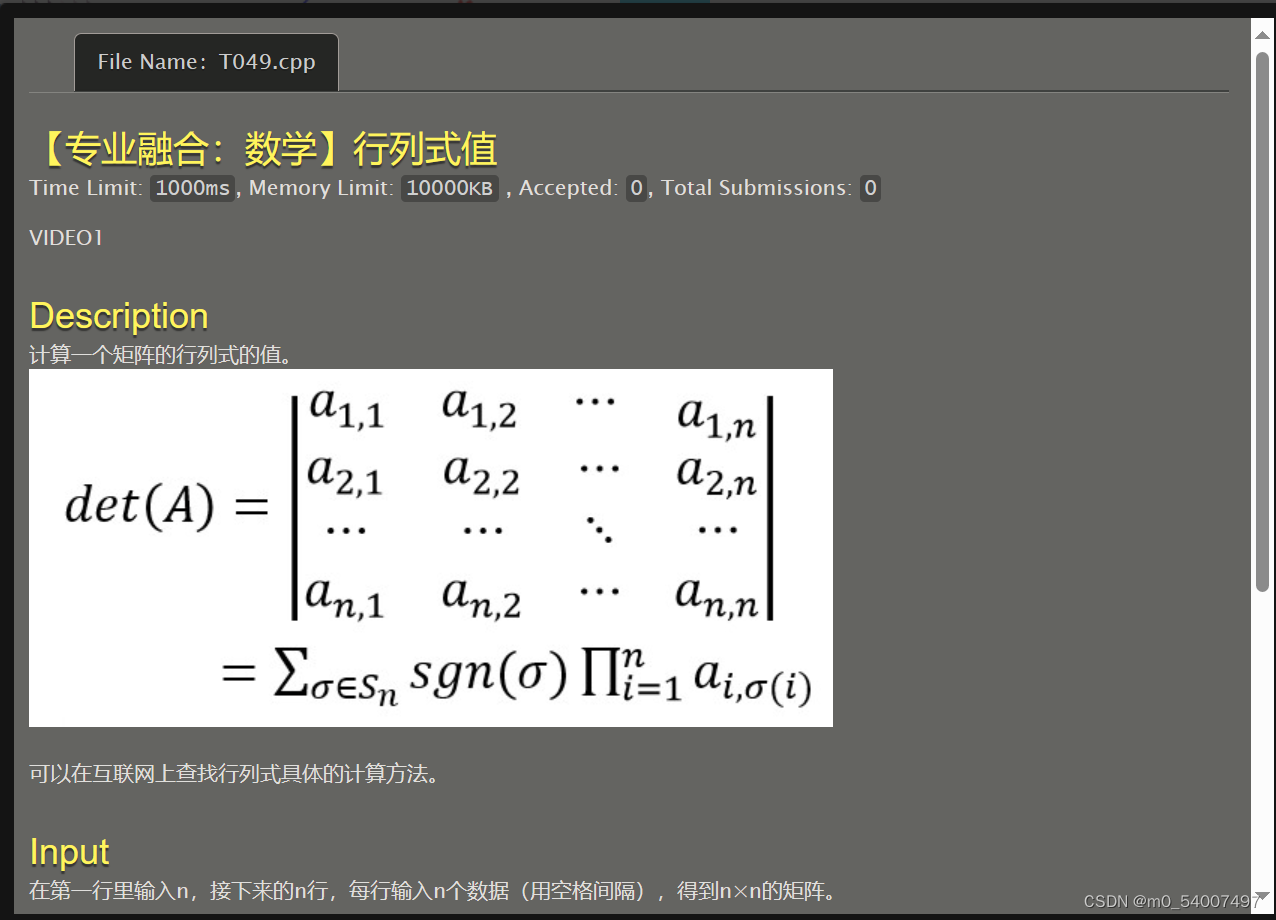
49.行列式

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
int** malloc2D(int n) {int** a;a = (int**)malloc(n * sizeof(int*));for (int i = 0; i < n; i++){a[i] = (int*)malloc(n * sizeof(int));}return a;
}
int Minor(int** arr1, int i, int n);
int DET(int** arr1, int n)
{int i, M, sum = 0;//i是第一行的列指标，M是余子式的值，sum是行列式的计算值if (n == 1)//一阶行列式直接得出结果return arr1[0][0];else if (n > 1){for (i = 0; i < n; i++)//按第一行展开{M = Minor(arr1, i, n);sum += pow(-1, i + 2) * arr1[0][i] * M;}}return sum;
}
int Minor(int** arr1, int i, int n)
{int  j, k, result;int** arr2=malloc2D(n);for (j = 0; j < n - 1; j++){for (k = 0; k < n - 1; k++){if (k < i)arr2[j][k] = arr1[j + 1][k];else if (k >= i)arr2[j][k] = arr1[j + 1][k + 1];}}return DET(arr2, n - 1);
}
int main() {int n;scanf("%d", &n);int** a = malloc2D(n);for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {scanf("%d", &a[i][j]);}}

按行按列展开行列式，递归，行列式的计算就不赘述了，自己查资料

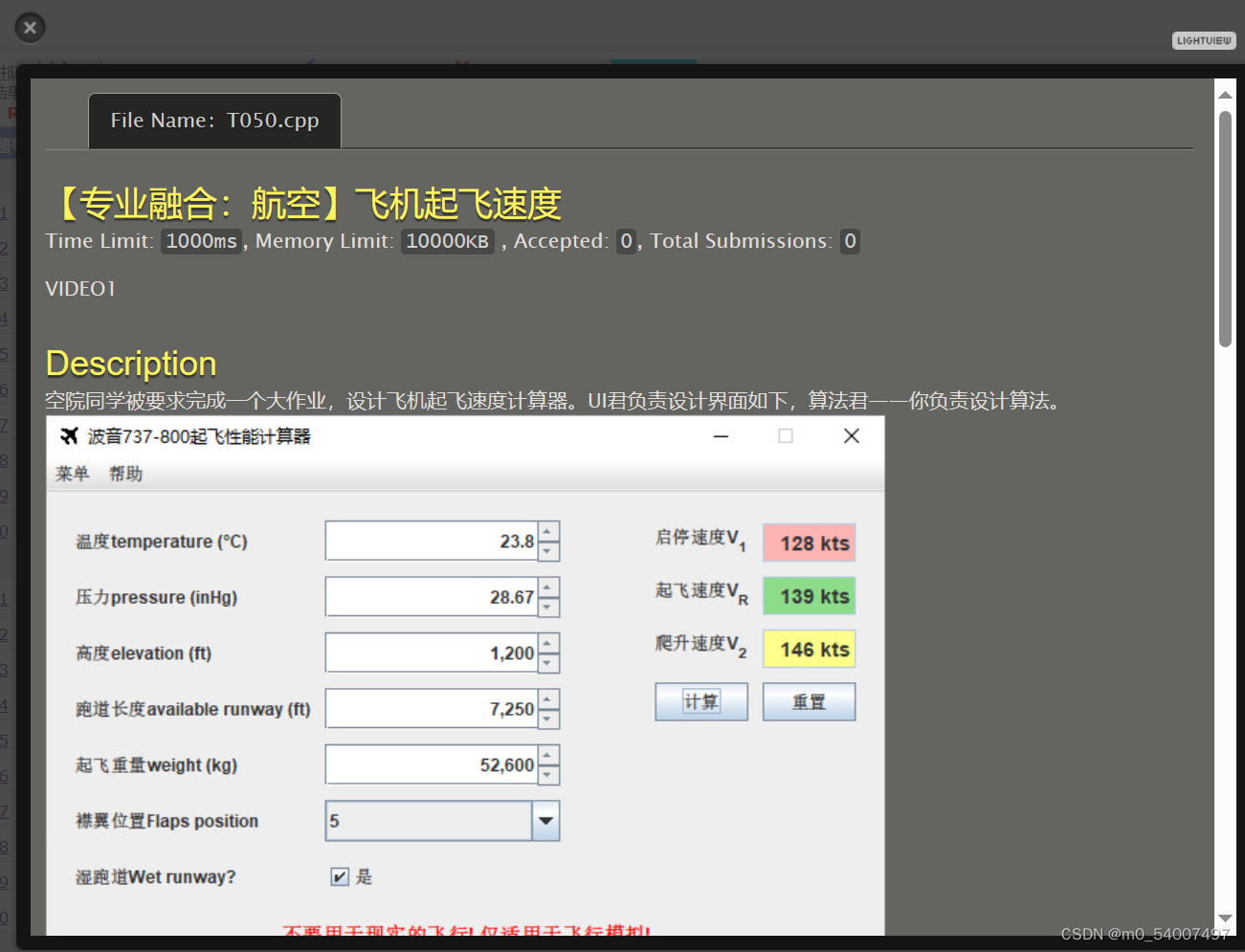
50.飞机起飞速度

#include <stdio.h>
#include <math.h>
#define scanf scanf_s
double calculateSpeed(double temperature, double pressure, int elevation, int runway, int weight, int flaps, int wet) {// 检查输入是否在有效范围内if (flaps != 1 && flaps != 5 && flaps != 15) {return -1;}if (weight < 41413 || weight > 65000 || runway <= 6900) {return -1;}// 计算温度档和气压档int tempRange = floor(temperature / 10);int pressureRange = ceil(pressure);// 检查操纵参考表是否存在if (tempRange < 0 || tempRange > 7 || pressureRange < 0 || pressureRange > 9) {return -1;}// 根据温度档和气压档查找操纵参考值char referenceTable[8][10] = {{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K'},{'L', 'M', 'N', 'P', 'Q', 'R', 'S', 'T', 'U', 'V'},{'W', 'X', 'Y', 'Z', 'A', 'B', 'C', 'D', 'E', 'F'},{'G', 'H', 'J', 'K', 'L', 'M', 'N', 'P', 'Q', 'R'},{'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'A', 'B'},{'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K', 'L', 'M'},{'N', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X'},{'Y', 'Z', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}};char reference = referenceTable[tempRange][pressureRange];// 检查操纵参考表是否存在V1、Vr和V2if (reference != 'A' && reference != 'B' && reference != 'C' && reference != 'D' && reference != 'E') {return -1;}// 根据襟翼位置、起飞重量和操纵参考值查找V1、Vr和V2int speedTable[3][5] = {{117, 126, 134, 142, 151},{122, 131, 139, 147, 156},{127, 136, 145, 153, 162}};int speedIndex = (flaps - 1) / 7;int* speedRow = speedTable[speedIndex];int v1 = speedRow[weight / 13000];int vr = speedRow[weight / 13000] + 11;int v2 = speedRow[weight / 13000] + 18;// 如果是湿跑道，根据跑道长度和襟翼位置查找折扣值if (wet == 1) {int discountTable[3][3] = {{0, 0, 0},{0, 0, 0},{0, 0, 0}};int discountIndex = (flaps - 1) / 7;int* discountRow = discountTable[discountIndex];int discount = discountRow[runway / 1000];v1 -= discount;}printf("V1=%dkts Vr=%dkts V2=%dkts\n", v1, vr, v2);return 0;
}int main() {double temperature, pressure;int elevation, runway, weight, flaps, wet;scanf("%lf %lf", &temperature, &pressure);scanf("%d %d %d %d %d", &elevation, &runway, &weight, &flaps, &wet);int result = calculateSpeed(temperature, pressure, elevation, runway, weight, flaps, wet);if (result == -1) {printf("Flight not possible!\n");}return 0;
}

最近感冒了，再加上事情比较多，41 48 50我暂时不会深究，这三道题是wa的，如果有能ac的大佬也请给我分享一下

之后的题暂时打开是乱码，暂且写到这，希望这个贴不要太监

这篇关于西北工业大学noj2023年c程序设计100题，更新中的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！