本文主要是介绍二维码的纠错码原理及如何纠错(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文将通过例子来说明两个方面的内容:
(1)如何构建纠错码?
(2)有了纠错码之后如何纠错?
1 如何构建纠错码?
直接上例子,“hello world” 利用二维码的编码原理,转换成十进制数字为“32, 91, 11, 120, 209, 114, 220, 77, 67, 64, 236, 17, 236, 17, 236, 17”,因此这个语句的消息多项式为:
32 x 15 + 91 x 14 + 11 x 13 + 120 x 12 + 209 x 11 + 114 x 10 + 220 x 9 + 77 x 8 + 67 x 7 + 64 x 6 + 236 x 5 + 17 x 4 + 236 x 3 + 17 x 2 + 236 x 1 + 17 (1) \begin{aligned} &32x^{15} + 91x^{14} + 11x^{13} + 120x^{12} + 209x^{11} + 114x^{10} + 220x^{9} + 77x^{8} + 67x^{7}\\ &+ 64x^{6} + 236x^{5} + 17x^{4} + 236x^{3} + 17x^{2} + 236x^{1} + 17 \end{aligned} \tag1 32x15+91x14+11x13+120x12+209x11+114x10+220x9+77x8+67x7+64x6+236x5+17x4+236x3+17x2+236x1+17(1)
1.1 生成多项式
从下面这个网址可以轻松得到 n ≥ 7 n≥7 n≥7的生成多项式:
https://www.thonky.com/qr-code-tutorial/generator-polynomial-tool?degree=7
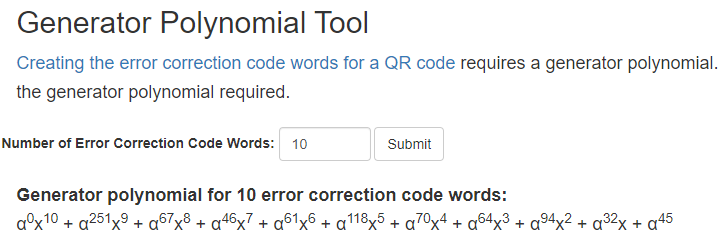
1.2 多项式除法
“Hello world”完整的消息多项式见公式(1),为了确保在除法期间引导项的指数不会变得太小,将消息多项式乘以 x n x^n xn, n n n是所需的纠错码字的数量。如当纠错码字的数量是10时,式(1)应该变成:
32 x 25 + 91 x 24 + 11 x 23 + 120 x 22 + 209 x 21 + 114 x 20 + 220 x 19 + 77 x 18 + 67 x 17 + 64 x 16 + 236 x 15 + 17 x 14 + 236 x 13 + 17 x 12 + 236 x 11 + 17 x 10 (2) \begin{aligned} &32x^{25} + 91x^{24} + 11x^{23} + 120x^{22} + 209x^{21} + 114x^{20} + 220x^{19} + 77x^{18} + 67x^{17} \\ &+ 64x^{16} + 236x^{15} + 17x^{14} + 236x^{13} + 17x^{12} + 236x^{11} + 17x^{10} \end{aligned} \tag2 32x25+91x24+11x23+120x22+209x21+114x20+220x19+77x18+67x17+64x16+236x15+17x14+236x13+17x12+236x11+17x10(2)
生成多项式的前导项也应该具有相同的指数,因此生成多项式也乘 x 15 x^{15} x15得到下式:
α 0 x 25 + α 251 x 24 + α 67 x 23 + α 46 x 22 + α 61 x 21 + α 118 x 20 + α 70 x 19 + α 64 x 18 + α 94 x 17 + α 32 x 16 + α 45 x 15 (3) \begin{aligned} &α^0x^{25} + α^{251}x^{24} + α^{67}x^{23} + α^{46}x^{22} + α^{61}x^{21} + α^{118}x^{20} + \\ &α^{70}x^{19} + α^{64}x^{18} + α^{94}x^{17} + α^{32}x^{16} + α^{45}x^{15} \end{aligned} \tag3 α0x25+α251x24+α67x23+α46x22+α61x21+α118x20+α70x19+α64x18+α94x17+α32x16+α45x15(3)
具体除法步骤如下:
(1)将生成多项式乘以消息多项式的前导项。
消息多项式的前导项是32,也就是 α 5 α^5 α5,乘上生成多项式后,生成多项式变成:
α 5 x 25 + α 256 % 255 x 24 + α 72 x 23 + α 51 x 22 + α 66 x 21 + α 123 x 20 + α 75 x 19 + α 69 x 18 + α 99 x 17 + α 37 x 16 + α 50 x 15 = α 5 x 25 + α 1 x 24 + α 72 x 23 + α 51 x 22 + α 66 x 21 + α 123 x 20 + α 75 x 19 + α 69 x 18 + α 99 x 17 + α 37 x 16 + α 50 x 15 = 32 x 25 + 2 x 24 + 101 x 23 + 10 x 22 + 97 x 21 + 197 x 20 + 15 x 19 + 47 x 18 + 134 x 17 + 74 x 16 + 5 x 15 (4) \begin{aligned} &α^5x^{25} + α^{256 \% 255}x^{24} + α^{72}x^{23} + α^{51}x^{22} + α^{66}x^{21} + α^{123}x^{20} + \\ &α^{75}x^{19} + α^{69}x^{18} + α^{99}x^{17} + α^{37}x^{16} + α^{50}x^{15} \\ &= α^5x^{25} + α^{1}x^{24} + α^{72}x^{23} + α^{51}x^{22} + α^{66}x^{21} + α^{123}x^{20} + \\ &α^{75}x^{19} + α^{69}x^{18} + α^{99}x^{17} + α^{37}x^{16} + α^{50}x^{15} \\ &= 32x^{25} + 2x^{24} + 101x^{23} + 10x^{22} + 97x^{21} + 197x^{20} + \\ &15x^{19} + 47x^{18} + 134x^{17} + 74x^{16} + 5x^{15} \end{aligned} \tag4 α5x25+α256%255x24+α72x23+α51x22+α66x21+α123x20+α75x19+α69x18+α99x17+α37x16+α50x15=α5x25+α1x24+α72x23+α51x22+α66x21+α123x20+α75x19+α69x18+α99x17+α37x16+α50x15=32x25+2x24+101x23+10x22+97x21+197x20+15x19+47x18+134x17+74x16+5x15(4)
(2) 使用消息多项式对结果进行异或。
从下面这个式子也可以看出来,就是消息多项式和生成多项式中相同次数的项的系数进行了异或操作,经过这个操作之后,消息多项式中最高次数的项已经没有了(因为生成多项式和消息多项式拥有完全相同的第一项,一异或就没了)。
( 32 ⊕ 32 ) x 25 + ( 91 ⊕ 2 ) x 24 + ( 11 ⊕ 101 ) x 23 + ( 120 ⊕ 10 ) x 22 + ( 209 ⊕ 97 ) x 21 + ( 114 ⊕ 197 ) x 20 + ( 220 ⊕ 15 ) x 19 + ( 77 ⊕ 47 ) x 18 + ( 67 ⊕ 134 ) x 17 + ( 64 ⊕ 74 ) x 16 + ( 236 ⊕ 5 ) x 15 + ( 17 ⊕ 0 ) x 14 + ( 236 ⊕ 0 ) x 13 + ( 17 ⊕ 0 ) x 12 + ( 236 ⊕ 0 ) x 11 + ( 17 ⊕ 0 ) x 10 = 0 x 25 + 89 x 24 + 110 x 23 + 114 x 22 + 176 x 21 + 183 x 20 + 211 x 19 + 98 x 18 + 197 x 17 + 10 x 16 + 233 x 15 + 17 x 14 + 236 x 13 + 17 x 12 + 236 x 11 + 17 x 10 = 89 x 24 + 110 x 23 + 114 x 22 + 176 x 21 + 183 x 20 + 211 x 19 + 98 x 18 + 197 x 17 + 10 x 16 + 233 x 15 + 17 x 14 + 236 x 13 + 17 x 12 + 236 x 11 + 17 x 10 (5) \begin{aligned} &(32 \oplus 32)x^{25} + (91 \oplus 2)x^{24} + (11 \oplus 101)x^{23} + (120 \oplus 10)x^{22} + (209 \oplus 97)x^{21} \\ &+ (114 \oplus 197)x^{20} + (220 \oplus 15)x^{19} + (77 \oplus 47)x^{18} + (67 \oplus 134)x^{17} + (64 \oplus 74)x^{16} \\ &+ (236 \oplus 5)x^{15} + (17 \oplus 0) x^{14} + (236 \oplus 0)x^{13} + (17 \oplus 0)x^{12} + (236 \oplus 0)x^{11} + (17 \oplus 0)x^{10} \\ &= 0x^{25} + 89x^{24} + 110x^{23} + 114x^{22} + 176x^{21} + 183x^{20} + 211x^{19} + 98x^{18} + 197x^{17} \\ &+ 10x^{16} + 233x^{15} + 17x^{14} + 236x^{13} + 17x^{12} + 236x^{11} + 17x^{10} \\ &= 89x^{24} + 110x^{23} + 114x^{22} + 176x^{21} + 183x^{20} + 211x^{19} + 98x^{18} + 197x^{17} \\ &+ 10x^{16} + 233x^{15} + 17x^{14} + 236x^{13} + 17x^{12} + 236x^{11} + 17x^{10} \end{aligned} \tag5 (32⊕32)x25+(91⊕2)x24+(11⊕101)x23+(120⊕10)x22+(209⊕97)x21+(114⊕197)x20+(220⊕15)x19+(77⊕47)x18+(67⊕134)x17+(64⊕74)x16+(236⊕5)x15+(17⊕0)x14+(236⊕0)x13+(17⊕0)x12+(236⊕0)x11+(17⊕0)x10=0x25+89x24+110x23+114x22+176x21+183x20+211x19+98x18+197x17+10x16+233x15+17x14+236x13+17x12+236x11+17x10=89x24+110x23+114x22+176x21+183x20+211x19+98x18+197x17+10x16+233x15+17x14+236x13+17x12+236x11+17x10(5)
(3) 将生成多项式乘上一步的XOR结果的前导项。注意,这里的生成多项式已经经过了和现在的信息多项式等指数的过程,所以最高次是24。
在这个例子中,前导项是 89 x 24 89x^{24} 89x24,做乘法的时候,把数字用α表示比较简单,89又等于 α 210 α^{210} α210(这个可以查表得),所以:
( α 210 ∗ α 0 ) x 24 + ( α 210 ∗ α 251 ) x 23 + ( α 210 ∗ α 67 ) x 22 + ( α 210 ∗ α 46 ) x 21 + ( α 210 ∗ α 61 ) x 20 + ( α 210 ∗ α 118 ) x 19 + ( α 210 ∗ α 70 ) x 18 + ( α 210 ∗ α 64 ) x 17 + ( α 210 ∗ α 94 ) x 16 + ( α 210 ∗ α 32 ) x 15 + ( α 210 ∗ α 45 ) x 14 = α 210 x 24 + α 206 x 23 + α 22 x 22 + α 1 x 21 + α 16 x 20 + α 73 x 19 + α 25 x 18 + α 19 x 17 + α 49 x 16 + α 242 x 15 + α 0 x 14 = 89 x 24 + 83 x 23 + 234 x 22 + 2 x 21 + 76 x 20 + 202 x 19 + 3 x 18 + 90 x 17 + 140 x 16 + 176 x 15 + 1 x 14 (6) \begin{aligned} & (α^{210} * α^{0})x^{24} + (α^{210} * α^{251})x^{23} + (α^{210} * α^{67})x^{22} + (α^{210} * α^{46})x^{21} \\ &+ (α^{210} * α^{61})x^{20} + (α^{210} * α^{118})x^{19} + (α^{210} * α^{70})x^{18} + (α^{210} * α^{64})x^{17} \\ &+ (α^{210} * α^{94})x^{16} + (α^{210} * α^{32})x^{15} + (α^{210} * α^{45})x^{14} \\ &= α^{210}x^{24} + α^{206}x^{23} + α^{22}x^{22} + α^{1}x^{21} + α^{16}x^{20} \\ &+ α^{73}x^{19} + α^{25}x^{18} + α^{19}x^{17} + α^{49}x^{16} + α^{242}x^{15} + α^{0}x^{14} \\ &= 89x^{24} + 83x^{23} + 234x^{22} + 2x^{21} + 76x^{20} + 202x^{19} + 3x^{18} + 90x^{17} \\ &+ 140x^{16} + 176x^{15} + 1x^{14} \end{aligned} \tag6 (α210∗α0)x24+(α210∗α251)x23+(α210∗α67)x22+(α210∗α46)x21+(α210∗α61)x20+(α210∗α118)x19+(α210∗α70)x18+(α210∗α64)x17+(α210∗α94)x16+(α210∗α32)x15+(α210∗α45)x14=α210x24+α206x23+α22x22+α1x21+α16x20+α73x19+α25x18+α19x17+α49x16+α242x15+α0x14=89x24+83x23+234x22+2x21+76x20+202x19+3x18+90x17+140x16+176x15+1x14(6)
(4) 将上一步得到的式子继续重复类似步骤2的异或操作,这个操作之后,最前面那项(次数为24次的那项)又成功没有了。
那么重复到什么时候好呢?从上面可以看出来,循环一次,就有一个消息多项式中的一项被消除,所以消息多项式有多少项,就进行多少次循环(这就好像除法进行到了最后一位)。上述例子循环16次后,就得到了下面这个式子(从这个式子中我们就可以看出来,刚开始的时候乘x^10有多明智,为什么是10而不是9或者8也从这里可以看出,因为生成多项式的最高次数是纠错码字的数目,一项项异或之后,最后的余数的位数和生成多项式的位数是相关的)
196 x 9 + 35 x 8 + 39 x 7 + 119 x 6 + 235 x 5 + 215 x 4 + 231 x 3 + 226 x 2 + 93 x 1 + 23 (7) \begin{aligned} &196x^{9} + 35x^{8} + 39x^{7} \\ &+ 119x^{6} + 235x^{5} + 215x^{4} + 231x^{3} + 226x^{2} + 93x^{1} + 23 \end{aligned} \tag7 196x9+35x8+39x7+119x6+235x5+215x4+231x3+226x2+93x1+23(7)
现在我们就得到纠错码字了:196 35 39 119 235 215 231 226 93 23
得到纠错码字之后就是按照规范给填到二维码的格子里面。
2 如何进行纠错?
二维码采用Reed-Solomon Codes(简称RS编码)进行纠错。
2.1 RS编码
RS编码以word为编码和解码单位,大的数据块拆分到字长为 w w w(取值一般为8或者16位)的word,然后对word进行编解码。 数据块的编码原理与word编码原理相同,后文中以word为例说明,变量 D i \mathrm{D_i} Di, C j \mathrm{C_j} Cj将分别代表第 i i i个数据码和第 j j j个纠错码(以word为单位)。
输入数据为向量 D = ( D 1 , D 2 , … , D n ) \mathrm{D} =(\mathrm{D_1},\mathrm{D_2},\dots, \mathrm{D_n}) D=(D1,D2,…,Dn),编码后为向量 ( D 1 , D 2 , … , D n , C 1 , C 2 , … , C m ) (\mathrm{D_1},\mathrm{D_2},\dots, \mathrm{D_n}, \mathrm{C_1}, \mathrm{C_2}, \dots, \mathrm{C_m}) (D1,D2,…,Dn,C1,C2,…,Cm),RS编码可表示为如下图所示矩阵运算:

上图最左边是编码矩阵(或称为生成矩阵、分布矩阵,Distribution Matrix),编码矩阵需要满足任意 n × n n \times n n×n子矩阵可逆。
为方便数据存储,编码矩阵上部是单位阵( n n n行 n n n列),下部是 m m m行 n n n列矩阵。下部矩阵可以选择范德蒙德矩阵或柯西矩阵。后文说明。
2.2 RS编码数据恢复原理
RS最多能容忍 k k k个数据块被删除。 数据恢复的过程如下:
(1)假设 D 1 \mathrm{D_1} D1、 D 4 \mathrm{D_4} D4、 C 2 \mathrm{C_2} C2丢失,从编码矩阵中删掉丢失的数据块/编码块对应的行。
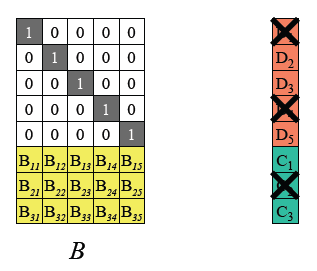
(2)根据图1所示RS编码运算等式,可以得到如下 B ′ \mathrm{B'} B′以及等式。
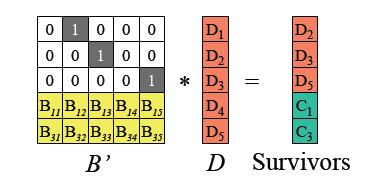
(3)由于 B ′ \mathrm{B'} B′是可逆的,记 B ′ \mathrm{B'} B′的逆矩阵为 B ′ − 1 \mathrm{B'}^{-1} B′−1,则 B ′ × B ′ − 1 = I \mathrm{B'} \times \mathrm{B'}^{-1} = \mathrm{I} B′×B′−1=I 单位矩阵。两边左乘 B ′ \mathrm{B'} B′逆矩阵 B ′ − 1 \mathrm{B'}^{-1} B′−1后如下图:
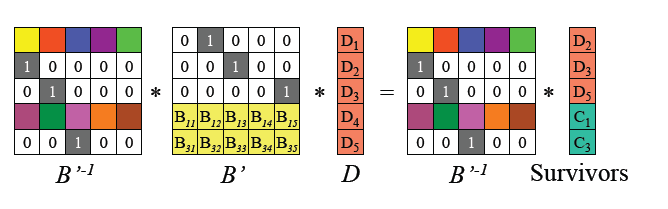
(4)得到如下原始数据 D \mathrm{D} D的计算公式:
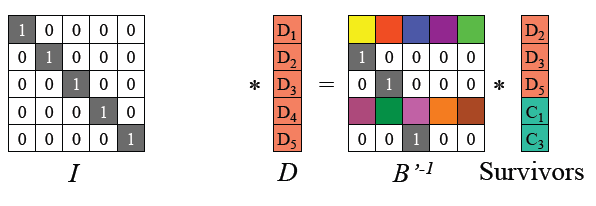
恢复原始数据 D \mathrm{D} D:
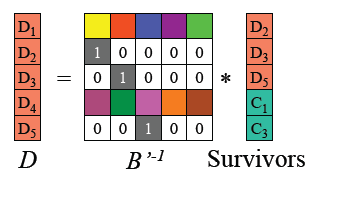
(5)对 D \mathrm{D} D重新编码,可得到丢失的编码。
3 下一步工作
下一步将讨论范德蒙德(Vandermonde)矩阵和柯西( Cauchy)矩阵。
这篇关于二维码的纠错码原理及如何纠错(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




