Wandering Robot ( ZOJ 4115 ) (第十届ACM山东省省赛 - C题 )

欢迎访问https://blog.csdn.net/lxt_Lucia～～

宇宙第一小仙女\(^o^)/～萌量爆表求带飞=≡Σ((( つ^o^)つ~ dalao们点个关注呗～

--------------------------------我只是一条可爱哒分界线-------------------------------

一、问题：

Description

DreamGrid creates a programmable robot to explore an infinite two-dimension plane. The robot has a basic instruction sequence a1,a2,...,an and a "repeating parameter" k, which together form the full instruction sequence s1,s2,...sn,sn+1,...snk, and control the robot.

There are 4 types of valid instructions in total, which are 'U' (up), 'D' (down), 'L' (left) and 'R' (right). Assuming that the robot is currently at , the instructions control the robot in the way below:

• U: Moves the robot to ( x, y+1 ) .
• D: Moves the robot to ( x, y-1 ).
• L: Moves the robot to  ( x-1, y ).
• R: Moves the robot to ( x+1, y ).

The full instruction sequence can be derived from the following equations:

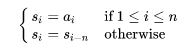
The robot is initially at (0,0) and executes the instructions in the full instruction sequence one by one. To estimate the exploration procedure, DreamGrid would like to calculate the largest Manhattan distance between the robot and the start point (0,0) during the execution of the nk instructions.

Recall that the Manhattan distance between (x1, y1) and (x2, y2) is defined as | x1-x2 | + | y1-y2 |.

Input

There are multiple test cases. The first line of the input contains an integer T indicating the number of test cases. For each test case:

The first line contains two integers  , indicating the length of the basic instruction sequence and the repeating parameter.

The second line contains a string  where a [ i ] indicates the i-th instruction in the basic instruction sequence.

It's guaranteed that the sum of |A| of all test cases will not exceed .

Output

For each test case output one line containing one integer indicating the answer.

Sample Input

2

3 3

RUL

1 1000000000

D

Sample Output

4

1000000000

Hint

For the first sample test case, the final instruction sequence is "RULRULRUL" and the route of the robot is (0, 0) - (1, 0) - (1, 1) - (0, 1) - (1, 1) - (1, 2) - (0, 2) - (1, 2) - (1, 3) - (0, 3). It's obvious that the farthest point on the route is (1, 3) and the answer is 4.

二、题意：

有一个机器人，会根据输入的命令走路，U代表向上，D代表向下，L代表向左，R代表向右，求：按给出的命令执行 k 遍的过程中，到达原点最远的距离是多少。两点距离：(x1, y1) 和 (x2, y2)按 | x1-x2 | + | y1-y2 | 计算。

三、思路：

当时做这个题的时候思路偏了，当时想的是，求出先求出第一遍的过程中经过的最远距离，再求第二遍和第三遍的差值，即每次移动当前这一次对上一次的影响，以后也都会按照这个影响进行移动，直到 k 次结束。

当时试了几十组也没找到bug，但其实这个思路的确是错的，举个栗子( 测试样例 )：

1

13 10

URDDDDLLUUUUR

答案应该是11 。

假设第一轮执行得到的最大值是在第三象限(左下角)，然后每次的终点都在起点上面1个单位，那么在 k 还不足以让整个过程轨迹都在 x 轴上方时，这么做是正确的，但是如果 k 足够大，使得后来的过程轨迹在 x 轴上方很远，其距离超过了第一轮(左下角)的，那么最大值应该在顶部，而不再是左下角的位置了。

正确的思路：

其实只需要考虑第一次和最后一次得到的最大值就可以了，最大值只可能在这两个时候出现。

首先，单算第一次，执行一遍，得到一个最大值，执行结束后得到第一遍的终点 ( x , y ) 。

然后，将 x 和 y 分别乘 ( k-1 ) 得到了第 k-1 次的终点坐标，即第 k 次的起点坐标。

然后，再执行一遍 ( 即第 k 遍 ) ，然后比较第一次和最后一次的最大值，即为结果。

注意：要开 long long！

四、代码：

#include <cstdio>
#include <algorithm>using namespace std;
typedef long long ll;int main()
{int T, n, k;char a[100010];while( ~scanf("%d", &T) ){while(T--){scanf("%d %d", &n, &k);scanf(" %s", a);ll x = 0, y = 0, max1 = 0;for(int i = 0; i <= n-1; i++)  //求第一遍最大值{if(a[i] == 'U')y++;else if(a[i] == 'D')y--;else if(a[i] == 'L')x--;else if(a[i] == 'R')x++;max1 = max(max1, abs(x)+abs(y));}x *= (k-1), y *= (k-1);for(int i = 0; i <= n-1; i++)   //求第k遍最大值{if(a[i] == 'U')y++;else if(a[i] == 'D')y--;else if(a[i] == 'L')x--;else if(a[i] == 'R')x++;max1 = max(max1, abs(x)+abs(y));}printf("%lld\n", max1);}}return 0;
}

--------------------------------我也是有底线的---------------------------------

宇宙第一小仙女\(^o^)/～萌量爆表求带飞=≡Σ((( つ^o^)つ~ dalao们点个关注呗～