Tria树(前缀树)与AC自动机

Tria树(前缀树)

介绍

前缀树是一种用于插入查找搜索数据的数据结构，又叫做字典树。后缀树与其类似。和哈希表相比，前缀树不仅可以查找某一个键，也可以查找该键的前缀。并且查找速度只与所要查找的键的字符长度有关。

数据结构

一个只存储小写字母的tria树的数据结构如下:

struct Trienode{bool is_string = false; //是否是结尾Trienode* next[26] = {NULL};
}*root;

插入，搜索，查找

• 初始化

root = new Trienode();	//初始化

• 插入

void insert(string word) {Trienode *p = root;for(int i=0;i<word.size();i++){if(p->next[word[i]-'a']==NULL)p->next[word[i]-'a'] = new Trienode();p = p->next[word[i]-'a'];}p->is_string = true;return;
}

• 查找字符串是否存在

bool search(string word) {Trienode *p = root;for(int i=0;i<word.size();i++){if(p->next[word[i]-'a']==NULL)return false;p = p->next[word[i]-'a'];}return p->is_string;
}

• 查找前缀是否存在

bool startsWith(string prefix) {Trienode*p =root;for(int i=0;i<prefix.size();i++){if(p->next[prefix[i]-'a']==NULL)return false;p = p->next[prefix[i]-'a'];}return true;
}

AC自动机

介绍

AC自动机,结合了KMP和Tria树。给tria树中的每个结点增加了一个fail指针,当匹配失败时跳转。(找到当前已经有的前缀相等的最长后缀！) 。

• 构造fail指针的思路如下:

通过bfs(队列)构造fail指针,根结点无fail指针(或者指向空).第一层fail指针指向根节点。当一个结点A遇到字母’a’失配时,他的父亲结点B通过’b’匹配带该结点,找到他父亲的fail指针指向的结点,如果他的父亲的fai指针指向的结点能够匹配’b’到结点C,则结点A的fail结点指向结点C。（B不符合则循环向fail找,一只找不到，则指向根结点)

以单模式串"ababac"为例:(蓝色为fail指针)(相当于kmp算法的AC自动机)

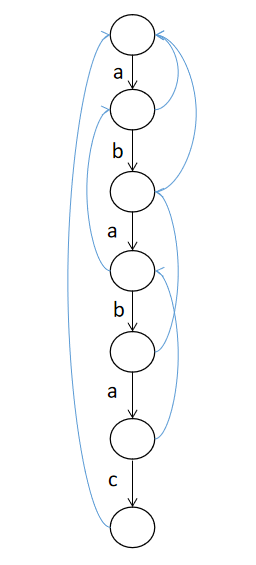
板子题

以一道题目给出写出模版:
P3808 【模板】AC自动机（简单版）

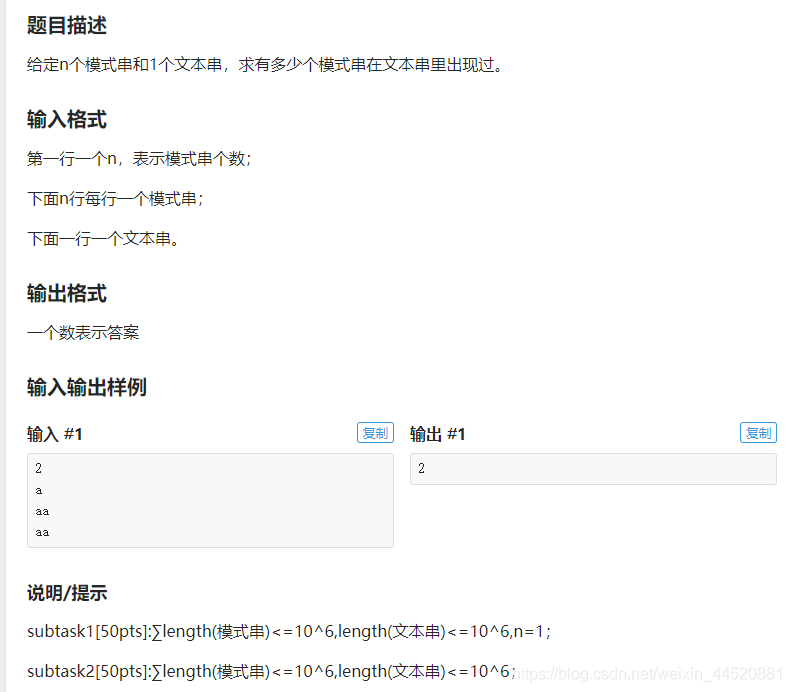
AC代码:

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;const int maxn = 1000006;	//结点个数 struct Aho{struct trienode{int next[26];int fail=-1;int cnt=0;	//是否匹配到模式串 }ac[maxn];queue<int> que;int ac_num=1;void init(){	//自动机初始化 for(int i=0;i<maxn;i++){memset(ac[i].next,0,sizeof(ac[i].next));ac[i].fail = ac[i].cnt = 0;}ac[0].fail = -1;ac_num = 1;}void insert(char *word) {int p = 0;int size = strlen(word);for(int i=0;i<size;i++){char c = word[i];if(ac[p].next[c-'a']==0)ac[p].next[c-'a'] = ac_num++;p = ac[p].next[c-'a'];}ac[p].cnt++;return;}void build(){ac[0].fail = -1;que.push(0);while(!que.empty()){int p=que.front();que.pop();for(int i=0;i<26;i++){if(ac[p].next[i]!=0){int p2 = ac[p].fail;while(p2!=-1){if(ac[p2].next[i]!=0){ac[ac[p].next[i]].fail = ac[p2].next[i];break;}p2 = ac[p2].fail;}if(p2==-1) ac[ac[p].next[i]].fail = 0; que.push(ac[p].next[i]);}}}return;}int query(char *words){int n = strlen(words);int res=0;int p = 0;for(int i=0;i<n;i++){char c = words[i];if(ac[p].next[c-'a']!=0)p = ac[p].next[c-'a'];else{p=ac[p].fail;while(p!=-1&&ac[p].next[c-'a']==0)p = ac[p].fail;if(p==-1) p = 0;else p = ac[p].next[c-'a'];}for(int p2=p;p2!=-1&&ac[p2].cnt!=-1;p2=ac[p2].fail){res+=ac[p2].cnt;ac[p2].cnt = -1;	//此处是一个优化点！ }}return res;}
}aho;char p[1000006];
int main(){int n;scanf("%d",&n);for(int i=0;i<n;i++){	//输入模式串scanf("%s",p);aho.insert(p);}aho.build();scanf("%s",p);printf("%d",aho.query(p));return 0;
}

使用指针构建结点但是无法AC的代码

自己检查了很多遍找不到错误啊啊啊啊啊，把测试样例下载下来数据跑不起来，修改了N遍对照两个代码结果都一样啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊！但是第二个测试样例死活就是过不去啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;struct Aho{struct trienode{trienode* next[26]={NULL};trienode* fail=NULL;int cnt;	//是否匹配到模式串 }*root=new trienode();queue<trienode*> que;void insert(char *word) {trienode *p = root;int size = strlen(word);for(int i=0;i<size;i++){if(p->next[word[i]-'a']==NULL)p->next[word[i]-'a'] = new trienode();p = p->next[word[i]-'a'];}p->cnt=1;return;}void build(){while(!que.empty()) que.pop();que.push(root);while(!que.empty()){trienode* p=que.front();que.pop();for(int i=0;i<26;i++){if(p->next[i]!=NULL){trienode* p2 = p->fail;while(p2!=NULL){if(p2->next[i]!=NULL){p->next[i]->fail = p2->next[i];break;}p2 = p2->fail;}if(p2==NULL) p->next[i]->fail = root; que.push(p->next[i]);}}}return;}int query(char *words){int n = strlen(words);int res=0;trienode *p = root;for(int i=0;i<n;i++){char c = words[i];if(p->next[c-'a']!=NULL)p = p->next[c-'a'];else{p=p->fail;while(p!=NULL&&p->next[c-'a']==NULL) p = p->fail;if(p==NULL) p = root;else p = p->next[c-'a'];}for(trienode* p2=p;p2!=NULL&&p2->cnt!=-1;p2=p2->fail){res+=p2->cnt;p2->cnt = -1;	//此处是一个优化点 }}return res;}
}aho;char p[1000006];
int main(){int n;scanf("%d",&n);for(int i=0;i<n;i++){	//输入模式串scanf("%s",p);aho.insert(p);}aho.build();scanf("%s",p);printf("%d",aho.query(p));return 0;
}