本文主要是介绍qq一笔画红包 的c语言解决方法(改),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我之前的程序采用邻接矩阵存储图链接如下,我这里稍作改进
https://blog.csdn.net/eu_zero/article/details/112056006
考虑到稀疏图用类似于邻接表的方式来输入可以节约用户的输入时间,于是我改进了代码,新增一个in()函数采用类似邻接表的录入形式,内部存储形式不变依旧用邻接矩阵存储图。
顺手修复了对于边数较少的图无法实现一笔画的bug
#include <stdio.h>
//节点从1开始编号
#define MAXSIZE 20
typedef struct edgeStack
{int from;int to;
}Edge;Edge VisitStack[100]={0};
Edge PathStack[100]={0};
int VTop=-1,PTop=-1,SumEdges=0;void Invisit(int from,int to)
{VTop++;VisitStack[VTop].from=from;VisitStack[VTop].to=to;
}
void Inpath(int from,int to)
{PTop++;PathStack[PTop].from=from;PathStack[PTop].to=to;
}
void Outvisit()
{VTop--;
}
void Outpath()
{PTop--;
}
int Visit(int from,int to) //边未走过则返回1
{int i=0;for(i=0;i<=VTop;i++){if(VisitStack[i].from==from && VisitStack[i].to==to) return 0;if(VisitStack[i].from==to && VisitStack[i].to==from) return 0;}return 1;
}
void find(int edges[][MAXSIZE],int v)
{int i=v,j=0;for(j=1;j<=MAXSIZE;j++){if(Visit(i,j)&&edges[i-1][j-1]==1) //判断是否走过这条边并且是否有边存在{Invisit(i,j);Inpath(i,j);printf("%d ",i);find(edges,j); //递归访问下一个节点}}if((PTop+1<SumEdges)&&(j>MAXSIZE)) Outpath();
}
int search(int edges[][MAXSIZE])
{int i=0,j=0;for(i=0;i<MAXSIZE;i++){for(j=0;j<MAXSIZE;j++){SumEdges+=edges[i][j];}}SumEdges=SumEdges/2; //求出总边数,用于之后判断是否遍历完成for(i=1;i<=MAXSIZE;i++){VTop=-1; //换第一个节点的时候需要清零栈PTop=-1;printf("以%d为第一个点: ",i);find(edges,i);printf("\n");if(PTop+1>=SumEdges) return 1;}return 0;
}
void in(int edges[][MAXSIZE],int v)
{char ch=0;int num=0,i=0,j=0;int a[MAXSIZE]={0};while((ch=getchar())!='\n'){if( ch<='9' && ch>='0'){num=num*10+(ch-'0');}else if(ch=' '){a[i++]=num;num=0;}}if(num==0) return; //如果该点没有邻接点,避免对邻接数组的改动a[i]=num;for(j=0;j<=i;j++){edges[v-1][a[j]-1]=1;}printf("邻接矩阵更新为:\n");for(i=1;i<=MAXSIZE;i++){for(j=1;j<=MAXSIZE;j++){printf("%d ",edges[i-1][j-1]);}printf("\n");}
}
int main()
{int edges[MAXSIZE][MAXSIZE]={0};int i=0,j=0;printf("请一次输入与每一个顶点邻接的顶点编号,空格隔开,回车结束\n");for(i=1;i<=MAXSIZE;i++){printf("与%d点邻接的顶点序列:",i);in(edges,i);}if(search(edges)){printf("\n成功完成一笔画,一种解法为: ");printf("%d ",PathStack[0].from);for(i=0;i<=PTop;i++){printf("%d ",PathStack[i].to);}printf("\n");}else printf("该图无法一次走过所有边,无法一笔画\n");
}
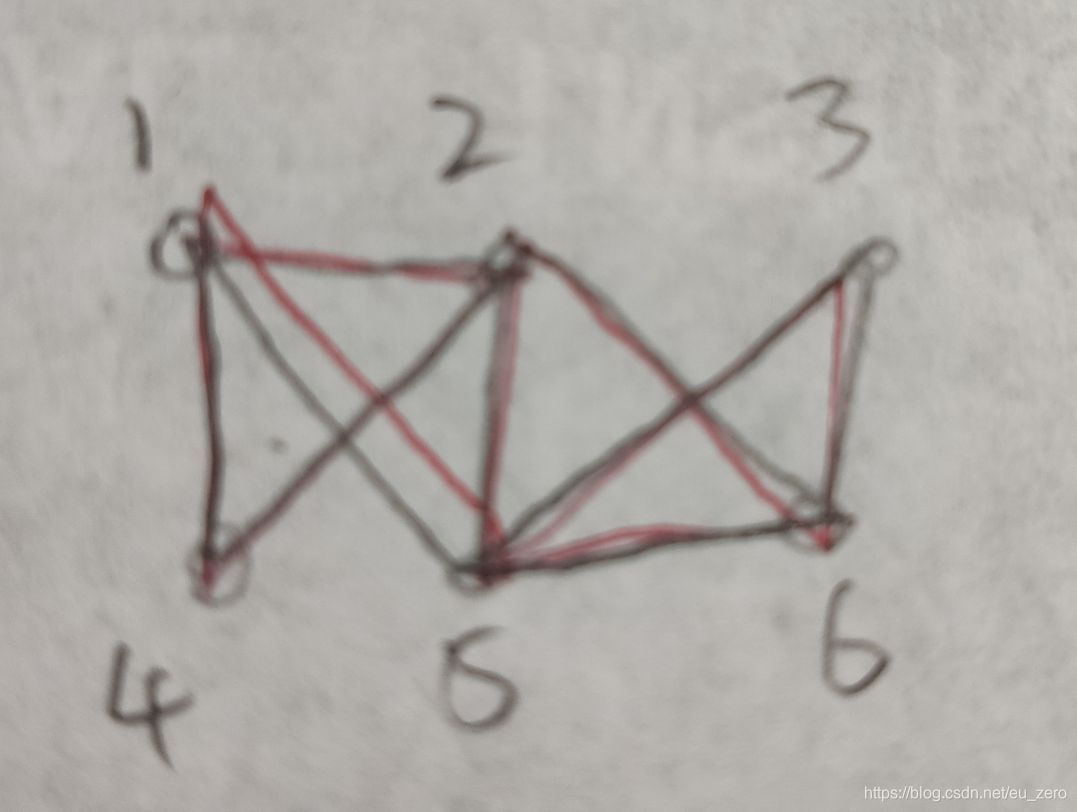

这篇关于qq一笔画红包 的c语言解决方法(改)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



