图论知识——欧拉回路(一笔画问题) Hierholzer方法

许多题目看起来是模拟，其实应该抽象为数学模型，寻找效率更高的解题方法
前置知识：
欧拉回路不等于欧拉路径，AB BC CA构成欧拉环路ABCA,符合题意。AB BC CD构成欧拉路径ABCD，也符合题意。
https://blog.csdn.net/qq_34454069/article/details/77779300
https://blog.csdn.net/qq632544991p/article/details/51097077
题目：https://www.luogu.org/problemnew/show/P1341
题解
https://blog.csdn.net/stillxjy/article/details/51956183
https://blog.csdn.net/binling/article/details/51742845
https://blog.csdn.net/binling/article/details/51742845
Hierholzer :
在本题中，n个无序字母对构成n+1长度的欧拉回路或欧拉字母对，那么只要通过度来判定是欧拉回路或者欧拉路径，那么只要找到起始点就一定可以简单的通过DFS找出该路径。
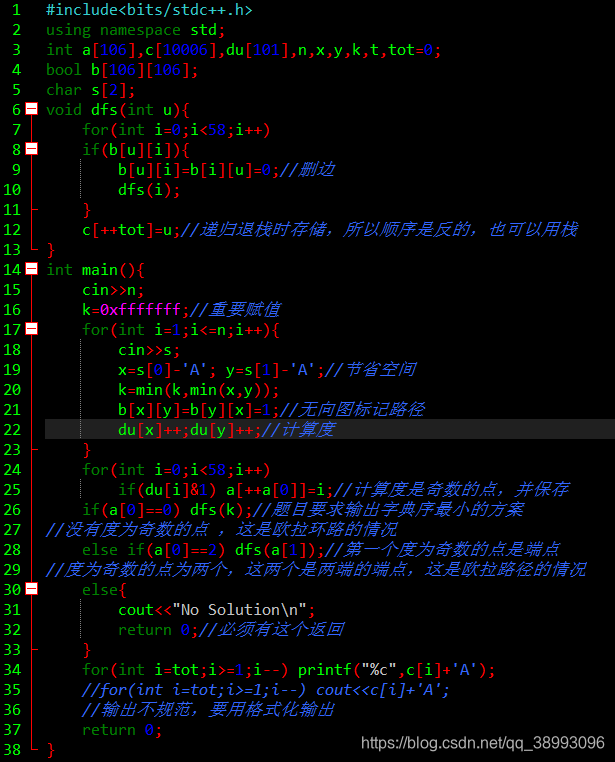
写法一：

#include<bits/stdc++.h>
using namespace std;
int a[106],c[10006],du[101],n,x,y,k,t,tot=0;
bool b[106][106];
char s[2];
void dfs(int u){for(int i=0;i<58;i++)if(b[u][i]){b[u][i]=b[i][u]=0;//删边 dfs(i);}c[++tot]=u;//递归退栈时存储，所以顺序是反的，也可以用栈 
}
int main(){cin>>n;k=0xfffffff;//重要赋值 for(int i=1;i<=n;i++){cin>>s;x=s[0]-'A'; y=s[1]-'A';//节省空间 k=min(k,min(x,y));b[x][y]=b[y][x]=1;//无向图标记路径 du[x]++;du[y]++;//计算度 }for(int i=0;i<58;i++)if(du[i]&1) a[++a[0]]=i;//计算度是奇数的点，并保存 if(a[0]==0) dfs(k);//题目要求输出字典序最小的方案 
//没有度为奇数的点 ，这是欧拉环路的情况 else if(a[0]==2) dfs(a[1]);//第一个度为奇数的点是端点 
//度为奇数的点为两个，这两个是两端的端点，这是欧拉路径的情况else{cout<<"No Solution\n";return 0;//必须有这个返回 }for(int i=tot;i>=1;i--) printf("%c",c[i]+'A');//for(int i=tot;i>=1;i--) cout<<c[i]+'A';//输出不规范，要用格式化输出return 0;
}

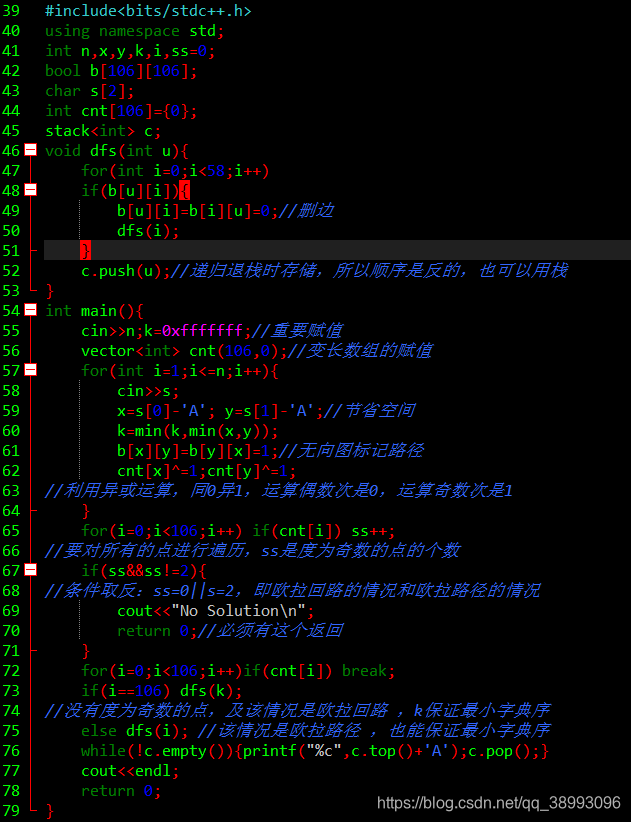
写法二：

#include<bits/stdc++.h>
using namespace std;
int n,x,y,k,i,ss=0;
bool b[106][106];
char s[2];
int cnt[106]={0};
stack<int> c;
void dfs(int u){for(int i=0;i<58;i++)if(b[u][i]){b[u][i]=b[i][u]=0;//删边 dfs(i);}c.push(u);//递归退栈时存储，所以顺序是反的，也可以用栈 
}
int main(){cin>>n;k=0xfffffff;//重要赋值 vector<int> cnt(106,0);//变长数组的赋值 for(int i=1;i<=n;i++){cin>>s;x=s[0]-'A'; y=s[1]-'A';//节省空间 k=min(k,min(x,y));b[x][y]=b[y][x]=1;//无向图标记路径 cnt[x]^=1;cnt[y]^=1;
//利用异或运算，同0异1，运算偶数次是0，运算奇数次是1 }for(i=0;i<106;i++) if(cnt[i]) ss++; 
//要对所有的点进行遍历，ss是度为奇数的点的个数 if(ss&&ss!=2){
//条件取反：ss=0||s=2，即欧拉回路的情况和欧拉路径的情况 cout<<"No Solution\n";return 0;//必须有这个返回 }for(i=0;i<106;i++)if(cnt[i]) break; if(i==106) dfs(k);
//没有度为奇数的点，及该情况是欧拉回路 ，k保证最小字典序 else dfs(i); //该情况是欧拉路径 ，也能保证最小字典序 while(!c.empty()){printf("%c",c.top()+'A');c.pop();}cout<<endl;return 0;
}