Leetcode---370周赛

本文主要是介绍Leetcode---370周赛，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目列表

2923. 找到冠军 I

2924. 找到冠军 II 

2925. 在树上执行操作以后得到的最大分数 

2926. 平衡子序列的最大和

一、找到冠军I 

 

第一题模拟题，简单来说是看每一行(列)是否全是1，当然不包括自己比自己强的情况，需要特判

代码如下

class Solution {
public:int findChampion(vector<vector<int>>& grid) {int n=grid.size();for(int i=0;i<n;i++){int j;for(j=0;j<n;j++){if(i!=j&&grid[i][j]==0){break;}}if(j==n)return i;}return -1;}
};

二、找到冠军II

这题和上题相似，但是所给的数据内容不同。只要看图中是否只有一个结点的入度为0就行

代码如下

class Solution {
public:int findChampion(int n, vector<vector<int>>& edges) {vector<int>deg(n);for(auto&e:edges){int y=e[1];deg[y]++;}int ans=-1;for(int i=0;i<n;i++){if(!deg[i]){if(ans!=-1)return -1;ans=i;}}return ans;}
};

三、在树上执行操作以后得到的最大分数

 

这题的题目意思是让这棵树的每条路径和都>0，同时让自己获得的分数最大

如果正着思考，我们就要考虑选哪些点，使得我们获得的分数最大，同时保持树的健康，这样思考无论是从上往下走，还是从上往下走，我们都要去考虑遍历到的结点的上下两边的情况，比较麻烦

那么正难则反，如果我们逆着思考，即考虑选哪些结点留在树上，那么我们就可以边遍历，边找最小值，然后用 总价值 减去 留在书上的最小值 得到答案

代码如下

class Solution {typedef long long LL;
public:long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {int n=values.size();vector<vector<int>>g(n);for(auto&e:edges){int x=e[0],y=e[1];g[x].push_back(y);g[y].push_back(x);}//该dfs函数用来计算一棵树的每条路径上的最小值之和function<LL(int,int)>dfs=[&](int x,int fa)->LL{LL res=0;for(int y:g[x]){if(y!=fa){res+=dfs(y,x);}}return res==0?values[x]:min((LL)values[x],res);//如果res=0说明是叶子节点，直接返回结点值};LL s=accumulate(values.begin(),values.end(),0LL);return s-dfs(0,-1);}
};

四、平衡子序列的最大和

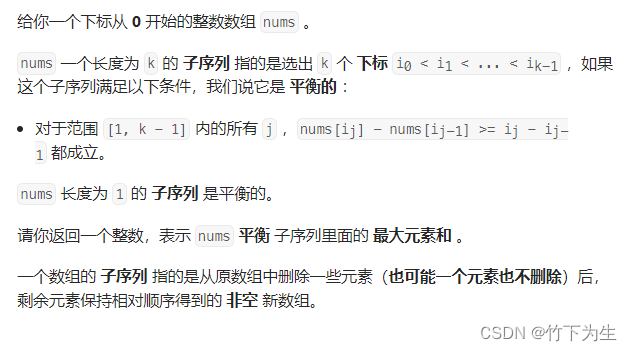
正常来说，求子序列的最大元素和，用动态规划就行，这题有点特殊，需要优化时间复杂度，我们先来看看正常的动规的写法

思路：将题目给的不等式移项，得到num[ i ] - i >= nums[ j ] - j，这样我们就将两个相互影响的值，变成了只和自己有关的nums[i]-i，我们用数组b存放nums[i] - i

动规：

dp数组含义：dp[i]表示以i为结尾的最大元素和

递推公式：dp[i]=max(dp[j]，0)+nums[i]        条件  j<i && b[j]<=b[i]

初始化具体在代码，答案为max(dp[i])

class Solution {
public:typedef long long LL;long long maxBalancedSubsequenceSum(vector<int>& nums) {int n=nums.size();LL ans=INT_MIN;vector<LL>dp(nums.begin(),nums.end());for(int i=0;i<n;i++){for(int j=i-1;j>=0;j--){if(nums[i]-i>=nums[j]-j)dp[i]=max(dp[j]+nums[i],dp[i]);}ans=max(dp[i],ans);}return ans;}
};

上面代码的时间复杂度是O(n^2)，数据范围太大，过不了，那么如何优化时间复杂度？

上面代码最浪费时间的是 dp[i]=max(dp[j])+nums[i] 这行代码，即查找最大值速度慢了，那么我们怎么才能提高查找的速度？这里就要引入一个数据结构---树状数组，它其实和线段树相似，是线段树的"子集"。

如果没听过的，可以去了解一下，这里不具体讲它的原理

(这里推荐一个视频，讲得很简洁明了：五分钟丝滑动画讲解 | 树状数组_哔哩哔哩_bilibili )

树状数组适合维护前缀和/前缀最大值+单点更新这类题目，更新和查询的时间复杂度均为O(logn)

而求 max(dp[j]) 不就是维护前缀最大值吗？每当计算出一个dp[i]，就去更新树状数组，简直完美

现在还有一点需要注意：我们怎么样去将b[i]和树状数组的下标映射起来，这里又有一个知识点：离散化【复制+排序+去重】具体看代码（这个就是几行代码的事，很简单的）

(这里有人可能会对将b[i]和树状数组的下标映射这点感到疑惑，因为我们上面分析的是对dp数组的前缀最大值进行维护才对，解释一下：我们的递推公式有两个条件，j<i && b[j]<=b[i]，我们是从左往右遍历的，所以更新到树状数组中的值全部满足j<i的情况，即我们只要考虑b[j]<=b[i]这个条件就行，那么我们对b数组排序之后，映射到树状数组的下标后，自然就满足这个条件了，我们只要在比b[i]小的b[j]元素对应的dp[i]中求最大值就行，即求前缀最大值)

代码如下

typedef long long LL;
class BIT{    vector<LL>bit;
public:BIT(int n):bit(n,LLONG_MIN){}void updata(int i,LL data){while(i<bit.size()){bit[i]=max(bit[i],data);i+=(i&-i);}}LL pre_max(int i){LL res=LLONG_MIN;while(i>0){res=max(res,bit[i]);i&=(i-1);}return res;}
};
class Solution {
public:long long maxBalancedSubsequenceSum(vector<int>& nums) {int n=nums.size();vector<int>b(n);//离散化//1.复制for(int i=0;i<n;i++)b[i]=nums[i]-i;//2.排序sort(b.begin(),b.end());//3.去重b.erase(unique(b.begin(),b.end()),b.end());LL ans=LLONG_MIN;BIT tree(n+1);for(int i=0;i<n;i++){int j=lower_bound(b.begin(),b.end(),nums[i]-i)-b.begin()+1;//计算下标LL data=max(0LL,tree.pre_max(j))+nums[i];tree.updata(j,data);ans=max(ans,data);}return ans;}
};

这篇关于Leetcode---370周赛的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---