本文主要是介绍【自用】图像压缩感知(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
二维图像重建
- 1 相关原理
- 1.1 最速下降法求解TV最小化
- 1.2 基于距离驱动的正/反投影模型
- 2 USP-2DTV算法实现
- 参数声明
- 算法步骤
- 动态松弛因子 + 图像质量评估
1 相关原理
1.1 最速下降法求解TV最小化
最速下降法基本思想是在每次迭代过程中,选取一个合适的步长,使得目标函数的值能最大程度的减小。
使用图像的TV范数作为梯度下降算法的目标函数来重构图像。
在(一)中已经说明压缩感知框架下的重建模型转化为有约束的TV最小化问题:
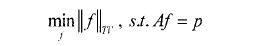
上式可以转化为无约束的最小化问题:
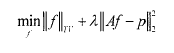
L2范数为通常意义上的模(函数的绝对值的平方的积分的平方根)。
执行梯度下降算法需要首先表示出图像TV范数的梯度。该梯度也可以认为是一幅图像,其中每个像素值是图像的TV范数对该点像素的偏导数。
故||fTV||对每个像素值求偏导获得一个单调表达式,使用下式近似导数:
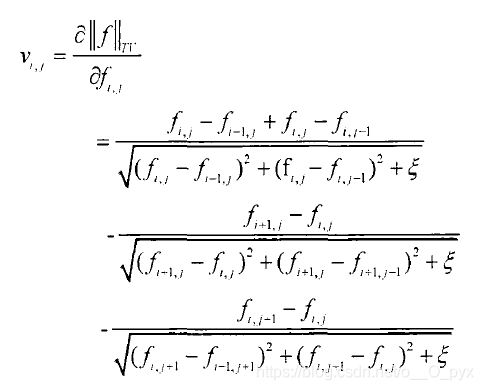
其中,ξ是为了防止分母出现0值而设置的一个常数,取ξ=10^-6。
在实际应用中,梯度计算仅应用在图像非边缘的像素点。将得到的梯度向量称为ν,与图像向量f一样,各元素可以由单个索引νs或像素索引νi,j表示。最速下降算法的迭代更新公式为:

其中,α为步长因子,用来控制收敛速度。在每一步的迭代中,从点fi,j(n)出发,沿着梯度的负方向展开一维搜索,确定新的迭代点fi,j(n+1)。
1.2 基于距离驱动的正/反投影模型
Wf将图像从图像域映射到投影域,也称为正投影。
WTp(WT是W的转置或伴随矩阵)将投影数据从投影域反映射到图像域,称为反投影。
系统矩阵W将图像域与投影域联系起来。更一般地说,系统矩阵W=(ωmn)MxN有MxN个元素。ωmn称为加权系数,表示第n个像素对第m个检测器单元的相对贡献。因此,与每个检测器单元相关的加权系数在系统矩阵中组成一行。类似地,与每个像素相关的加权系数在系统矩阵中组成一列。
在迭代重建方法中,迭代地应用正投影和反投影运算根据目标函数来近似最符合投影数据的图像。系统矩阵也考虑了许多因素,如系统几何和衰减过程等。为了确定系统矩阵元素,必须选择一个系统模型,也称为正/反投影模型。系统模型在迭代重建过程的效率和重建精度方面起着重要的作用:系统模型很大程度上决定了重建的准确性,只有在系统矩阵本身准确的情况下解才是准确的;此外,迭代重建需要基于系统模型迭代地重新计算系统矩阵元素,这是迭代重建算法的主要计算成本。
主流的投影/反投影模型主要分为三类:像素驱动模型(PDM)、射线驱动模型(RDM)和距离驱动模型(DDM)。
- 基于PDM的方法是指主循环是图像像素索引。这种方法通常用于FBP重建的反投影实现[44-46]。简单的基于PDM的线性插值方法很少用于正投影,因为它会在投影域引入高频伪影[47-48]。
- 基于RDM的方法是指主循环是检测器元素索引。这种方法基本上用于正投影操作。通常,基于RDM的方法中的加权系数可以通过两种方式来确定。第一种是将加权系数定义为投影射线与图像像素之间的相交长度[44,48,49]。另一种方法是通过插值,例如线性插值或双线性插值,在靠近投影射线的图像像素之间定义加权系数[46,50]。射线驱动方法在反投影中很少使用,因为它容易在图像域引入高频伪影[47,53]
方法一:
Herman.GT.ImageReconstructionfromprojections[M].1980.
ZengGGullbergG.Aray-drivenbackprojectorforbackprojectionfilteringandfilteredbackprojectionalgorithms[J].IEEENuclearScienceSymp.MedicalImagingConf.(SanFrancisco),1993:1199-201.
SiddonRL.Fastcalculationoftheexactradiologicalpathlengthfora three-imensionalCTarray[J].MedicalPhysics,1985.12(2):252-255.方法二:
ZhuangW,GopalSS,HebertTJ.Numericalevaluationofmethodsforcomputing tomographicprojections[J].IEEETransactionsonNuclearScience,1994,41(4):
1660-1665.
JosephPM.AnImprovedAlgorithmforReprojectingRaysthroughPixelImages[J].IEEETransactionsonMedicalImaging.1982.1(3):192-196.
- 目前最先进的是DDM[47,51,52],它结合了一种高度顺序的存储器访问模式,算法复杂度相对较低。同时它综合了PDM和RDM的优点,能够既避免了图像域伪影,又避免了投影域伪影,可以用于正投影和反投影过程。
距离驱动的正投影过程:将每个检测器单元的边界和感兴趣行的像素边界映射到X轴上,在所有像素边缘和检测器单元边缘与公共轴的交叉点上循环,计算两个相邻交叉点之间的间隔长度,并使用这些长度来确定相应像素对相应检测器单元的贡献。

为了正确模拟线积分,和Joseph算法的处理相同,将衰减系数除以投影角度的余弦值,并乘以像素尺寸。首先将重建图像作一定角度的旋转,使得在几何关系上射线与Y轴的夹角范围始终在[-45,45]内,然后以X轴为公共轴,将像素边缘和检测器边缘映射到公共轴上。像素投影到某检测器时,对该检测器单元的投影值贡献为:

其中,S为该检测器单元的投影值,μN为当前像素单元的灰度值,t为像素纵向尺寸,α为投影角度,o为图像像素映射到X轴与检测器映射到X轴的重叠部分长度,w为检测器单元映射到X轴的长度,如图所示。
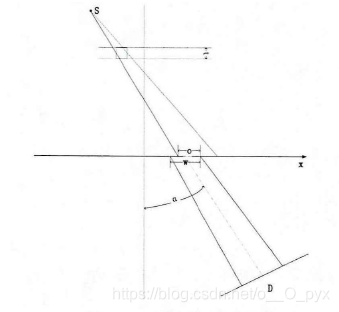
2 USP-2DTV算法实现
基于DDM的迭代求解线性方程组的粗略重建模块(简称DD模块),基于最速下降法的TV范数最优化模块(简称TV模块)。
DD模块
- DATA-步骤,基于距离驱动的正/反投影迭代更新重建图像,使重建图像的投影数据与原始投影数据一致
- POS-步骤,确保图像像素值的非负性
TV模块
- BLAN-步骤,计算平衡因子,结果作为梯度下降的自适应下降步长因子
- GRAD-步骤,基于梯度最速下降法最小化估计图像的TV范数,迭代更新重建图像
参数声明
- 总迭代次数 n 、DATA子循环次数 m 、GRAD子循环次数 k
- DATA-step迭代中,用f(DATA) [n,m]表示第n次总体迭代的第m次DATA子迭代中的图像向量,W为投影矩阵,距离驱动的投影模型不需要遍历整幅图像和整个监测器,仅遍历在公共轴上有重叠的部分计算所需的投影矩阵元素。
- 用f(POS) [n]表示第n次总迭代的POS-step中投影到负半平面的估计图像。
- 用dA[n]表示第n次总迭代的BLAN-step中计算得到的平衡因子。
- GRAD-step迭代中,用f(GRAD) [n,k]表示第n次总体迭代的第k次GRAD子迭代中的图像向量。
- 投影数据向量 p

算法步骤
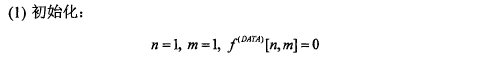
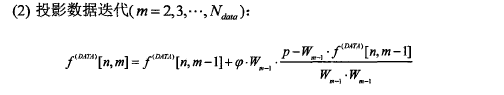
其中,φ=λω,λ为松弛因子,ω是一个自适应松弛因子矫正参数,与当前子循环次数和投影矩阵元素相关。
系统矩阵W=(ωmn)MxN有MxN个元素。ωmn称为加权系数,表示第n个像素对第m个检测器单元的相对贡献
正投影 -》与投影数据作差 -》 反投影 -》松弛矫正 -》 叠加到图像像素
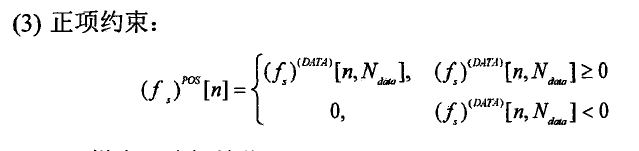


(6)初始化下一次循环:
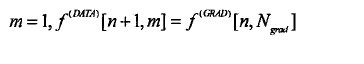
返回步骤(2)继续迭代运行。如果n达到迭代停止条件,即停止迭代,将重建图像保存并显示。
注意:

动态松弛因子 + 图像质量评估
这篇关于【自用】图像压缩感知(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









