MBA-day18 数学-应用题-集合问题-应用题

1 基础知识点

1.1 两个集合

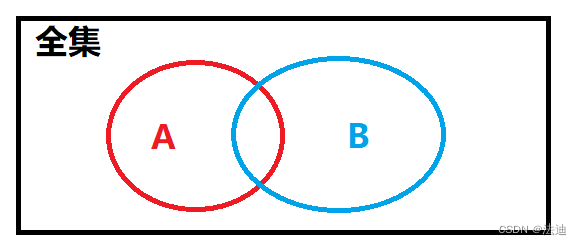
公式： A ∪B= A + B- A∩B

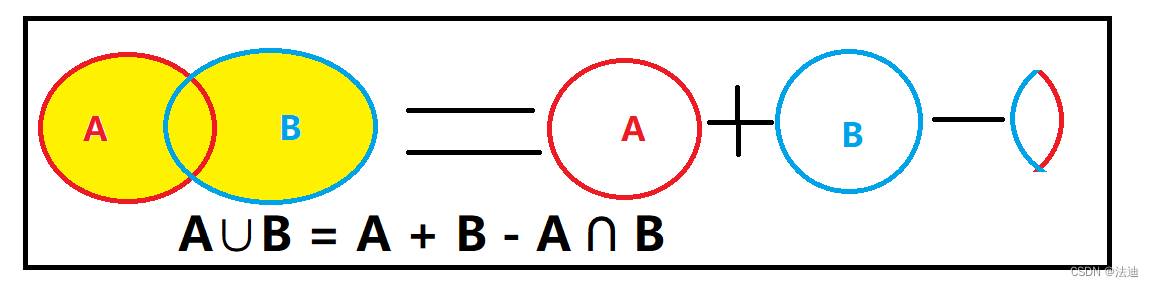
从上图可以看出为什么需要 减去（A∩B）, 因为 A 就包含一份 （A∩B）， B 也包含一份（A∩B），故重复了一份，需要去除重复，就可以得到 A ∪B=的图像面积了

• ∪表示至少有一个发生

1.2 三个集合

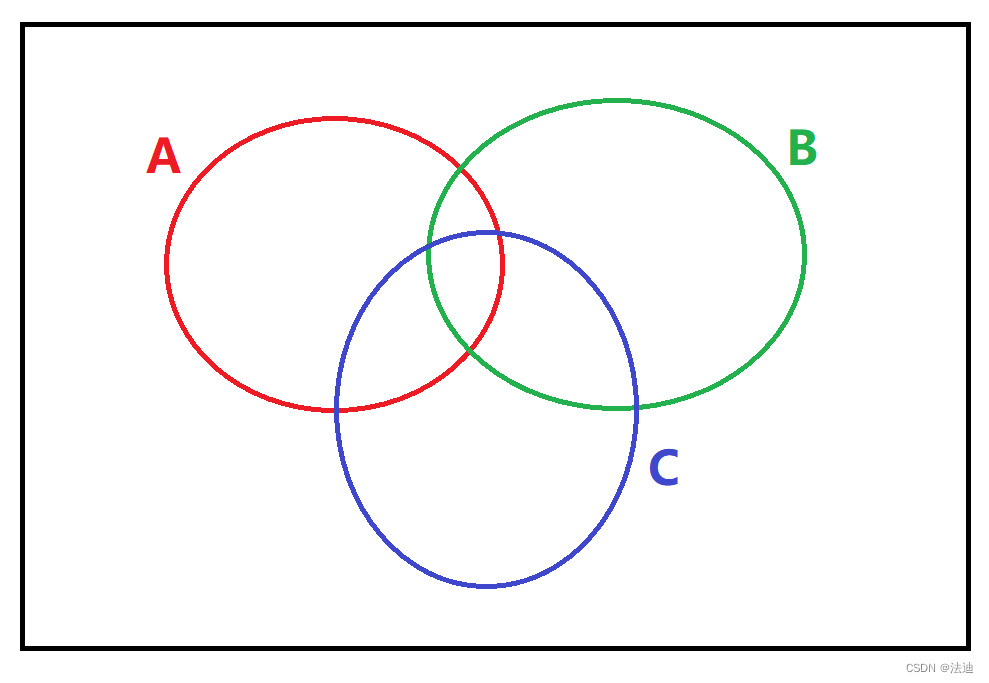
• A ∪ B ∪ C = A + B + C - (A ∩ B + B ∩ C + A ∩ C) + A ∩ B ∩ C
• A ∪ B ∪ C = 只有1个+只有2个+只有3个
• A + B + C = 只有1个+2只有2个+3只有3个

1.2.1 A ∪ B ∪ C = A + B + C - (A ∩ B + B ∩ C + A ∩ C) + A ∩ B ∩ C

将上述的并集合关系，转化成求ABC得面积就行，当成图像来理解就行

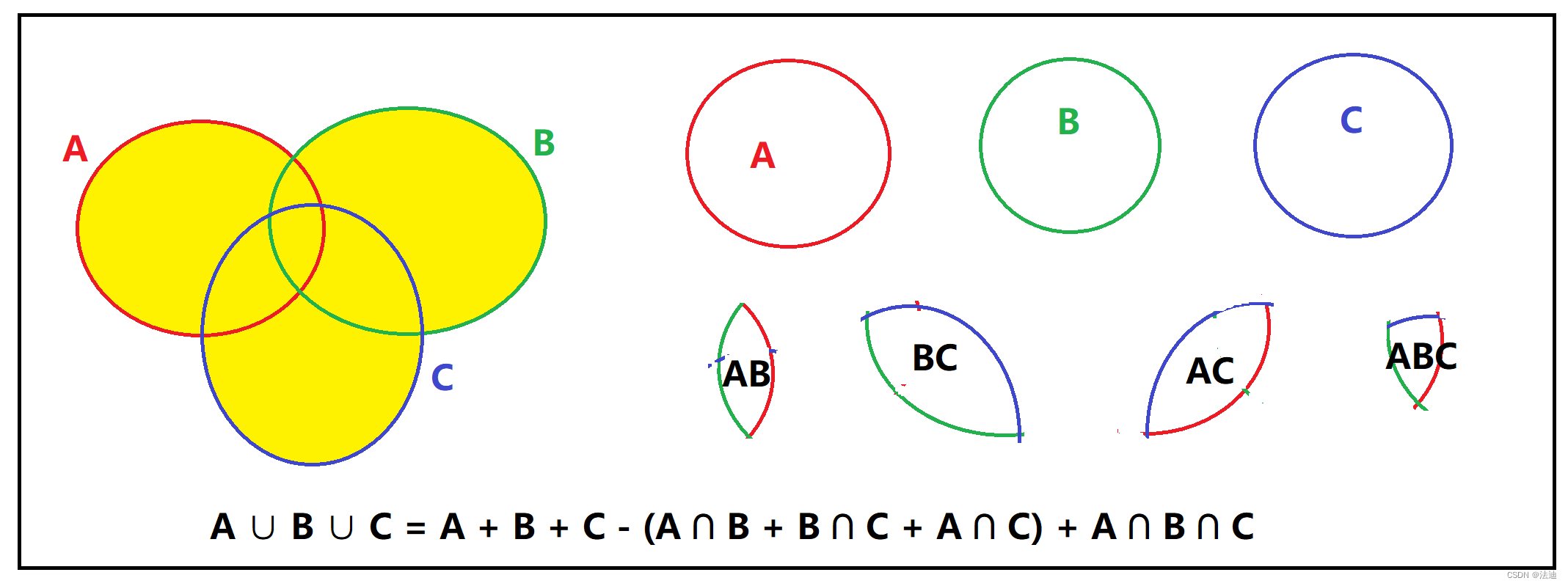
• ∪表示至少有一个发生

1.2.2 A ∪ B ∪ C = 只有1个+只有2个+只有3个

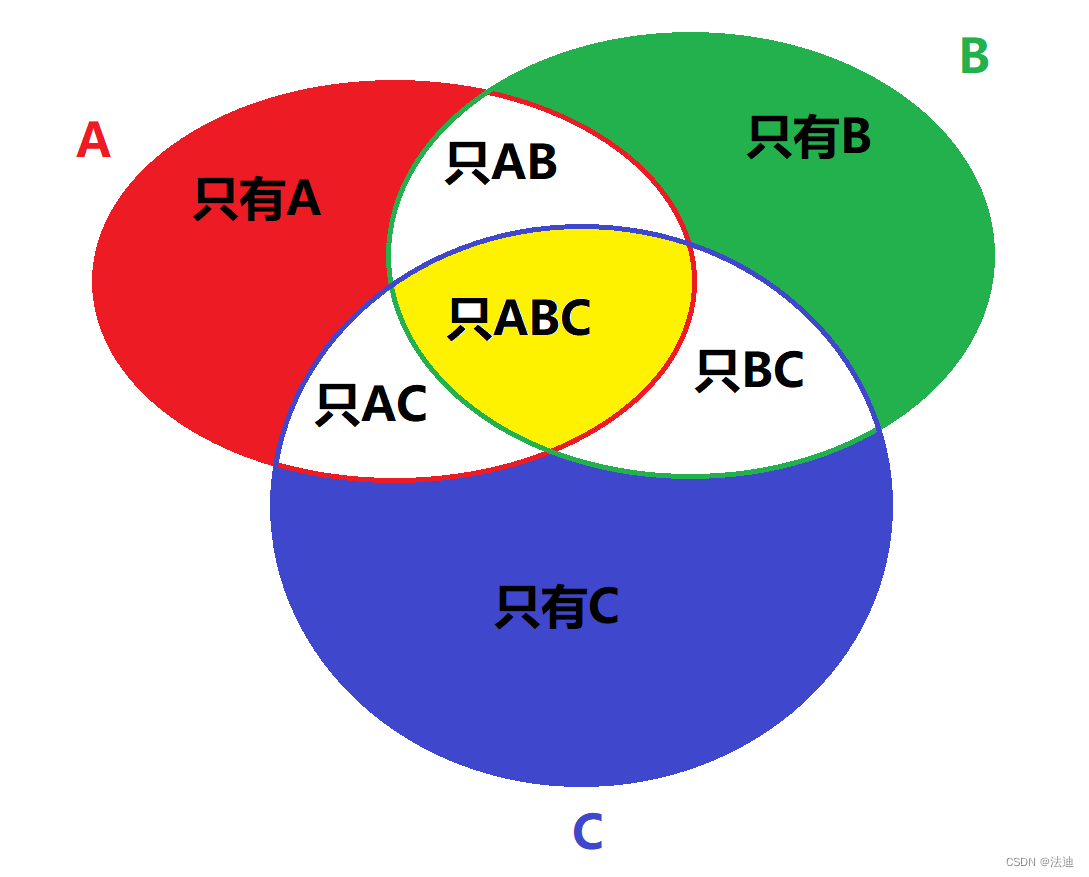
A ∪ B ∪ C = 只有1个+只有2个+只有3个
= 只有A + 只有B + 只有C

• 只有AB + 只有AC + 只有BC
• ABC

标志：至少有1个发生，出现只有

1.2.3 A + B + C = 只有1个+2只有2个+3只有3个

A 的面积 = 只有A + 只有AB + 只有AC + ABC
B 的面积 = 只有B + 只有AB + 只有BC + ABC
C 的面积 = 只有C + 只有AC + 只有BC + ABC

A + B + C = 只有1个+2只有2个+3只有3个

标志：只有, A = , B= , C=

2 应用题

2.1 例题 1

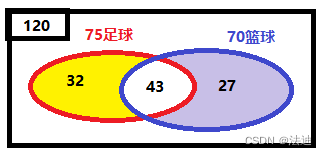
对120人进行一次兴趣调查，喜欢足球运动的人数为75，喜欢篮球的为70，只喜欢足球的人有32，求只喜欢篮球的人
答：27

2.2 例题 2

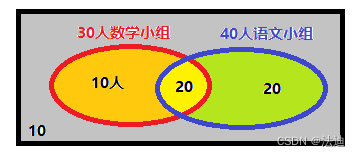
某年级学生参加数学小组有30人，参加语文小组的有40人，有10人只参加数学小组，10人两个小组都为参加，求该年级共有学生？
答：10人只数学+20人只语文+20人数学和语文+10人都不参加 = 60

2.3 例题 3

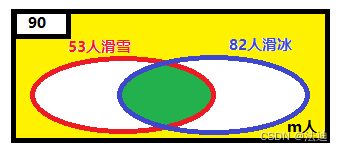
某高校志愿者90人去支援某次冬运会，53人到滑雪场地，82人到滑冰场地，有m人两个场地都没去，则两个场地都去的有51人。
1）m = 10
2) m = 6

答：条件2充分，但条件1不充分

解：
A ∪B=90-m
A ∪B=  A  +  B-  A∩B故 53+82-51 = 90-m
84=90-m
m=6

2.4 例题 4

小王和小李参加同一次趣味知识问答，两人都答对的题目为20道，每道题都至少有一个人答对，则题目总数为36道。
1）小王答对29道，小李答对27道
2）小李答对27道，小王答对两人都答对题目数的5/4

答：条件1充分，但条件2不充分

1）小王答对29道，小李答对27道，条件1充分

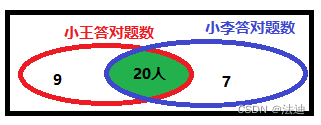
2）小李答对27道，小王答对两人都答对题目数的5/4，条件2不充分
小李答对27道，小王答对两人都答对题目数的5/4*20 = 25，相当于总题目：5+20+7 = 33

2.5 例题 5

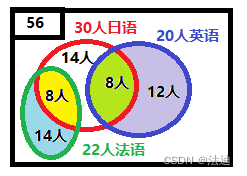
在外国语学院，某班共有56名学生，其中有30人会日语，有22人会法语，有20人会英语，同时，没有三种语言都会，也没有三种语言都会的人，则只会法语的有14人
1）会日语又会英语有8人
2）会日语又会法语8人

参考答案为：条件1充分，条件2不充分

2.6 例题 6

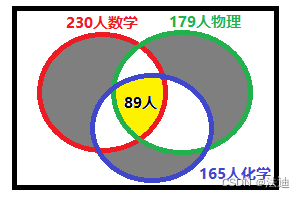
某年级先后举行数理化三科竞赛，学生中参加数学的有203人，参加物理的有179人，参加化学的有165人，只参加一科的有140人，三科都参加的有89人，求参加竞赛的总人数？

答： 参加竞赛的总人数 299 人

解：
参加数学= 只参加数学 + 参加数物 + 参加数化 + 参加三科
参加物理= 只参加物理 + 参加数物 + 参加物化 + 参加三科
参加化学= 只参加化学 + 参加数化 + 参加物化 + 参加三科203 + 179 + 165 = （只参加数学+只参加物理+只参加化学）+ 3（参加三科）+ 2（参加数物+参加数化+参加物化）
547 = 140 + 3 * 89 + 2（只参加两科）
140=2（只参加两科）
只参加两科=70人参加竞赛总人数=只参加1科 + 只参加2科 + 只参加3科 = 140 + 70 + 89 = 299 人