本文主要是介绍致我们终将忘记的算法(说不清道不明的排序),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1->插入排序:
插入排序的思想很简单,将待排序的元素,从后往前在已经排序好的部分序列中寻找要插入的位置。
Code:
void InsertSort(int Array[]){
for(int i=1;i<Array.Size();i++){
int tmp=Array[i];
int j=i-1;
while(j>=0 && Array[j]>tmp) {Array[j+1]=Array[j]; j--;}
Array[j+1]=tmp;
}
}
如果目标是将n个元素的序列升序排列,那么插入排序在n个序列已经是升序的情况下,只需要n-1次比较操作。若初始序列是降序的情况,那么需要n*(n-1)/2次比较,另外插入排序的数值赋值操作是比较操作的次数减去(n-1)次。插入排序的平均时间复杂度为O(n^2),是稳定的排序算法。
2->二分插入排序
对于插入排序的重点是查找和插入,若将上述的查找过程,换成二分查找的算法,就形成了二分插入排序算法。
void BinaryInsertSort(int A[]){
for(int i=1;i<A.size();i++){
int Key=A[i] , low=0 , high=i-1;
while(low<=right){
int mid=(low+high)/2;
if(A[mid]>Key) high=mid-1;
else low=mid+1;
}
/*退出循环之后,low即是要插入的位置*/
for(int j=i-1;j>=low;j--) A[j+1]=A[j];
A[low]=Key;
}
}
二分插入排序是一种稳定的排序。插入每个记录需要比较O(log i)次,最大移动i+1次。最佳的情况时间复杂度为O(nlogn),最差和平均的复杂度均为O(n^2).
3->希尔排序
希尔排序是属于插入类排序算法。对于插入排序平均时间复杂度为O(n^2),但是在序列基本有序的情况下可以将时间复杂度提高到O(n).希尔排序就是利用了这一特点。
希尔排序的思想:先将整个待排序记录序列分割成若干个子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对整个序列进行一次直接插入排序。
另外希尔排序的子序列构成不是简单的分段分割,而是将相隔某个“增量”的记录组成一个子序列。
void ShellInsert(int A[],int dk){
for(int i=dk;i<A.size();i++){
int j=i-d; int tmp=A[i];
while(j>=0 && A[j]>tmp){A[j+d]==A[j];j-=d;}
A[j+d]=tmp;
}
}
void ShellSort(int A[]){
int dk=A.Size()/2; //初始增量,为数组长度的一半
while(d>=1){
ShellInsert(A,dk);
dk=dk/2;
}
}
希尔排序是不稳定的排序算法,它的平均时间复杂度为O(n^2).在希尔排序中选取不同的步长,会有一个不同的时间复杂度。
4->简单选择排序算法
一趟简单选择排序的操作:通过n-i次关键字间的比较,从n-i+1的记录中选择最小的记录,与在i位置的记录交换。
void SelectSort(int A[],int n){
for(int i=0;i<n;i++){
int min=i;
for(int j=i+1;j<len;j++)
if(A[min]>A[j]) min=j;
/*交换*/
if(min!=i) swap(a[min],a[i]);
}
}
简单的选择排序的交换次数在0到n-1次之间。比较次数为n(n-1)/2与初始序列无关。无论最好还是最坏的情况时间复杂度都为O(n^2)
5->冒泡排序
冒泡排序算法思想:比较相邻的两个元素,如果次序不对则交换它们。对每一对相邻元素做同样的工作。直到最后一对。那么最后一个元素应该是有序的。
void BubbleSort(int A[],int n){
int i=n;
while(i>0){
for(int j=0;j<i-1;j++)
if(A[j]>A[j+1]) swap(A[j],A[j+1]);
i--;
}
}
冒泡排序的最优的时间复杂度为O(n),是一种稳定的排序算法。平均时间复杂度为O(n^2);
6->快速排序
快速排序的基本思想:通过一趟排序将记录分割成独立的两个部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整体有序。
void Partition(int A[],int low,int high){ //一趟排序过程
int pivotKey=A[low];
while(low<high){
while(low<high && A[high]>=pivotKey) --high;
A[low]=A[high];
while(low<high && A[low]<=pivotKey) low++;
A[high]=A[low];
}
A[low]=privotKey;
return low;
}
void QSort(int A[],int low,int high){
if(low<high){
int mid=Partition(A,low,high);
QSort(A,low,mid-1);
QSort(A,mid+1,high);
}
}
快排是不稳定的排序算法,最坏的情况时间复杂度为O(n^2),平均时间复杂度为O(nlogn).
7->堆排序
要了解堆排序,首先要了解下面几个问题:
a):堆是怎么定义的?在堆排序里面提到的堆一般指的是二叉堆:满足性质,父结点的键值总是大于或者等于(小于或者等于)任何一个子节点的键值。每个结点的左右子树都是一个二叉堆。
b):堆调整:堆调整是为了保持堆的性质而进行的一些操作。对某一节点为根的子树做堆调整,其实就是将该根节点“下沉”一直沉到合适的位置。
例如:对于最大堆的堆调整:
1,在对应的数组元素A[i]、左孩子A[Left(i)]、右孩子A[Right(i)]中最大的那个标记为max;
2,如果A[i]已经是最大的元素,则程序结束。
3,否则将A[i]与子节点当中最大的那个交换
4,再从交换的子节点开始,重复1,2,3步骤,直到叶子节点
一次堆调整的时间复杂度为log(n).
c):如何建堆:建堆是一个通过不断的堆调整,使得整个二叉树满足堆的性质的操作。在数组中的话,我们一般都是从下标为n/2的数开始做堆调整,直到下标为0的数满足堆的性质。
d):如何进行建堆:堆排序在上述(c)中对数组建堆的操作之后,第一次将A[0]与A[n-1]交换,再对A[0]到A[n-2]进行堆调整,一直重复直到A[0]与A[1]交换,就形成了一个有序数组
void HeapAdjust(int A[],int s,int m){ //使s到m之间成为一个大顶堆
int tmp=A[s];
for(int j=2*s ;j<=m;j*=2){
if(j<m && A[j]<A[j+1]) j++;
if(tmp>A[j]) break;
A[s]=A[j]; s=j;
}
A[s]=tmp;
}
void HeapSort(int A[]){
for(int i=A.size()/2;i>=0;i--) HeapAdjust(A,i,A.size()); //建堆的过程
for(int i=A.size()-1;i>1;i--){ //堆排序的过程
swap(A[0],A[i]);
HeapAdjust(A,0,i);
}
}
堆排序的最差最优以及平均时间复杂度都为O(nlogn).空间复杂度为O(1),堆排序是不稳定的排序算法。
8->归并排序
算法思想:假设初始序列含有n个记录,则可以看成有n个有序子序列,每个子序列的长度为1,然后两两归并,得到n/2个长度为1或者2的子序列,重复上述过程,直到得到一个长度为n的有序序列为止。
void Merge(int A&[],int B[],int k,int m,int n){ //将B[k----m]和B[m+1-----n]合并存入A数组
for(int i=k,j=m+1;i<=m && j<=n;k++){
if(B[i]>B[j]) A[k]=B[j++]; else A[k]=B[i++];
}
if(i<=m) A[k...n]=B[i...m]; if(j<=n) A[k...n]=B[j....n];
}
void MSort(int A&[], int B[],int s,int t){
if(s==t) A[s]=B[s];
else{
int mid=(s+t)/2;
Msort(C,B,s,mid);
Msort(C,B,mid-1,t);
Merge(A,C,s,m,t);
}
}
归并排序是稳定的排序算法,时间复杂度为O(nlogn)
9->计数排序
计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数,然后根据数组C来将A中的元素排序到正确的位置,它只能多整数进行排序。
它是一种稳定的排序算法。正常情况时间复杂度会达到O(n).
10->基数排序
基数排序是一种非比较型整数排序算法,其原理是将整数按位切割成不同的数字,然后按照每个位分别比较。
算法的过程:
将所有待比较数值(正整数)统一为同样的数位长度,数位较短的前面补0;从最低位开始,依次进行一次排序;这样从最低位直到最高位完成以后就变成了一个有序数列。
基数排序的时间复杂度为O(k*n)
11->桶排序
桶排序也称为箱排序。工作原理:将数组分到有限数量的桶子里面。每个桶再个别排序(有可能采用其他方法对桶进行个别排序,也有可能继续递归的进行桶排序)
桶排序是稳定的,大多数是常见排序里面最快的一种,比快排还要快,确定就是太耗费内存空间。
算法描述:
设置一定量的数组当作空桶子
遍历待排序数列,把每个数放到相应的桶中。
对于每个不是空的桶进行子排列
归纳总结:
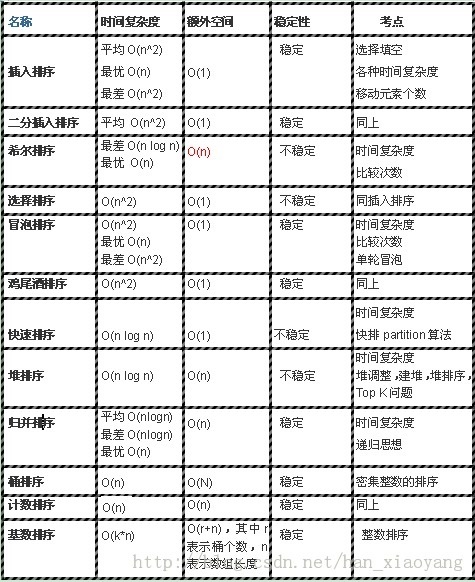
这篇关于致我们终将忘记的算法(说不清道不明的排序)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







