PID（二）P、I、D三个参数的感性认识（小白入门）

PID（二）P、I、D三个参数的感性认识（小白入门）

上一篇从PID整体是干啥的，整体的层面感性的分析了一下，考虑到P、I、D三个参数对大部分入

门的人也是挺不和谐的，这篇就应粉丝的留言要求，从三个参数各自的角度巴拉巴拉。

PID结构图

PID公式

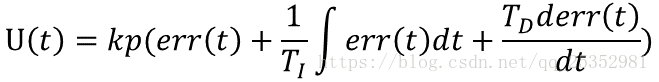
O、引入场景

故事是这么着的，很久以前我是一年级的时候，看到一只乌鸦正在往瓶子里衔石子，一看就想要喝水。乌鸦衔了一会，停下来了，绕着瓶子再看，似有思考的痕迹。我也在想，乌鸦想啥呢。后来我想到了。

一、P 比例算法

首先，瓶子里的水高0.2，加石子，等液面上升到离瓶口a的时候，乌鸦可以喝到水，且a较小（下文为方便称此液面为瓶口）。我们假设距瓶口为a的液面高度为1.0，故事开始了 。

一开始，水面离瓶口误差为err=0.8,乌鸦衔石头的大小与err成正比，故大小u=kperr,我们尝试着取kp=0.5，那么
第一次：u=0.50.8=0.4，液面达到0.6的位置；
第二次：u=0.5*0.4=0.2，液面达到0.8的位置；
……
第N次：液面会相当接近1.0，乌鸦就可以喝到水。

这边会有一个小小的误差，而且随着次数的增加还在减小，我们叫它暂态误差，只要次数足够多，就可以足够小，小到无伤大雅。

这就是P的作用，我们把液面图连续的画出来就是这样
假如没有P,我们看到
石子的大小是相等的，没有调整，最后可能超过目标值。

二、 I 积分算法

上面只是乌鸦想的，等它衔了两块后，发现，石头之间会有空隙，不会排出水量。哦，乌鸦太难了。
鉴于此，我们简化一下，假设每丢一个石子会占掉0.1的水，这个水在空隙中就排不出来了。

还用上面的方法算
第一次：u=0.50.8=0.4-0.1=0.3，液面到达0.5的位置；
第二次：u=0.50.5=0.25-0.1=0.15，液面到达0.65的位置；
……
第N次：液面到了0.8的位置；
第N+1次：u=0.5*0.2=0.1-0.1=0，就是说我们不用加石子了，但液面只能到0.8的位置。

这是什么原因？

我们看到，这个时候液面已经稳定了，我们叫这个误差为稳定误差。

这个误差挺大的，我们想个办法解决一下。

I 算法 u=kperr+ki（对err积分)

我们取ki=0.5
第N+1次：u=0.50.2+0.50.2=0.2-0.1=0.1，液面达到0.9；（忽略前面的误差，从这次开始对误差进行积分，足以说明问题）
第N+2次：u=0.50.1+0.5（0.2+0.1）=0.25-0.1=0.15，液面达到1.05；
第N+3次：u=0.5*（-0.05）+0.5*（0.2+0.1+（-0.05））=0.1-0.1=0，液面刚好达到1.05;
第N+4次：u=0.5*（-0.05）+0.5*（0.2+0.1+（-0.05）+（-0.05））=0.075-0.1=-0.025，液面达到1.025；
第N+N次：液面一直在瓶口附近震荡，震荡越来越小。

我们看到，又经过N次的操作，水面最终从0.8到达瓶口附近很小的范围内 ，这是积分算法对比例算法的补充；
但这中间会出现震荡，就是液面会在瓶口附近波动，这是积分算法带来的问题。

三、D 微分算法

添加了积分的乌鸦已经能够把液面弄到1.0附近的地方，但中间出现了一个问题，在第N+2次加石子后，水撒了出来，那么乌鸦能够喝的水就少了。它是一只倔强的乌鸦，怎能允许这样的事发生，奥里给，解决它。

蛋黄的长裙，蓬松的头发，呦，我就是你身边最美的乌鸦。

加入微分项
u=kperr+ki(对err积分)+kd*(对err微分)

我们取kd=0.5

第N+1次：u=0.50.2+0.50.2+0.5*(0.2/1)=0.3-0.1=0.2，液面刚好达到1.0；
第N+2次：u=0.50 +0.5（0.2+0）+0.5*（0/1）=0.1-0.1=0，液面稳定在1.0.
第N+3次：u=0.50 +0.5（0.2+0+0）+0.5*（0/1）=0.1-0.1=0，液面稳定不动。

说实话，这个例子相当巧合，带入太完美了
但完全不妨碍说明问题

我们可以看到，加入微分项的乌鸦，准确无误的将液面控制在瓶口，有效的解决了积分项带来的震荡。（参数取得好，就是这么骚<_<）

##凌晨1点了，明早6点老爹又该叫着跑步了，太难了，想开学呐，超级超级想呐/哭唧唧

这篇的算式有点多，但都是相当简单的，微分、积分都用离散 我错了，都用简单的式子代替了，后面会再写一篇从工程角度分析的文章，还请大佬指正呐/抱拳/抱拳