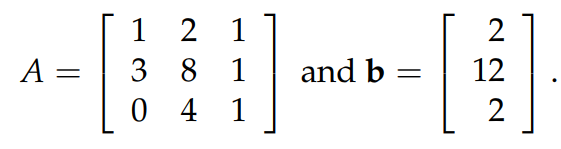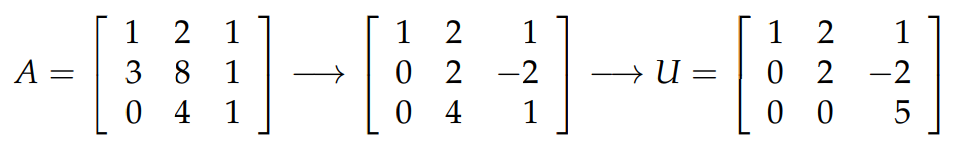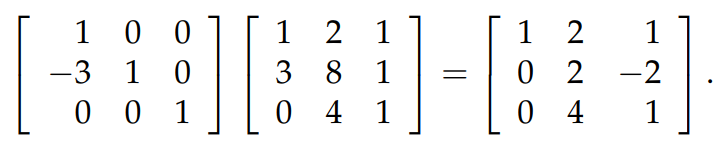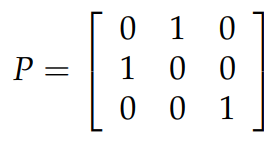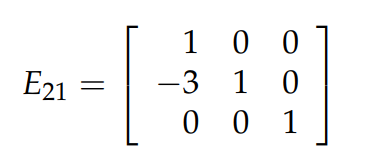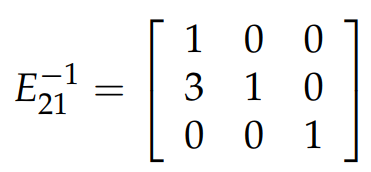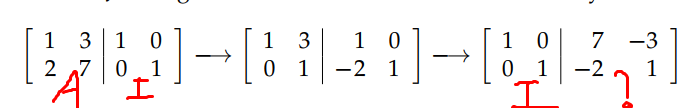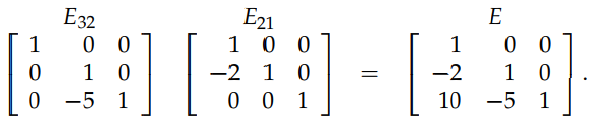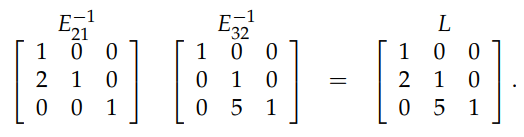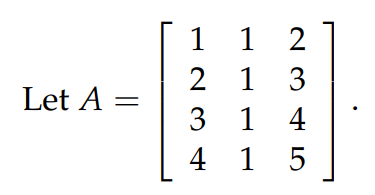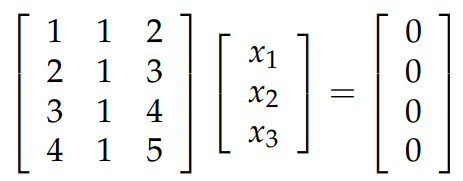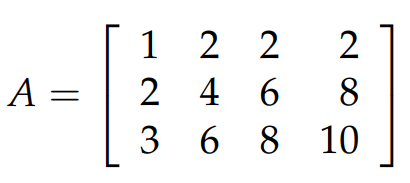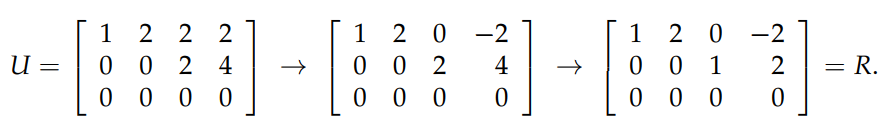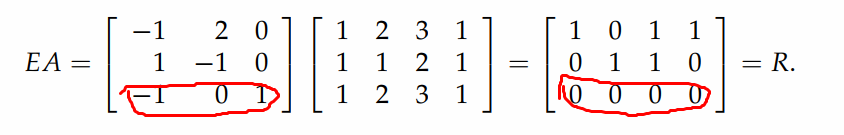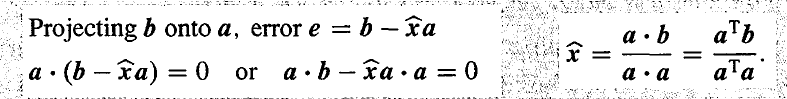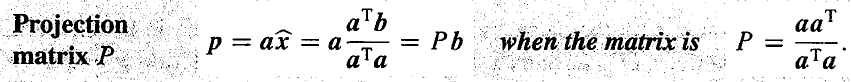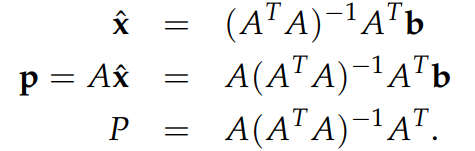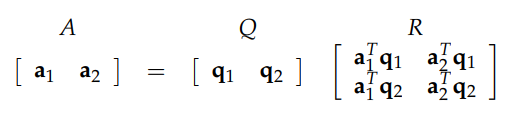本文主要是介绍MIT 18.06 线性代数总结(Part I),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Overview
本文是对 MIT 18.06 的总结。下面3幅图来自 MIT Course 18.06 的 course overview slides.
Fall 2017 Lecture Summaries
The Geometry of Linear Equations
教授在这个 lecture 中介绍了3个概念:Row Picture,Column Picture, and Matrix Picture,其中理解 Column Picture 是最重要的。
我们可以把线性方程组写成矩阵的形式,Row Picture 描述的是从矩阵的 row 看起,对于每一个 row 来说,在 2D 中可以决定一条直线,在 3D 中决定一个平面; 而对于 Column Picture 来说,从 column 看起,形成了列向量的 linear combination,因此在 2D 和 3D 中都是向量,只不过2者之间相差一个维度而已; Matrix Picture 没什么好说的。详情可以看 The Geometry of Linear Equations.
Given a matrix A , can we solve:
If the answer is “no”, we say that
从几何上理解会更直观一些。比如在空间中有3个向量(A,B,C),如果 A 和 B 通过 linear combination 会得到 C,因此 C 在向量 A 与 B 组成的平面上,因此这3个向量的 linear combinations 不能 fill 整个3维空间。在进一步,如果这3个向量共线,那么它们就只能 fill 一条直线。
Elimination with Matrices
在文章开头,已经看到了线性方程组可以写成矩阵的形式。下图中就是把一个3元方程组写成矩阵的形式(Ax=b):
在高中的时候,如果想要求解出这样的方程组,需要不断地化简消元,只不过我们现在用更加系统的方法去做这件事情,道理本身是一样的。这里直接操纵矩阵,从而达到消元的目的。过程如下图所示:
由于对方程的左边(即矩阵 A)进行了上述步骤的简化,同样的步骤也需要应用到向量 b 上。应用到 b 以后,我们得到了一个新的向量 c=⎡⎣⎢26−10⎤⎦⎥ ,因此整个消元方法转换 Ax=b 到 Ux=c,通过 back substitution 就可以得到这个3元方程组的解了。
在上面的消元过程中,pivots may not be 0. If there is a zero in the pivot position, we must exchange that row with one below to get a non-zero value in the pivot position. If there is a zero in the pivot position and no non-zero value below it, then the matrix A is not invertible.
熟悉了上面的消元过程,现在让我们了解一下 Elimination Matrices 的概念。在上面消元的第一步中,我们是把矩阵 A 的 row 2 - 3×row 1,通过下图中的方式也可以达到同样的效果:
上图中最左面的矩阵就是消元矩阵。The elimination matrix used to eliminate the entry in row m column
A permutation matrix exchanges two rows of a matrix. 对于一个 n×n 的矩阵来说,可以有 n! 种方式交换行,因此就有 n! 个permutation matrix,这些矩阵形成了一个组. 单位矩阵就是一个 permutation matrix 的例子,只不过它不交换任何行而已。关于 permutation matrix 的规律,就是你怎样交换单位矩阵的行,你就如何交换另一个应用到它的矩阵的行。比如对于下图中的 permutation matrix 来说,它交换了单位矩阵的行1和行2,如果你把这个 permutation matrix 应用到另一个矩阵上,那么它就会交换那个矩阵的第1行和第2行。
既然我们有 n! 种方式交换行,无论你怎么交换都逃不出这些可能。因此,无论你对同一个矩阵应用多少个 permutation matrix,交换之后的结果一定在 n! 种情况内。因此可以得出,当你从一组 permutation matrix 中拿出任意多个矩阵时,它们的乘积也一定在组里。
接下来我再谈一下关于 elimination matrix 的逆矩阵。比如下图中的 elimination matrix,它的目的是进行操作: row 2 - 3×row 1,为了 “undo” 这个操作,我们必须进行操作: row 2 -+3×row 1,即用 E21 的逆矩阵:
Multiplication and Inverse Matrices
有5种 perspective 来看矩阵的乘法:它们分别是:row times column,columns,rows,column times row,blocks. 关于它们的详情参考 矩阵乘法。
接下来谈一谈如何判断 square matrix A 是否可逆。设矩阵 Ax=0,如果你可以找到一个非0的 x 使其成立,则 A 不可逆。这是为什么呢?假设 A−1 存在,且有一个非0解 x. 由于 A−1(Ax)=A−10=0≠x=Ix=(A−1A)x ,违背了假设,所以矩阵 A 不可逆。
接下来谈一谈当一个矩阵可逆的时候,如何用 Gauss-Jordan Elimination 来求出它的逆矩阵。下图中就是整个过程(Once we have used Gauss’ elimination method to convert the original matrix to upper triangular form, we go on to use Jordan’s idea of eliminating entries in the upper right portion of the matrix)。
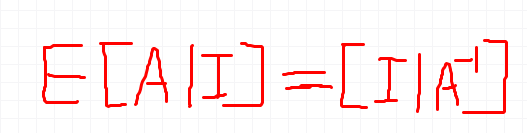
上面的消元过程很好理解,但是为什么上图中“问号”上面的矩阵就是 A−1 呢?在下图中通过把一个 elimination matrix E 应用到矩阵 A 上得到了单位矩阵 I,即 EA=I,所以 E= A−1 ,所以 EI= A−1I=A−1
Factorization into A = LU
正如本节标题所示,我们需要把矩阵 A 分解成2个矩阵(L 和 U)的乘积,where ‘LU’ stands for ‘lower upper’, and also called LU factorization. 在上面的小节中已经看到,通过对矩阵 A 的消元过程,最终可以得到一个 upper triangular 的矩阵 U,因此是 EA=U. 有了过程,我们就可以很容易把 A 分解成 LU 了。 E−1 EA= E−1 U,因此你会发现 L 实际上就是 E−1 .
矩阵 L 是 lower triangular 的,而且对角线上全是1. 你可以看每一步的消元矩阵,它都是对角线上是1,然后改变某个位置上的乘子。你可能会想,A=LU 和 EA=U,并没有什么太大区别吗!我们为什么更倾向于前者呢?举个例子一下就明白了。比如某个矩阵 A 的 A21 和 A32 两个元素需要消元,因此有下图中的2个消元矩阵。你会发现最终得到的 E 不仅在其需要消元的2个元素上有乘子,而且在左下角不还有个10出现,这就是副作用。
而对于通过求消元矩阵的逆,从而得到的 L 来说,如下图所示,它并没有这样的副作用。因此在没有行交换的情况下,消元矩阵中的乘子可以直接复制到 L 中。
当需要交换行时,我们可以写成:PA=LU,其中的 P 是 permutation matrix. 这种类型的矩阵有很好的性质: P−1=PT
A matrix A is symmetric if AT=A . Given any matrix R (not necessarily square) the product RTR is always symmetric, because (RTR)T=RT(RT)T=RTR
Vector Spaces
来自维基百科的定义:
A vector space (also called a linear space) is a collection of objects called vectors, which may be added together and multiplied (“scaled”) by numbers, called scalars.
通过上面的定义,我们可以判断一个给定的向量集合是否为 vector space. 比如,在 x-y 平面上第1象限的向量集合,它就不是 vector space. 集合中的任意2个向量相加依然在集合中,但是如果你乘上一个负数,得到的向量就不在集合中了。我们说这种类型的向量集合是 closed under addition but not under multiplication.
关于 subspace 的定义:
A vector space that is contained inside of another vector space is called a subspace of that space. Every subspace must contain the zero vector because vector spaces are closed under multiplication.
下面举2个例子:
The subspaces of R2
- all of R2
- any line through the origin
- the zero vector alone
The subspaces of R3
- all of R3
- any plane through the origin
- any line through the origin
- the zero vector alone
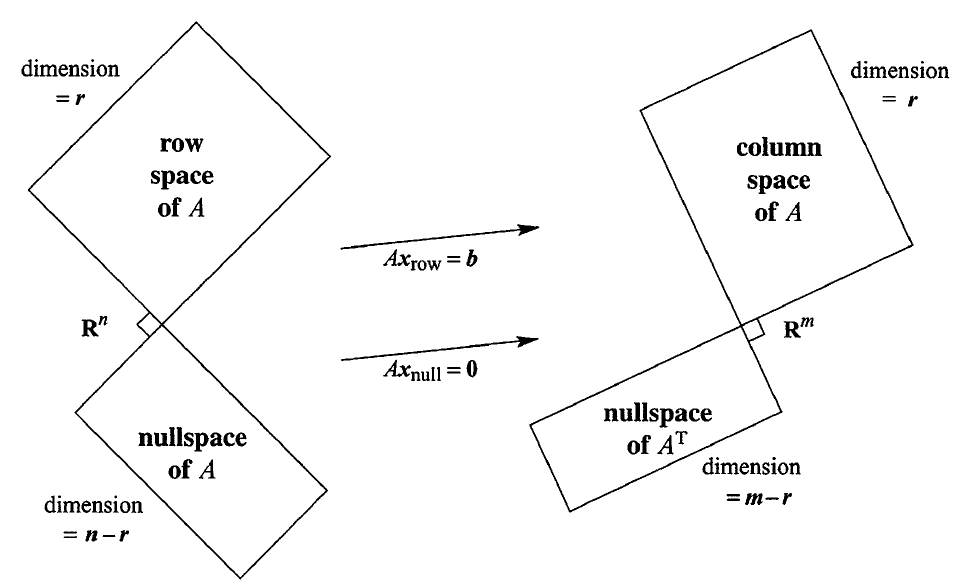
Column Space and Nullspace
对于一个 m×n 的矩阵 A 来说,column space 和 nullspace 是2个非常重要的 subspace,because they tell us a lot about the matrix A and solutions to Ax=b.
column space 的定义:
The column space of a matrix A is the vector space made up of all linear combinations of the columns of A.
从上面的定义可以知道,如果线性方程组 Ax=b 有解,那么向量 b 必须要在矩阵 A 的 column space 上。比如对于下图中的矩阵 A 来说,什么样的向量 b 可以使得 Ax=b 有解?不难发现,A 的第3列不是 independent 的,它是前2列的和,因此矩阵 A 的 column space 是4维枯空间中的 2D 的子空间,即一个过原点的平面。因此,只有在这个平面上的向量 b,我们才可以得到解。
nullspace 的定义:
The nullspace of a matrix A is the collection of all solutions x to the equation Ax = 0
你可能会想,nullspace 为什么会是 vector space 呢?我们假设 Ax=0 的解为向量 x; 这会导致 cx 也是解,因为 A(cx)=cAx=0; 同样道理 x1+x2 也会是解,因为 A(x1+x2)=Ax1+Ax2=0 。比如下图中的例子,我们一下就可以看出 x=⎡⎣⎢11−1⎤⎦⎥ 是其中的一个解,因此 cx 也会是解,所有的这些解构成了 nullspace,对于这个题目来说,nullspace 是三维空间中的一条过原点的直线。
Solving Ax = 0
上面我们已经介绍了一个矩阵的 nullspace 是什么,那么如何来计算出它呢?Khan 学院中的 Calculating the null space of a matrix 拿一个具体的例子来讲解找 null space 的过程。下面我来总结一下 MIT 课上介绍的方法,其实它们本质都是一样的。
那么如何求下图矩阵 A 的 null space 呢?首先,需要通过消元把矩阵 A 化简成 reduced row echelon form(它的 pivots 等于1,pivots 的上下全是0),在消元的过程中,它并不会改变 Ax=b 的解,因此就不会改变 null space.
下图中的消元过程使得矩阵 A 转化成了 U. 矩阵的 rank 等于它所拥有的 pivots 的数量,在这个例子中,rank=2. 我们把包含 pivot 的列叫做 pivot columns,剩下的列叫做 free columns,在我们这个例子中,第1和第3列为 pivot columns,第2和第4列为 free columns. 至此,我们已经把 Ax=0 的问题转换成了 Ux=0 的问题。
接下来,我们继续消元,把 U 化简成 reduced row echelon form,如下图所示。得到了 R 以后,我们就可以很容易地求出 null space 了。
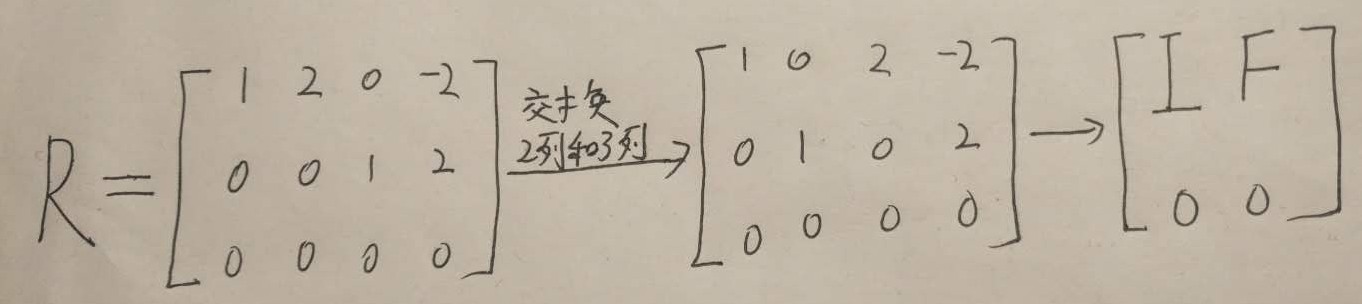
通过交换 R 中的一些列,我们可以把上面的 R 改写成下图所示的 block matrix. 上面已经说过了,这个矩阵的 rank 为2,而下图中的 I 是包含 pivot 的列,因此 I 是一个 2×2 的方阵; 由于总共的列数为4,free columns 为4-2=2,因此 F 为 2×2 的方阵。
有了上图中 R 的表示,相信大家不难写出 nullspace matrix N=[−FI] ,矩阵 N 中的 I 是 (n-r)×(n-r) 的方阵。因此我们最初想求的矩阵 A 的 null space 就是矩阵 N 的列的线性组合。计算机内部也是用这个算法来求的。
Solving Ax = b
上面小节中已经知道了如何求解 null space,即 Ax=0; 在这个小节中,我将总结如何求解 Ax=b. 在介绍如何求解之前,我们首先应该想到的是它是否存在解?如果存在的话,需要什么条件?如何求解?
不必多说,要想 Ax=b 有解,向量 b 一定在 column space C(A) 上。那么在存在解的情况下,我们如何找到全部的 solution 呢?首先,我们需要找出一个 particular solution,然后加上 nullspace 上的所有向量。如何找出 particular solution 呢?一种很自然的方法就是:把所有的 free variables 设置为0,然后求解 pivot 变量。而如何求出 nullspace 上面小节中已经介绍过了。
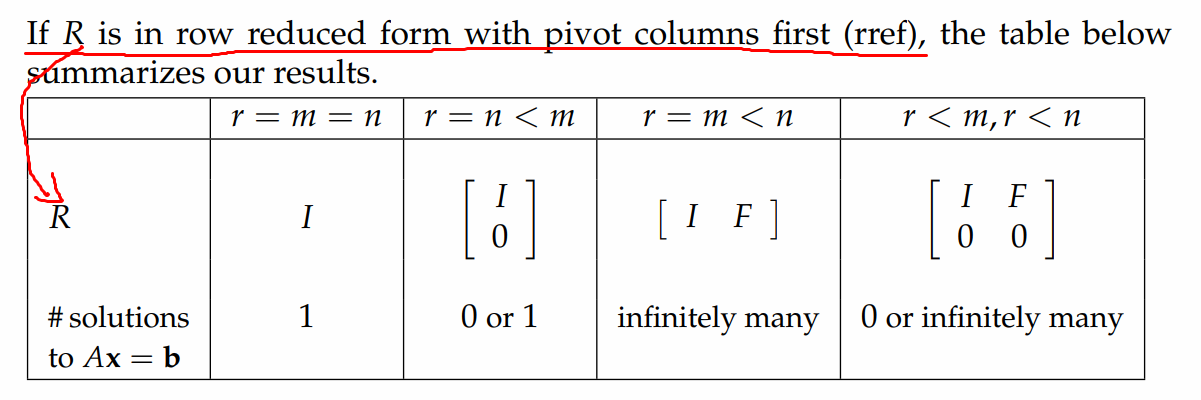
接下来,让讨论一下在什么情况下,才会有解。一个 m×n 的矩阵 rank r≤ min {m,n},下表总结了关于 rank 的4种情况,它们分别是:Full row and column rank,Full column rank,Full row rank,和 non-full rank 的情况。你可以通过 linear combinations 组合的方式来理解下表。举个例子,比如我有一个5×3的矩阵符合 Full column rank 的情况,那么第4行和第5行一定是前3行的 linear combinations(如果不懂,动手试一下这样的矩阵就全明白了),因此要想有解,向量 b 的第4和第5个 component 也一定要是前3个 component 的 linear combinations,满足这个条件有一个解,否则没有解。
因此,一个矩阵的 rank 告诉了你所有关于解的情况。详细信息可参考:Solving Ax = b: row reduced form R
Independence, Basis and Dimension
如果使 Ax=0 成立的解(即 null space)有 non-zero vector,这表明矩阵 A 中的某些列一定是另一些列的 linear combination,不然不可能有除去零向量以外的向量使等式成立。因此可以总结出:当一个矩阵的 null space 存在 non-zero 向量,那么矩阵 A 的这些列向量一定是 dependent 的; 反之,如果只有 zero 向量,那么就是 independent 的。
因此对一个 m×n 的矩阵 A 来说,消元过后发现它存在 free columns,即存在 free variables,这会导致我给以给 free variables 任意的值,然后求解出 pivot 变量的值。在这种情况下,你一定会找到 non-zero 的解,因此矩阵 A 是 dependent 的,并且它的 rank 一定是小于 n 的。另一方面,如果不存在 free columns,即没有 free variables,即矩阵 A 的所有列都是 pivot columns,你会发现除了 zero 向量可以使 Ax=0 以外,没有其它的向量可以做到,这是因为当你把矩阵 A 化简成 reduced row echelon form 时,并且全是 pivot columns,那么 A 化简的 R 一定是上面那么表格中的第1种情况或第2种情况,因此任何一个列的 linear combination 不可能得到另一些列,因此矩阵 A 的列是 independent 的,并且 rank 为 n.
Vectors v1,v2,⋯,vk span a space when the space consists of all combinations of those vectors. 比如:the column vectors of A span the column space of A. If vectors v1,v2,⋯,vk span a space S, then S is the smallest space containing those vectors. 比如,x-y 平面上的2个 independent 的向量 span 整个 x-y 平面的空间 S,即空间 S 包含这2个向量的所有 linear combinations. 而整个3维空间也包含这2个向量的所有 linear combinations,整个4维空间也包含,因此 S 是最小的包含这些向量的空间。
接下来谈一谈 basis 和 dimension. A basis for a vector space is a sequence of vectors v1,v2,⋯,vk with two properties:
- v1,v2,⋯,vk are independent
- v1,v2,⋯,vk span the vector space
其实很好理解,比如对于一个3维空间的 vector space 来说,它的 basis 一定由3个向量组成。如果有4个向量,那么多出来的这个向量是其它3个向量的 linear combination,因此这4个向量就不是 independent 的了; 如果是2个 independent 向量,那么你就只能形成一个3维空间中的一个2维的平面,因此这2个向量不能 span 整个3维的 vector space. 所以组成 basis 的向量不能多也不能少。
因此对于一个 Rn 的 basis 来说,它一定包括 n 个向量,每个向量有 n 个 component,如果把 basis 的这些向量放到一个矩阵中,即每个向量是矩阵的列向量,组成的这个矩阵一定是 invertible 的。反过来说,n vectors in Rn form a basis if they are the column vectors of an invertible matrix.
对于一个 Rn 的 vector space 来说,它的 basis 一定有 n 个向量组成,n因此这个 vector space 的 dimension 为 n.
如果明白了我上面总结的内容,你可以非常轻松地得出下面的结论:对于一个矩阵 A 来说:
1、rank(A) = number of pivot columns of A = dimension of C(A).
2、dimension of N(A) = number of free variables = n − r
The four fundamental subspaces
在这个小节中,我来总结一下4个子空间都是什么,以及它们的 basis 和 dimension.
下面我用一个 m×n 的矩阵 A 来说明这4个子空间。前言: 通过一系列消元的过程,我们可以把矩阵 A 转化成 reduced row echelon form R,然后通过 R 可以发现矩阵 A 中的向量的独立性。在消元的过程中,对于 A 的行向量来说,只是进行一些 linear combinations,比如你用第2行减掉2倍的第1行等,因此 A 和 R 的 Row space 的 basis 是一致的。而对于 矩阵 A 的列向量来说,可就不是这样的了,因此当你通过 R 确定 pivots 列以后,然后从矩阵 A 中拿出这些列才是 Column space 的 basis. Row and column spaces 中有找 basis 的例子,你直接看一个例子马上就能明白了。
1、Column space,C(A).
它包含所有矩阵 A 的 columns 的 linear combinations. 很明显,包含 pivots 的列构成 column space 的 basis. 它的 dimension 为 rank r.
2、Nullspace,N(A)
它包含所有使 Ax=0 的解。想要找到 nullspace,需要找到相应的 special solutions,然后把它们进行 linear combinations. 而 special solutions 与 free variables 相对应。你可以回想一下教授找 special solutions 的过程,即把其中的一个 free variables 设为1,其它的设为0,得到一个 special solution,依此类推…… 因此有多少个 free variables,就有多少个 special solutions. 因此 Nullspace 的 dimension 为 n-r
3、Row space,C( AT )
它包含所有矩阵 A 的 rows 的 linear combinations. 关于它的 basis 上面黑体字已经说明了,即 R 中的包含 pivots 的行。因此,Row space 的 dimension 也为 rank r
4、Left nullspace,N( AT )
它就是 AT 的 nullspace. 它的 dimension 为 m-r. 这是因此 AT 变成了 n×m 的矩阵,而 rank 还是 r. 但是它的 basis 如何求呢?因为我们想求 AT y=0 的解,转换一下我们可以写成 AT y= yTATT = yTA =0,看到这个式子估计你也就明白为什么叫做 Left nullspace 了。那么如何求出 Left nullspace 的 special solutions 呢?只 track R 是不够的,我们还需要 track 消元矩阵 E,如下图所示。你会发现 E 中只有最底下的一行使矩阵 A 得到了0. 因此只有这一行构成了 Left nullspace 的 basis.
Orthogonal Vectors and Subspaces
在多变量微积分中,我们已经学习了2个 orthogonal 向量,它们的 dot product 为零。如有2个 orthogonal 向量 v 和 w,那么 vTw=0 . 知道了什么是 orthogonal vectors,下面就是 orthogonal subspaces 的定义:
Subspace S is orthogonal to subspace T means: every vector in S is orthogonal
to every vector in T
下图中有2个 subspace,即2个平面 V 和 W,这个2个 subspace 就不是 orthogonal,虽然2个平面是垂直的,但是你会看到它们之间有个相交的线,而这条直线中的向量即属于 V 又属于 W,它们平行却不垂直,因此 V 和 W 不是 orthogonal 的。因此一个人和你说有1个向量在2个 orthogonal 的 subspace 中,那么这个向量一定是零向量,因为只有它才 perpendicular 它本身,non-zero 向量是不可能做到这一点的。
在上面的小节中,我已经介绍了4个最基本的 subspace,以及它们的 basis 和 dimension. 那么接下来我来介绍一下这4个 subspace 之间的正交关系。其实下图中已经完整地描述了它们之间的关系。
这里我只解释一下为什么 Nullspace is perpendicular to row space? 实际上只要根据 Ax=0 就能得出这样的结论了。由于 Ax=0,那么矩阵的每个行向量乖以 x 都会等于0,如下图所示。但是你可能会想,这几个向量之间的乘积为0,子空间就 orthogonal 了吗!答案是肯定的。不信的话你可以把求出的 special solutions 进行 linear combinations,从而随意得到一个 Nullspace 中的向量,然后你再把矩阵的行进行 linear combinations 一下,从而得到 row space 中的任意一个向量,最后你会发现,它们的乘积依然为0,因此 Nullspace 中的任意一个向量与 row space 中的任意一个向量都垂直,所以这2个子空间是 orthogonal. 同样的道理,column space 和 left nullspace 也是 orthogonal.
更进一步地讲,Nullspace 与 row space 是 orthogonal 的,而且它们还是 orthogonal complements in Rn . 这里我需要更进一步地解释一下 complement 是什么意思?关于它的定义我引用了 What is the difference between orthogonal subspaces and orthogonal complements? 中的一部分内容。因此从下面的定义可以得出:Nullspace 与 row space 的交集只有零向量,并且它们可以 span 整个 Rn .
Given a vector space V , the vector subspaces X,Y≤V are complementary iff (a) X and
Y are transverse, that is, X∩Y={0} and (b) X andY span V
因此,比如我们说 R3 中有2个子空间 orthogonal complements,它们不仅仅是 orthogonal,而且 span 它们可以构成整个 R3 . 你也可以看一下 Orthogonal Vectors and Subspaces 中的 Recitation video,那么这个 video 中的第2个问题可以解释为:row space S 和 nullsapce S⊥ 它们是 orthogonal complements,因此它们的 span 会构成整个 R4 ,即求 nullsapce 中的2个 special solutions 和给定的2个行向量,总共4个向量 span 会构成整个 R4 ,因此这4个向量一定是独立的。
Projections onto Subspaces
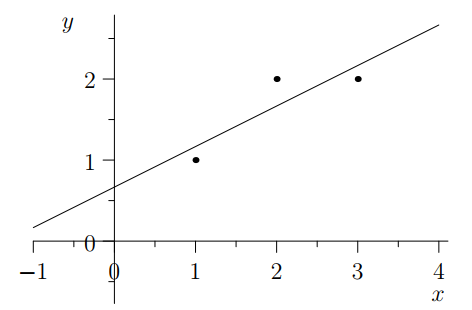
在现实生活中的应用中会存在 noise,这会导致方程的数量大于未知数的数量,即 m > n,从而致使 Ax=b 无解。比如下面的 least squares 问题,这里有2个未知数 x 和 y,却有3个方程, y=ax+b(a+b=1, 2a+b=2, 3a+b=2),把这3个方程写成矩阵的形式就是 Ax=b.
由于 noise 的存在,因此不可能有一个完美的解,但是我们依然想要找到一个 best possible solution。对于上面的例子来说,虽然找不到一条通过3个点的线,但是我们想尽可能的找出一条使其误差最小的线。用矩阵的形式来说,由于实际应用存在 noise,这会导致 Ax=b 无解,即向量 b 不在矩阵 A 的 column space 上,为了找到一个 best possible solution,我们需要把向量 b 映射到 column space 上,从而得到一个 best possible solution, 那么现在主要的问题就是如何映射呢?
在总结如何映射之前,给出一个定理:
When A has independent columns, ATA is square, symmetric, and invertible.
Proof: 假设 A 是一个 m×n 的矩阵,那么 ATA 就是一个 n×n 的方阵; 因为 (ATA)T=AT(AT)T=ATA ,所以它是 symmetric 的; 一个 invertible 的矩阵就是每个 pivot 不能为0的方阵,即这种矩阵的 nullspace 只有 zero vector。When the columns of A are linearly independent, its nullspace contains only the zero vector,又由于 ATA 和 A 有着同样的 nullspace,因此 ATA 是 invertible 的矩阵。
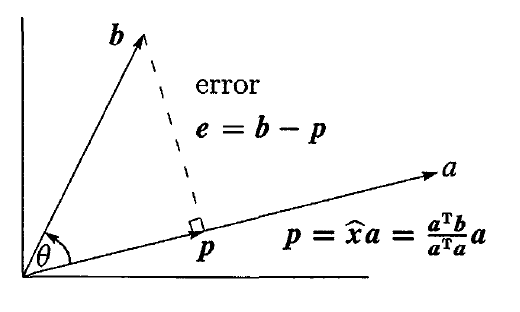
下面2幅图是关于 projection 的 精髓所在,对于映射到一条直线上的例子,通过向量 e 与 a 之间的垂直关系,可以求出 x^ ,如果你把它的点积形式简化一下,实际上就是向量 b 乖上 它与 向量 a 之间夹角的余弦,但是 using the transpose is better, because it applies also to matrices. 实际上, x^ 就是映射 p 的长度。
那么是谁作用向量 b 得到 p 的呢?答案是 projection matrix!如果你把上面的公式调整一下,可得到下图的形式,即得到了projection matrix P. 在这个映射到直线的例子中,a 是一个向量,因此 aTa 是一个数,而 aaT 是一个 m×m 和矩阵,所以 P 就是一个 m×m 的矩阵。Pb=p,由于映射之后的结果 p 始终在一条直线上,因此 P 的 column space 就是 one-dimensional subspace,它的 rank=1
关于 projection matrix 有2个性质:1) P2=P ,这是因为 projecting a second time doesn’t change anything,it still projects onto the same line for the above example. 2) P is symmetric,即 PT=P ,不难发现,上图中的 P 的分母是个数,分子为矩阵 aaT , (aaT)T=(aT)TaT=aaT
In R3 , how do we project a vector b onto the closest point p in a plane?实际道理和上面都是一样的。看一下 Lecture 15 的 18:50-31:40,非常简单,一下就可以明白了,或者你也可以参考 Projection in higher dimensions 这一小节。这里我只总结一下得到的结果,你会得到一个非常重要的等式:
实际上,它和上面映射到直线上的那个例子一样,只不过先前的向量 a,现在变成了矩阵 A; 先前的 aTa 仅仅是一个数,现在的 ATA 是一个矩阵,因此不能像先前那样,写成除法的形式,这回应该是用逆矩阵的形式得到: x^=(ATA)−1ATb ,求出了 x^ ,现在可以得到 projection matrix 了,如下图所示:
注意:上面的式子是不能简化的,除非 A 是方阵,否则不能说: (ATA)−1=A−1(AT)−1 ,如果 A 是一个 square, invertible matrix,证明它的 column space 是整个空间,包含b,因此b的映射就是它自己,因此P应该为I,如果你简化上面的式子以后,P确实是 I,这证明我们得到的结论是一致的。上面我提到的关于 P 的2个性质,在这里依然成立。
话说回来,对于上面的 least squares 问题,Ax=b 没有解的,现在我们可以对 ATAx^=ATb 来求解。通过上面的解释,相信大家已经知道这个公式背后的逻辑了,即把 b 映射到 A 的 column space 上,从而可以求出解了。Projection matrices and least squares 这篇文章中有一个完整的例子解决 least squares 问题。
Orthogonal Matrices and Gram-Schmidt
至此,我们已经学习了很多重要的矩阵:triangular, diagonal, permutation, symmetric, reduced row echelon, and projection matrices. 在这个小节中,将会学习到 orthonormal matrix. 从名字可以看出来,这个矩阵的 columns 是相互垂直的,并且每个 columns 的长度是1.
那么我们为什么需要这样的矩阵呢?它有什么好处吗?答案是好处大大的。在上个小节中,我们已经得出了 projection matrix P=A(ATA)−1AT ,这回把具有更多性质的 orthonormal matrix Q 代入原式,可以得到 P=QQT ,实际上,根据 orthonormal matrix 的定义不难得出, QTQ=I . 因此,orthonormal matrix 的出现大大简化了 projection matrix 的表达式。当 Q 为方阵时, P=QQT=I ,这是因为 Q 的列 span 整个空间(Q 的列都是 independent 的),因此映射的结果一定是 b 本身,即 b 在 column space 中,所以 P=I
实际上我们通常关心的是如何求出 Ax=b 的解,如果解不存在,我们想找出 best possible solution,通过将 b 映射到 A 的 column space 上,从而得到解。刚刚我们知道了 orthonormal matrix 可以简化整个过程,从而更加容易地求出解。因此,我们现在的目标就是如何把矩阵 A 转换成 Q,并且它们最后会 span 同一个空间。用 Gram-Schmidt 可以实现这个目标。
Gram-Schmidt orthogonalization: given a non-orthonormal basis a₁,a₂,…, we can convert it to an orthonormal basis that spans the same space. All we do is to take each vector and subtract the projections onto the previous vectors to make them orthogonal, and divide by their lengths to normalize them. 具体步骤参考下图,更加详细的解释请看 lecture 17 的后半部分。
Gram-Schmidt 过程将 A 转换成了 Q,那么一定有一个矩阵关联这2个矩阵(类似于文章上面介绍的消元矩阵,),这个矩阵就是 R=QTA ,这是因为 QTQ=I ,因此得到下图中的矩阵 R. 那么为什么 R 是一个 upper triangular 的矩阵呢?其实也很简单,首先参考一下 Gilbert Strang 教授在 lecture 17 中介绍的 Gram-Schmidt 过程(26:30–34:20),用下图中的例子解释就是 q1 就是 a1 方向上的单位向量(这是因为选择的第一个向量保持在原方向上不变),按照 Gram-Schmidt 过程,然后通过映射的手段,即上图公式中的第2步,可以根据向量 a2 得到一个垂直于 a1 (即垂直于 q1 ),的向量,把这个向量 normalization 以后就得到了 q2 ,因此 q2 也是垂直于 a1 的,以此类推,后续得到的 q2,q3,… 都会 perpendicular 先前的向量。因此,对于下图中的例子来说, aT1q2=0 ,所以是 upper triangular 的矩阵。
这篇关于MIT 18.06 线性代数总结(Part I)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!