【坐在马桶上看算法】算法9：开启“树”之旅

我们先来看一个例子。

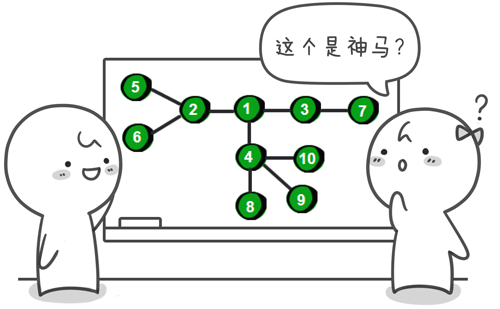
       这是什么？是一个图？不对，确切的说这是一棵树。这哪里像树呢？不要着急我们来变换一下。

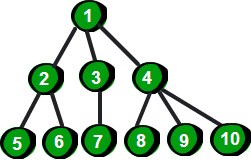
       是不是很像一棵倒挂的树，也就是说它是根朝上，而叶子朝下的。不像？哈哈，看完下面这幅图你就会觉得像啦。

       你可能会问：树和图有什么区别？这个称之为树的东西貌似和无向图差不多嘛。不要着急，继续往下看。树其实就是不包含回路的连通无向图。你可能还是无法理解这其中的差异，举个例子，如下。

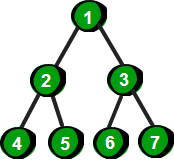
       上面这个例子中左边的是一棵树，而右边的是一个图。因为左边的没有回路，而右边的存在1->2->5->3->1这样的回路。
       1、正是因为树有着“不包含回路”这个特点，所以树就被赋予了很多特性。
       2、一棵树中的任意两个结点有且仅有唯一的一条路径连通。
       3、一棵树如果有n个结点，那么它一定恰好有n-1条边。

       在一棵树中加一条边将会构成一个回路。树这个特殊的数据结构在哪里会用到呢？比如足球世界杯的晋级图，家族的族谱图、公司的组织结构图、书的目录、我们 用的操作系统Windows、Liunx或者Mac中的“目录（文件夹）”都是一棵树。下面就是“啊哈C”这个软件的目录结构。

假如现在正处于libexec文件夹下，需要到gdiplus文件夹下。你必须先“向上”回到上层文件夹core，再进入include文件夹，最后才能进入gdiplus文件夹。因为一棵树中的任意两个结点（这里就是文件夹）有且仅有唯一的一条路径连通。

       为了之后讲解的方便，我们这里对树进行一些定义。
       首先，树是指任意两个结点间有且只有一条路径的无向图。 或者说，只要是没有回路的连通无向图就是树。

       喜欢思考的同学可能会发现同一棵树可以有多种形态，比如下面这个两棵树。

       为了确定一棵树的形态，在一棵树中可以指定一个特殊的结点――根。我们在对一棵树进行讨论的时候，将树中的每个点称为结点，有的书中也称为节点。有一个 根的树叫做有根树（哎，这不是废话嘛）。比如上方左边这棵树的树根是1号结点，右边这棵树的树根是3号结点。

       根又叫做根结点，一棵树有且只有一个根结点。根结点有时候也称为祖先。既然有祖先，理所当然就有父亲和儿子。比如上图右边这棵树中3号结点是1、6和7 号结点的父亲，1、6和7号结点是3号结点的儿子。同时1号结点又是2号结点的父亲，2号结点是1号结点的儿子，2号结点与4、5号结点关系也显而易见 了。

       父亲结点简称为父结点，儿子结点简称为子结点。2号结点既是父结点也是子结点，它是1号结点的子结点，同时也是4和5号结点的父结点。另外如果一个结点 没有子结点（即没有儿子）那么这个结点称为叶结点，例如4、5、6和7号结点都是叶结点。没有父结点（即没有父亲）的结点称为根结点（祖先）。如果一个结 点既不是根结点也不是叶结点则称为内部结点。最后每个结点还有深度，比如5号结点的深度是4。哎，终于�嗦完了，写的我汗都流出来了，没有理解的请看下面 这幅插图吧。

       说了这么多你可能都没有感受到树究竟有什么好处。不要着急，请看下回――二叉树。

       欢迎转载，码字不容易啊，转载麻烦注明出处

     【啊哈！算法】算法9：开启“树”之旅  http://ahalei.blog.51cto.com/4767671/1403823