本文主要是介绍python实现光线追迹(上),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 几何抽象
- 光线
- 线段与圆弧
传统的高斯光学是建立在傍轴近似基础之上的理想成像理论,这种处理以物像关系为核心,通过基点对光路的成像特性进行描述。然而,傍轴近似在一定程度上牺牲了精确性,从而使得需要一套像差理论作为补充。
得益于计算机的计算的能力,通过追踪具有代表性的光线的传播轨迹,可以更加精确地描述光学系统的性能,光线追迹方法也因此大展其能,诸如Zemax、tracepro等软件便都提供了相应的功能。
而建立在折射定律基础之上的光线追迹方法,对数学功底要求较低,所以比较适合作为python初学者的入门项目。在接下来的这一章,希望通过对光线追迹的实现,掌握python中的列表、元组、字典、集合等数据类型的基本概念,并且对面向对象与函数式编程有一个基本的了解。
几何抽象
光线
光线追迹描述的是光线与光学元件接触之后的行为变化,因此首先需要对光线与光学元件进行刻划。由于我们希望最终建立一个二维的光路系统,光线既可能水平,也可能竖直,因此通过 a x + b y + c = 0 ax+by+c=0 ax+by+c=0来表示一条光线。即只需$a b c $这三个数字,便可以确定二维空间中的一条直线。
在python中,可以通过序列-list来表示一组数据,在list中,每个元素都分配一个数字作为索引,可以通过索引来提取或改变list中的值。需要注意的是,和诸多编程语言类似,python中的索引也是从0开始的。所以我们可以在python中新建一个变量来表示一条过原点斜率为1的直线:
>>> abc=[1,-1,0] #在python中,list用方括号表示
>>> type(abc) #type函数可以返回数据类型
<class 'list'>
>>> abc[0] #在python中,用方括号进行索引
1
>>> abc[1] = 5 #list中的值可以更改
>>> abc[-1] #在python中,索引-1往往表示倒数第一个值
0
>>> abc #修改后的abc
[1, 5, 0]
当然,光线实质上是一种有源的射线,所以需要对直线方程 a x + b y + c = 0 ax+by+c=0 ax+by+c=0进行符号约定,进而明确其方向性。
考虑到[a,b,c]与[-a,-b,-c]可以表示同一条直线,所以我们可以通过 a a a和 b b b的正负号来表明其方向。通过射线终点所在象限对[a,b]的正负号进行限定,可以得到几组不同的符号约定,在此我们选取如下约定:
| a | b | 象限 | 举例 | list |
|---|---|---|---|---|
| + | - | 1 | x − y + 1 = 0 x-y+1=0 x−y+1=0 | [1,-1,1] |
| + | + | 2 | x + y + 1 = 0 x+y+1=0 x+y+1=0 | [1,1,1] |
| - | + | 3 | − x + y − 1 = 0 -x+y-1=0 −x+y−1=0 | [-1,1,-1] |
| - | - | 4 | − x − y − 1 = 0 -x-y-1=0 −x−y−1=0 | [-1,-1,-1] |
可以看到第一、三条射线的方程表示同一条直线,但由于引入符号约定,所以我们可以区分其方向上的差别,从而可以判断这条光线是否会与某一光学元件相交。
如果希望绘制出一条光线,可以调用python的UI库wxpython,为了不影响内容的连贯性,这种方法会在后面统一讲解。
除了这里所推荐的直线的abc表示法,我们还可以通过始点与角度来对光线进行表示,我们同样可以使用三个参数[x0,y0,theta]。但是在进行计算的时候,需要先将其转换成为[a,b,c]的表示方法,因此需要定义转换函数,即通过初始点和角度生成射线的函数,考虑到此前的符号约定,其转换公式为
l : s i n θ ⋅ x − c o s θ ⋅ y − ( s i n θ ⋅ x 0 − c o s θ ⋅ y 0 ) = 0 l:sin\theta\cdot x - cos\theta\cdot y -(sin\theta\cdot x_0 - cos\theta\cdot y_0)=0 l:sinθ⋅x−cosθ⋅y−(sinθ⋅x0−cosθ⋅y0)=0
即
[ x 0 , y 0 , θ ] → [ s i n θ , − c o s θ , − ( s i n θ ⋅ x 0 − c o s θ ⋅ y 0 ) ] [x_0,y_0,\theta]\to [sin\theta ,-cos\theta ,-(sin\theta\cdot x_0 - cos\theta\cdot y_0)] [x0,y0,θ]→[sinθ,−cosθ,−(sinθ⋅x0−cosθ⋅y0)]
需要注意的一点是,这里需要调用numpy包来使用三角函数。
import numpy as np
x0,y0,theta = [0,0,np.pi/4] #np.pi即圆周率
abc = [np.sin(theta), #在python中,括号内换行可以不用标记-np.cos(theta),-(np.sin(theta)*x0-np.cos(theta)*y0)]
由于这个方法可能会被经常使用,所以可以封装成函数,在python中,通过关键字def进行函数的定义。对于参数个数和返回值的个数以及数据类型几乎没有限制。故可以写为
import numpy as np
def getABC(x0,y0,theta): #函数定义格式为 def 函数名(传入参数):a = np.sin(theta) #函数下方需要进行缩进b = -np.cos(theta)c = -(np.sin(theta)*x0-np.cos(theta)*y0)
return a,b,c #在python中,通过return返回abc参数
也可以写为
import numpy as np
def getABC(x0,y0,theta):return [np.sin(theta), #在括号内可以直接换行-np.cos(theta),-(np.sin(theta)*x0-np.cos(theta)*y0)]
在命令行中调用
>>> import test
>>> import numpy as np
>>> test.getABC(0,0,-np.pi/4)
[-0.7071067811865476, -0.7071067811865476, 0.0]
线段与圆弧
在光学系统中,最常见的光学器件便是平面镜和透镜,则其在入射光线子午面上的投影可拆解为线段和圆弧。
对于线段,可以非常直观地通过两个点进行表示。在python中,除了列表之外,可以用元组(tuple)来表示序列,不同之处在于元组的元素不能修改。在此,用饱含两个元素的元组来表示一个点,将两个点组成列表来表示线段:
>>> a = (0,0) #在python中,元组用小括号表示
>>> b = (1,1)
>>> seg = [a,b] #列表中的元素可以有不同的类型
>>> seg
[(0, 0), (1, 1)]
>>>
圆可以通过圆心与半径来表示,简洁而利于计算。圆弧则可以通过圆与角度来表示。但是作为光学元件的组成部分,为了便于后面的处理,其表现形式最好与线段相似,即通过三点即A、B、C来确认一段圆弧。
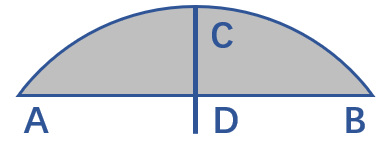
但是具体计算的过程中往往需要将圆弧转换成圆的表达形式进行操作,所以定义函数arc2cir来实现这个功能。由于其数学过程过于简单,故只对一些命令进行说明,其中np.lialg为numpy的线性代数包,np.linalg.norm为求范数,np.linalg.norm(a-b)相当于求a、b两点之间的距离。
def arc2cir(arc):arc = np.array(arc) #list不能进行数组运算,需要转成np.array的形式dCD = np.linalg.norm(1/2*(arc[0]+arc[1])-arc[2]) #CD长度dBC2 = np.sum(np.square(arc[1]-arc[2])) #BC**2radius = 0.5*dBC2/dCD #圆半径theta = (arc[2]-1/2*(arc[0]+arc[1]))/dCD #三角函数值zero = arc[2]-radius*thetareturn list(zero)+[radius] #列表相加为其内部元素的合并
需要注意的是,在python中,list、tuple都不支持整体上的数学计算,这很容易理解,因为二者中存储的不一定是数字,而可能是其他的什么东西。格式不同,自然无法计算。因此在考虑计算之前,需要将二者转换成numpy.array这种数组格式。
列表、元组、数组之间的转换非常简单而直观。
import numpy as np
>>> lis = [1,2,3]
>>> tup = tuple(lis)
>>> arr = np.array(tup)
>>> arr
array([1, 2, 3])
>>> lis
[1, 2, 3]
>>> tup
(1, 2, 3)
这篇关于python实现光线追迹(上)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








