Sergey's problem CF1019C

这真是有趣的题目啊（不是吗？）

题目描述

今天是T一岁的生日（真不容易），当她刚出生一秒的时候，她的太……太爷爷L给了她一颗钻石（有一个编号），
当她出生2秒时，L高兴她生来畸形，却能活过2秒，给了她一个钻石项链（均有编号），在她出生3秒时，
xay兴奋过度，留给她一根纯钻石的绳子……
当她出生4秒时，L实在太开心了，死了，当他知道自己的死期时，特意为写了一张字条给她母亲（打算在T周岁时给他）
Today，T的母亲温柔和蔼地叫醒了她，T撑着她那书包一样大的脑袋，睁开了她那漂亮的眼睛，
晶莹，剔透，无与伦比，这真是这个世界上最漂亮的眼睛，可惜只有用探测隧道显微镜才能看到……
她的首富爸爸希望她能做一个好孩子，志不能残，要好好学习信奥，于是给了她……一颗有根树？？（这比L的礼物差远了，不是吗》），
但是，T不想当农民（显然他理解错了），她要了一个玩具（好奇怪的要求）作为礼物，首富爸爸满足了她

由于T非常喜欢嬉戏，特别是搓炉石传说（没有什么关系），她的玩具是一个有向图Q的拼装，她不是很理解这个怎么玩~于是就有了自己的想法，她想找到一组顶点，始这组点没有两个定点$x,y\in Q$，且对于任何一个不属于S集合的一个点中，$x$到达$y$的距离能<=2，且x和y在原图中没有边相连;

T很小，但她自己只会胡乱搭建一个有向图（首富买的就是不一样，买的玩具有n个点，m个边（$n，m<=10^6）$），找到这先点集的点就交给你了~

题目保证有解~~~~

输入格式

第一行，两个正整数，$n$，$m$,表示这个题有$n$个点，$m$条边

剩下有$m$行

每行有两个整数$x$,$y$。表示x到y有一条有向连边

输出格式

第一行，一个整数，表示这个点集有 $S$大小

剩下$S$行

分别是这些点的编号（从小到大排序，中间有空格）

样例数据

input1
5 4
1 2
2 3
2 4
2 5
output1
4
1 3 4 5

(良心出题人

input2
3 3
1 2
2 3
3 1
output2
1
3

很不错，毕竟这是我自己翻译，比较皮~~

大意网上有一个翻译很淳朴，很清楚

题目大意

给你一个n个点，m条边的 有向图

要求选出一个点集S，满足S中的任意两点间没有边相连
且对于任何一个不属于S的点y
必然存在S中的某个点x满足

网上有一个题解写的非常详细，但很无奈，写的自我感觉并 不是很让初学者能看懂 ~
送上一个必定让人看懂 的（看不懂，私信）

先看看样例解析：

对于第一个样例：
顶点1,3,4,5未连接。 顶点2可以通过一个边缘从顶点1到达。

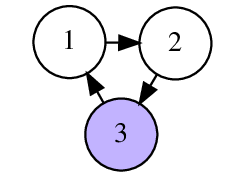
对于第二个样例
3可以在一次移动中到达顶点1，在两次移动中到达顶点2。

来个简单的题解

先一个图，先扫一遍 选出一个没有被删掉的点（这个删掉不是真的要删掉）
然后把它所连上的那些边（是可能有多个的）删除掉 并把这个点放入集合S中 也删除它 一直做下去，直到这一个图没有点了~
然后这个图，还原再按编号倒序遍历集合中的点，如果它指向了一个编号较小的，且在集合中的点，那么把那个点从集合中删除。
画个图举个例子：
8 7
1 2
2 3
2 4
3 4
3 5
4 5
4 6
对于这个图
我们先找到第一个点1删除其连边1 2 选择3，删除4 5；选择6，不能删除，7,8同理； 这样就把最短路1 的情况处理完了。
集合里的是1,3,6,7,8
再按编号倒序遍历集合中的点，如果它指向了一个编号较小的，且在集合中的点，那么把那个点从集合中删除，显然这个数据不太好，没有需要删除的 。
所以说个的答案就是，1 3 6 7 8（其实就是左边扫一遍，右边扫一遍）

但是不要以为可以不用右扫哦，你要想到，样例2良心的把需要右扫一遍的，不然会是1,3

显然应该是要3的，1 是被3用连上了的，所以特别要注意环这种情况

证明来源于那位大神：
因为两个属于答案集合点不能一步到达。
满足x∈V,x∉v 的节点 x，在左边扫的时候就被删掉了~
满足 x∈v,x∉S（答案集合）的节点 x，会在右边扫描的时候删除掉。显然有一个能一步到达 x 的节点 y 在集合 v 中。
如果 y∉S，有一步到 y 的节点的话， x 可以两步到达。y∈S ，x 可以由 y 一步到达。//证明其实可能不正确，但是：
最重要的关键证明：根据cf的AC可以判断，是对的（ 不然其它白扯 ~

贴上我的代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1000005;
int n,m,cnt=0,len;
int vis[N],ans[N],last[N];
struct ss
{int to,next;
}e[N];
void insert(int x,int y)
{e[++len].next=last[x],e[len].to=y,last[x]=len;
}
int main()
{freopen("T.in","r",stdin);freopen("T.out","w",stdout); int i,j;scanf("%d%d",&n,&m);for(i=0;++i<=m;){int x,y;scanf("%d%d",&x,&y);insert(x,y); }for(i=0;++i<=n;)//左边扫 if(!vis[i]){vis[i]=-2;for(j=last[i];j;j=e[j].next)vis[e[j].to]=min(vis[e[j].to],-1);}for(i=n;i>=1;--i)//右边扫 if(vis[i]==-2){ans[++cnt]=i;for(j=last[i];j;j=e[j].next)vis[e[j].to]=-1;}printf("%d\n",cnt);for(i=cnt;i>=2;--i)printf("%d ",ans[i]);printf("%d",ans[1]);return 0;
}

谢谢观赏哦~