本文主要是介绍请要相信我，30分钟让你掌握AVL树（平衡二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
请要相信我，30分钟让你掌握AVL树（平衡二叉树）
请要相信我，30分钟让你掌握AVL树（平衡二叉树）
前言：本文不适合 给一组数据15分钟就能实现AVL的插入和删除操作的大牛（也请大牛不要打击小菜）
本文适合，对avl还不了解，还没有亲自实现avl的插入和删除操作的同学
ps，你在嘲笑楼主的题目时，你已证明了自己正在嘲笑自己的智商。我们要善于征服陌生的事物。你如果有半个小时时间就心无杂念的开始吧，建议那些读10分钟文章就心燥还是关闭浏览器吧。
文章结构：
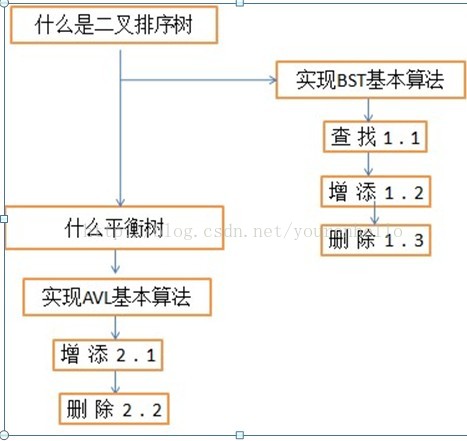
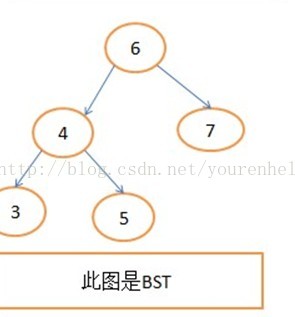
什么是二叉排序树（bst）
typedef struct _BitNode
{int data;struct _BitNode *lchild,*rchild;
}BitNode,*BiTree;
// 3:如果返回真把目标到元素的指针指向n，返回假，就把pre复制给n）（参数如果不明白，先不要细究，往下看吧）
bool SearchBST(BiTree T,int key,BiTree pre,BiTree&n);
bool SearchBST(BiTree T,int key,BiTree pre,BiTree&n){if(!T){n=pre; //如果此数为空树，那我们就把前一个元素指针pre（此时为NULL）复制给n，注意树为空时，n才为NULL。return false; //返回假没有找到}else if(key==T->data){n=T; //找到了就把目标元素指针给nreturn true;}if(key<T->data)SearchBST(T->lchild,key,T,n) ;//去找他的左子树根比else{SearchBST(T->rchild,key,T,n);//去找他的右子树根比。}}bool InsetBST(BiTree &T,int k){BitNode* p;if(!SearchBST(T,k,NULL,p)){ BitNode * temp=new BitNode;temp->data=k;temp->lchild=temp->rchild=NULL;if(!p) //只有树为空时，此时的p才为NULL。看到这里应该明白SearchBST(T,k,pre,p)这些参数的意义了吧{T=temp; }else{if(k<p->data) //如果不为空树，加入的key值就和p相比较，小于就是他的左孩子，否子为右孩子p->lchild=temp;else{p->rchild=temp;}}return 0;}else {return false;}}删除总共有3种情况，1只有左子树；2，只有右子树；3，左右子树都有。
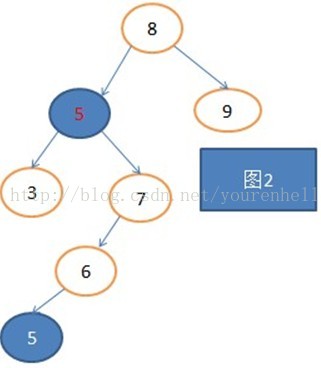
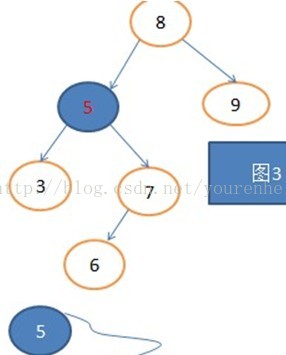
bool DeleElement(BiTree&T,int key){if(!T){return 0; //树是空树的话就返回假}if(T->data==key){BitNode*s,*p;if(T->rchild==NULL) //只有右子树，情况2{ s=T;T=T->lchild;free(s);}else if(T->lchild==NULL){s=T; //只有左子树，情况1T=T->rchild;free(s);}else{ //情况3，左右子树都有p=T;s=T->rchild;while (s->lchild){p=s; //找到所要删除节点的后继，那就是他的右孩子的s=s->lchild;}T->data=s->data; //用删除节点的后继替换所删除的节点if(p!=T) {p->lchild=NULL; //所删除的节点的右孩子不是叶结点}else p->rchild=NULL; //所删除的节点的右孩子是叶节点free(s);}return 1;}else if(key<T->data)DeleElement(T->lchild,key); //去和他的左子树根去比较else DeleElement(T->rchild,key); //去和他的右子树根去比较}//中序遍历并输出元素void InorderReverse(BiTree T){if(T){InorderReverse(T->lchild);cout<<T->data<<endl;InorderReverse(T->rchild);}}int main()
{BiTree tree=NULL;int a[]={60,86,50,40,35,74,51,100,37,90};for(int i=0;i<10;i++)InsetBST(tree,a[i]);InorderReverse(tree);cout<<" "<<endl<<endl;DeleElement(tree,62);InorderReverse(tree);return 0;
}到这为止二叉排序树已经搞定了，如果你自己也实现了上述功能，那证明你有很强的好奇心并且很有天赋（因为楼主搞了好几天才明白，你十几分就搞定了，那不是最好的证明吗？ps：楼主是那种很迟钝但很有毅力），有了前面的基础，AVL就是手到擒来，不要灰心哦，鼓足劲就继续征程吧。如果没有理解，先暂停会，避免浪费不必要的时间，就不要往下看了，建议反复认真看几遍，如果还不理解，可能这篇文章不适合你，建议参考其它文章。
平衡二叉树定义(AVL)：它或者是一颗空树，或者具有以下性质的二叉树：它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1，且它的左子树和右子树都是一颗平衡二叉树。
平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1,这里我们定义:
#define EH 0,#define LH 1,#define RH -1.依次为等高，左高，右高。
typedef struct _BitNode
{
int data;
int bf;//平衡因子
struct _BitNode *lchild,*rchild;
}BitNode,*BiTree;
我们都知道，平衡二叉树是在二叉排序树(BST)上引入的(这一点很重要哦，下图为例），就是为了解决二叉排序树的不平衡性导致时间复杂度大大下降，那么AVL就保持住了(BST)的最好时间复杂度O(logn)，所以每次的插入和删除都要确保二叉树的平衡，那么怎么保持平衡呢？如果还不理解看看下面的图吧。
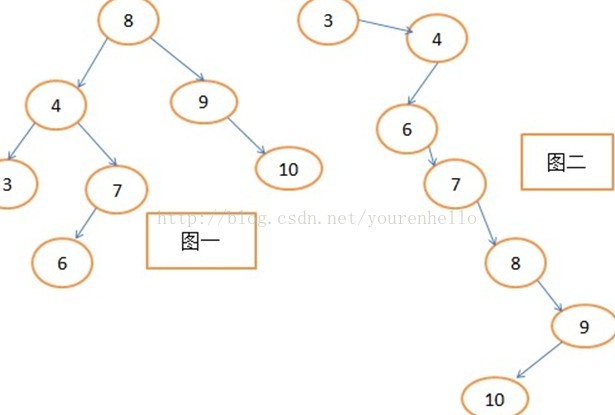
， 平衡因子为0.
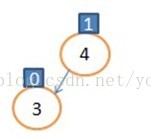，4的平衡因子因为4的左子树增长了，1-0=1，
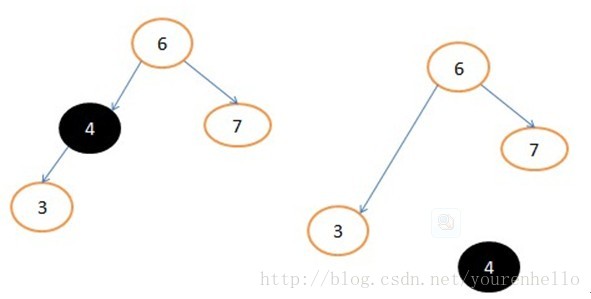
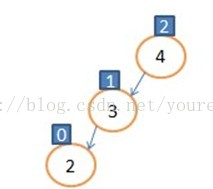，显然4的平衡因子大于1了，为了保持平衡那我们就这样做：让4节点的左孩子指向3的右子树（此时为NULL），让3的右孩子指向4，让树根指向3，如图 
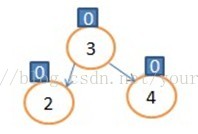，这种操作我们规定为右旋操作，此图是以4为根进行旋转。 代码如下
void R_Rotate(BiTree&T)
{BiTree p; //p=T->lchild; //假如此时T指向4，则p指向3；T->lchild=p->rchild; //把3的右子树挂接到4的左子树上（此例子3右子树为空）p->rchild=T; //让3的右孩子指向4.T=p; //根指向节点3
}
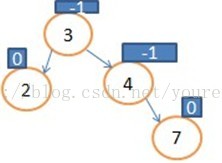
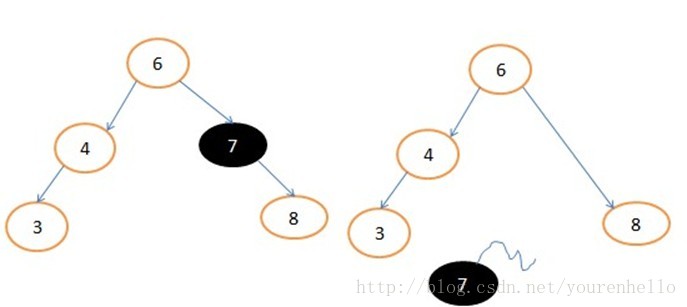
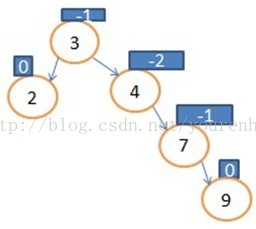显然节点4不平衡了。那我们就把4的右孩子7的左子树（此时为NULL），让7的左孩子指向4，让3的右孩子指向7，如图： 
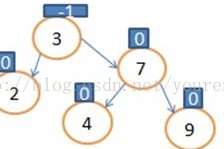，我们规定此操作为左旋操作，此图是以4为根进行旋转，代码如下：
void L_Rotate(BiTree&T)
{BiTree p;p=T->rchild; //假如此时T指向4，则p指向7.T->rchild=p->lchild; //让7的左子树挂接到4的右子树上p->lchild=T; //让7的左孩子指向4T=p; //树根指向7
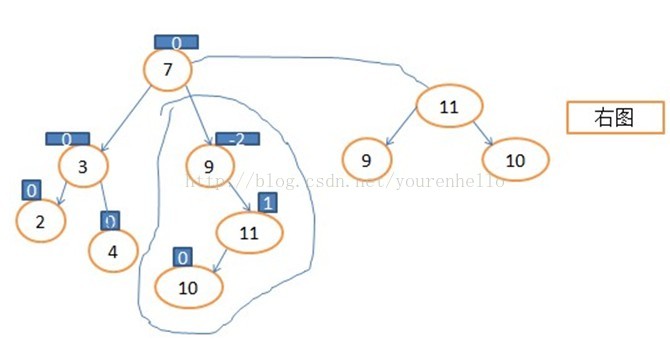
} 6.我们插入11，如图：
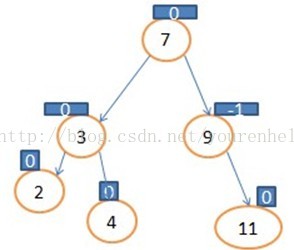
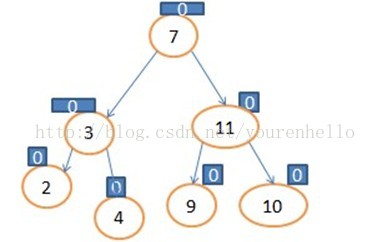
7.我们插入10，如图：
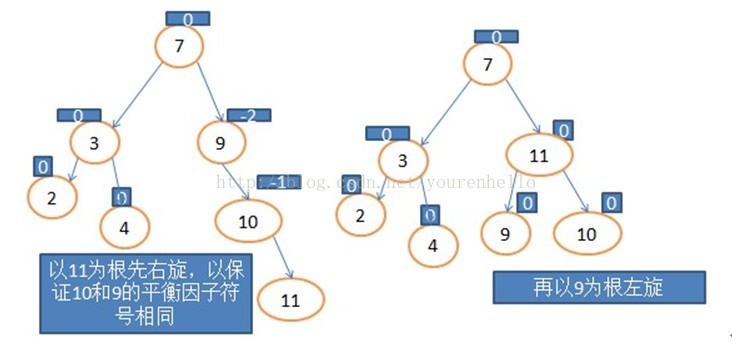
LeftBalance()功能:当左高时需要左平衡时调用；
void RightBalance(BiTree&T)
{BiTree R,rl; //调用此函数时，以T为根的树，右边高于左边，则T->bf=RH。R=T->rchild; //R是T的右孩子switch (R->bf){case RH: //如果 T的右孩子和T他们的平衡因子符号相同时，则直接左旋，这是总结中的第2项T->bf=R->bf=EH; L_Rotate(T);break; case EH:T->bf=RH;R->bf=LH;L_Rotate(T);break;case LH: //如果T的右孩子和T他们的平衡因子符合不同时，需要先以T的右孩子为根进行右旋，再以T为根左旋。//rl为T的右孩子的左孩子rl=R->lchild; //2次旋转后，T的右孩子的左孩子为新的根 。注意：rl的右子树挂接到R的左子树上，rl的左子树挂接到T的右子树上switch (rl->bf) //这个switch 是操作T和T的右孩子进行旋转后的平衡因子。{case EH:T->bf=R->bf=EH; //这些平衡因子操作，大家可以自己画图操作理解 下面的注解break;2次旋转后，T的右孩子的左孩子为新的根 。//并且rl的右子树挂接到R的左子树上，rl的左子树挂接到T的右子树上，rl为新根case RH:R->bf=EH;T->bf=LH;break;case LH:R->bf=RH;T->bf=EH;break;default:break;}rl->bf=EH; R_Rotate(T->rchild); //先左旋，以T->rchild为根左旋。L_Rotate(T); //右旋，以T为根, 左旋后 T是和rl想等，rl是新根break;}
}
void LeftBalance(BiTree&T)
{BiTree L,lr;L=T->lchild;switch (L->bf){ case EH:L->bf=RH;T->bf=LH;R_Rotate(T);break;case LH:L->bf=T->bf=EH;R_Rotate(T);break;case RH:lr=L->rchild;switch (lr->bf){case EH:L->bf=L->bf=EH;case RH:T->bf=EH;L->bf=LH;break;case LH:L->bf=EH;T->bf=RH;break;default:break;}lr->bf=EH;L_Rotate(T->lchild);R_Rotate(T);break;default:break;}
}bool InsertAVLtree(BiTree&T,int key,bool&taller)
{if(!T) //此树为空{T=new BitNode; //直接作为整棵树的根。T->bf=EH;T->lchild=T->rchild=NULL;T->data=key;taller=true;return true;}else{ if(key==T->data) //已有元素，不用插入了，返回false；{taller=false;return false;}if(key<T->data) //所插元素小于此根的值，就找他的左孩子去比{if(!InsertAVLtree(T->lchild,key,taller)) //所插元素小于此根的值，就找他的左孩子去比 return false;if(taller) //taller为根，则树长高了，并且插入到了此根的左子树上。{switch (T->bf) //此根的平衡因子{case EH: //原先是左右平衡，等高T->bf=LH; //由于插入到左子树上，导致左高=》》LHtaller=true; //继续往上递归break;case LH:LeftBalance(T); //原先LH，由于插入到了左边，这T这个树，不平衡需要左平衡taller=false; //以平衡，设taller为false，往上递归就不用进入此语句了，break;case RH:T->bf=EH; //原先RH，由于插入到左边，导致此T平衡taller=false;break;default:break;}}}else {if(!InsertAVLtree(T->rchild,key,taller))return false;if(taller){switch (T->bf){case EH:T->bf=RH;taller=true;break;case LH:T->bf=EH;taller=false;break;case RH:RightBalance(T);taller=false;break;default:break;}}}}//中序遍历输出
void InOrderReverse(BiTree&T)
{if(T){InOrderReverse(T->lchild);cout<<T->data<<endl;InOrderReverse(T->rchild);}
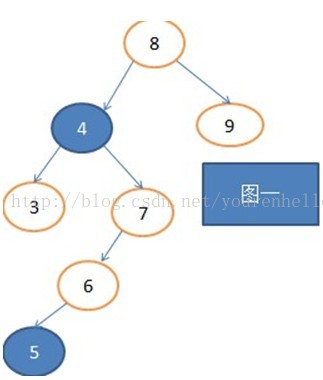
}看到这了，自己出一组数据或按照我刚才用一组数据拼成avl的过程，看代码走一遍，你会有不一样的收货的哦(这其实非常重要)，并插入了成功了，你已经成功99%了，没有想到自己这么厉害吧，我们接下来完成它的删除操作，我们就完美了。如果你有追求完美的目标，那就跟我走吧 2.2AVL的删除操作
下面我会贴出代码，根据代码把上图的元素删除掉吧，你会成功的
为了更好的理解，建议先把插入代码先实现。
删除代码和BST的删除相似，AVL删除元素后还要照顾好平衡。
bool DeletElement(BiTree&T,int key,bool&lower)//参数（0）树根，（1）删除的元素，（3）此树是否降低标志位
{
bool L,R;//删除的是左子树还是右子树，作为标志。
L=R=false;
if(T==NULL) // 判断树根是否为空
return false;
if(key==T->data)//找到了所要删除的节点
{
BitNode* p,*s;
p=T->rchild;
s=p;
lower=true; //找到了必定删除，lower为真
if(T->rchild==NULL) // 如果所要删除的节点的右孩子为空
{
p=T;
T=T->lchild; //直接删除比如删除上图的 4,9,10，
free(p);
lower=true;
return true;
}
else
{
while (s)//如果所要删除的T节点右子树不为空，就找T的后继，也就是T的右孩子左子树的最左叶节点
{
p=s;
s=s->lchild;
}
T->data=p->data;//替换T
DeletElement(T->rchild,p->data,lower);//删除掉T的后继
R=true;
}
}
else if(key<T->data)
{
DeletElement(T->lchild,key,lower);
L=true;
}
else
{
DeletElement(T->rchild,key,lower);
R=true;
}
if(lower)//如果有节点删除
{
if(L)//删除的是左节点
{
switch (T->bf)
{
case LH://没删之前LH，删后T->bf=EH;
T->bf=EH;
lower=true;
break;
case RH://没删之前RH，删后导致右不平衡，
RightBalance(T);
lower=false;
break;
case EH://没删之前EH，删后RH；
T->bf=RH;
lower=false;
break;
default:
break;
}
}
else
{
switch (T->bf)
{
case EH:
T->bf=LH;
lower=false;
break;
case RH:
T->bf=EH;
lower=true;
break;
case LH:
LeftBalance(T);
lower=false;
break;
default:
break;
}
}
}
}
好吧，请原谅我骗了你，你看到这时，已不止半小时了。但为你使你相信你是有能力看完的，我不得不做这个下贱的谎言。 我不期望你能全部都能按照我的思路写下去，因为我写的还不够好，哪怕你有一点收获，楼主也是值得的。
这篇关于请要相信我，30分钟让你掌握AVL树（平衡二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
