二分图的最大匹配 ————匈牙利算法 （转载了一个大神的趣味算法） poj3041(Asteroids)

本文主要是介绍二分图的最大匹配 ————匈牙利算法 （转载了一个大神的趣味算法） poj3041(Asteroids)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

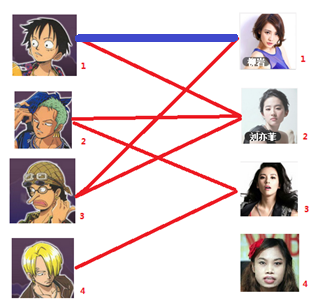
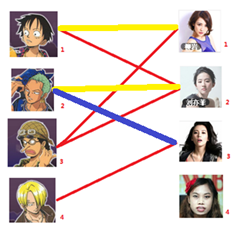
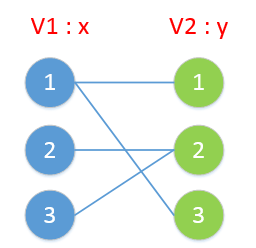
通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

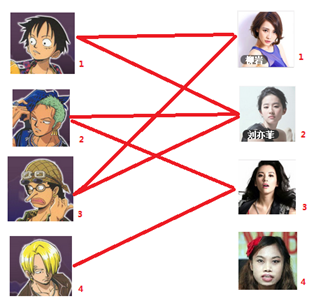
本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

===============================================================================

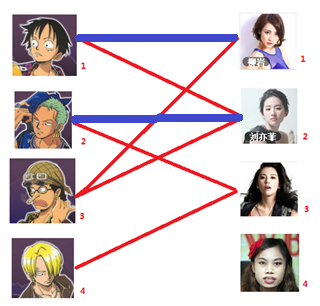
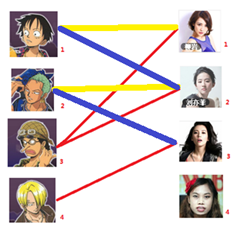
一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

===============================================================================

二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

===============================================================================

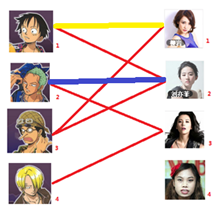
三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

(黄色表示这条边被临时拆掉)

与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

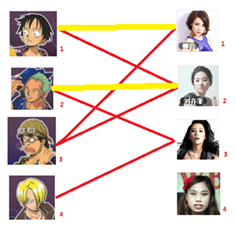
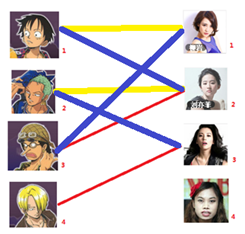
此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去

2号男生可以找3号妹子~~~                  1号男生可以找2号妹子了~~~                3号男生可以找1号妹子

所以第三步最后的结果就是：

===============================================================================

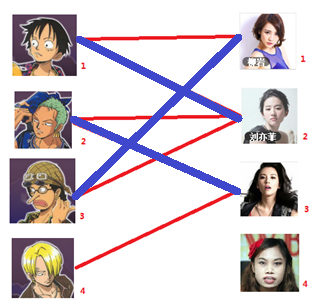
四： 接下来是4号男生，很遗憾，按照第三步的节奏我们没法给4号男生腾出来一个妹子，我们实在是无能为力了……香吉士同学走好。

===============================================================================

这就是匈牙利算法的流程，其中找妹子是个递归的过程，最最关键的字就是“ 腾”字

其原则大概是：有机会上，没机会创造机会也要上

bool find(int x){int i,j;for (j=1;j<=m;j++){    //扫描每个妹子if (line[x][j]==true && used[j]==false)      //如果有暧昧并且还没有标记过(这里标记的意思是这次查找曾试图改变过该妹子的归属问题，但是没有成功，所以就不用瞎费工夫了）{used[j]=1;if (girl[j]==0 || find(girl[j])) { //名花无主或者能腾出个位置来，这里使用递归girl[j]=x;return true;}}}return false;
}

在主程序我们这样做：每一步相当于我们上面描述的一二三四中的一步

for (i=1;i<=n;i++)
{memset(used,0,sizeof(used));    //这个在每一步中清空if find(i) all+=1;
}

Asteroids

Description

Input

Output

Sample Input

3 4
1 1
1 3
2 2
3 2

Sample Output

2

Hint

Source

思路：

将每行、每列分别看作一个点，对于case的每一个行星坐标（x，y），将第x行和第y列连接起来，例如对于输入：

（1，1）、（1，3）、（2，2）、（3，2）4点构造图G：

这样，每个点就相当于图G的一条边，消灭所有点=消灭图G的所有边，又要求代价最少，即找到图G上的最少的点使得这些点覆盖了所有边。

根据定理吗， 最小点覆盖数=最大匹配数，所以本题转化为二分图的最大匹配问题——用匈牙利算法来解决。

推荐一个好的讲解匈牙利算法的博文：《趣写算法系列之--匈牙利算法》

解题思路：

把方阵看做一个特殊的二分图（以行列分别作为两个顶点集V1、V2，其中| V1|=| V2|）

然后把每行x或者每列y看成一个点，而障碍物(x,y)可以看做连接x和y的边。按照这种思路构图后。问题就转化成为选择最少的一些点(x或y)，使得从这些点与所有的边相邻，其实这就是最小点覆盖问题。

再利用二分图最大匹配的König定理：

最小点覆盖数 = 最大匹配数

（PS：最小点覆盖：假如选了一个点就相当于覆盖了以它为端点的所有边，你需要选择最少的点来覆盖图的所有的边。）

因此本题自然转化为求 二分图的最大匹配 问题

求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。但是这个算法的时间复杂度为边数的指数级函数。

因此，需要寻求一种更加高效的算法——用增广路求最大匹配的方法（匈牙利算法）

增广路的定义(也称增广轨或交错轨)：

若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

　由增广路的定义可以推出下述三个结论：

1、P的路径个数必定为奇数，第一条边和最后一条边都不属于M。

2、将M和P进行取反操作可以得到一个更大的匹配M’

   （反操作：把P中的 匹配边 与 非匹配边 互换）

3、M为G的最大匹配当且仅当不存在M的增广路径P

　匈牙利算法轮廓：

(1)置M为空

(2)找出一条增广路径P，通过异或操作获得更大的匹配M’代替M

(3)重复(2)操作直到找不出增广路径为止

#include<iostream>
#include<fstream>using namespace std;int n, k;
int v1, v2;//二分图顶点集，都等于n
bool map[501][501];
bool visit[501]; //记录v2中的每个点是否被搜索过
int link[501]; //记录v2中的点y在v1中所匹配的点x的编号int result;//最大匹配数bool dfs(int x)
{for (int y = 1; y <= v2; y++){if (map[x][y] && !visit[y]){visit[y] = true;if (link[y] == 0 || dfs(link[y])){link[y] = x;return true;}}}return false;
}//匈牙利算法hungary algorithm
void search()
{for (int x = 1; x <= v1; x++){memset(visit,false,sizeof(visit));if (dfs(x)) //从v1中的节点x开始寻找增广路径presult++;}
}int main()
{//ifstream in("input.txt");cin >> n >> k;v1 = v2 = n;int x, y;memset(map,0,sizeof(map));for (int i = 1; i <= k; i++){cin >> x >> y;map[x][y] = true;}search();cout << result << endl;//system("pause");return 0;
}

这篇关于二分图的最大匹配 ————匈牙利算法 （转载了一个大神的趣味算法） poj3041(Asteroids)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！