各种系统零极点图的实现

各种系统零极点图的实现

% E_6_6.m

% 各种系统零极点图的实现

% 绘制情况(a)系统零极点分布图及系统单位序列响应

% 绘制情况(b)系统零极点分布图及系统单位序列响应

% 各种系统零极点图的实现
% 
% E_6_6.m
% 各种系统零极点图的实现
clc, clear, close all
figure
% 绘制情况(a)系统零极点分布图及系统单位序列响应
z = 0;          % 定义系统零点位置
p = 0.25;       % 定义系统极点位置
k = 1;          % 定义系统增益% 绘制系统零极点分布图
subplot(221); zplane(z,p); grid on;subplot(222); 
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
% 绘制系统单位序列响应时域波形图
impz(num,den);
% 定义标题
title('h(n)'); grid on;% 绘制情况(b)系统零极点分布图及系统单位序列响应
p = 1;
subplot(223); zplane(z,p); grid on;
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
% 求离散时间系统的单位冲激响应
impz(num,den);
subplot(224); title('h(n)'); grid on;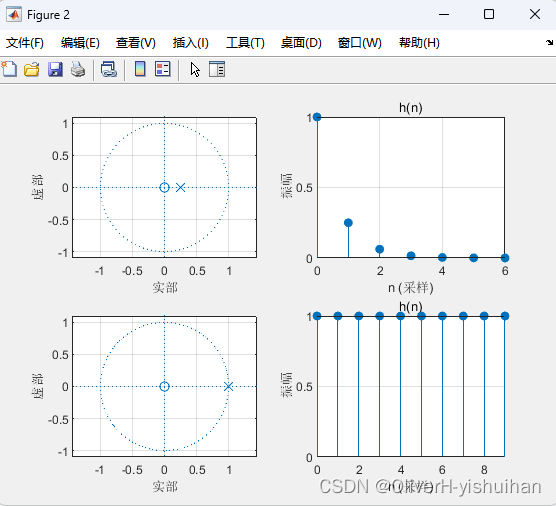

% 绘制情况(c)系统零极点分布图及系统单位序列响应

% 绘制情况(d)系统零极点分布图及系统单位序列响应

% 绘制情况(c)系统零极点分布图及系统单位序列响应
figure
% z = 0;          % 定义系统零点位置
% k = 1;          % 定义系统增益
p = -1.25;      % 定义系统极点位置
subplot(221); zplane(z,p); grid on;
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
% 求离散时间系统的单位冲激响应
impz(num,den,20);
subplot(222); title('h(n)'); grid on;% 绘制情况(d)系统零极点分布图及系统单位序列响应
% z = 0;          % 定义系统零点位置
% k = 1;          % 定义系统增益
p = [0.8*exp(pi*1i/6); 0.8*exp(-pi*1i/6)];      % 定义系统极点位置subplot(223); zplane(z,p); grid on;
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
% 求离散时间系统的单位冲激响应
impz(num,den,20);
subplot(224); title('h(n)'); grid on;

% 绘制情况(e)系统零极点分布图及系统单位序列响应

% 绘制情况(f)系统零极点分布图及系统单位序列响应

% 绘制情况(e)系统零极点分布图及系统单位序列响应
figure
% z = 0;          % 定义系统零点位置
% k = 1;          % 定义系统增益
p = [exp(pi*1i/8); exp(-pi*1i/8)];      % 定义系统极点位置
subplot(221); zplane(z,p); grid on;
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
subplot(222); impz(num,den,40);
title('h(n)'); grid on;% 绘制情况(f)系统零极点分布图及系统单位序列响应
% figure
% z = 0;          % 定义系统零点位置
% k = 1;          % 定义系统增益
p = [1.1*exp(3*pi*1i/16); 1.1*exp(-3*pi*1i/16)];      % 定义系统极点位置
subplot(223); zplane(z,p); grid on;
% 零极点模型转换为传递函数模型
[num,den] = zp2tf(z,p,k);
% 求离散时间系统的单位冲激响应
impz(num,den,40);
subplot(224); title('h(n)'); grid on;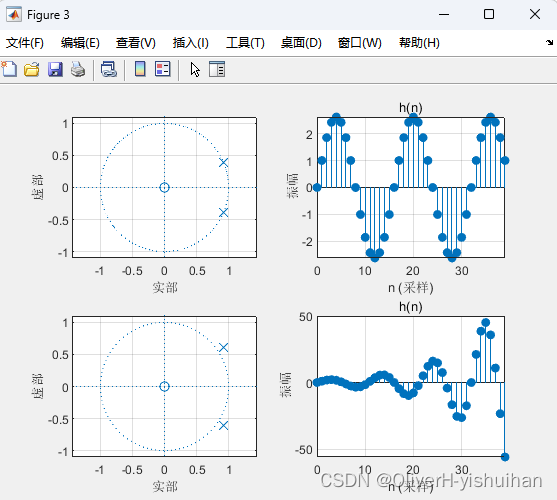

 结论：

            零极点距离越远，系统越不稳定。