LeetCode 319 Bulb Switcher（灯泡切换）（从规律中发现算法……）

本文主要是介绍LeetCode 319 Bulb Switcher（灯泡切换）（从规律中发现算法……），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

翻译

这儿有n个灯泡被初始化。首先，你点亮所有的灯泡。然后，你关掉每第二个灯泡。在第三回，你切换每第三个灯泡（如果它是关闭的则开启它，如果它是开启的则关闭它）。对于第i回，你切换每第i个灯泡。对于第n回，你仅仅切换最后一个灯泡。找出在n回之后还有多少个灯泡是亮着的。

原文

There are n bulbs that are initially off. You first turn on all the bulbs. Then, you turn off every second bulb. On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb. Find how many bulbs are on after n rounds.Example:Given n = 3. At first, the three bulbs are [off, off, off].
After first round, the three bulbs are [on, on, on].
After second round, the three bulbs are [on, off, on].
After third round, the three bulbs are [on, off, off]. So you should return 1, because there is only one bulb is on.

分析

我在本道题的第一阶段

我甚至都不能理解题目，什么叫every second bulb？又不是有一个二维数组（矩阵），如果把every second bulb理解成second bulb那最后岂不是只有第一个灯是亮着的了？

所以随便写了个函数试试：

class Solution {
public:int bulbSwitch(int n) {if(n == 0) return 0;return 1;}
};

于是LeetCode就告诉我如果输入是4，则应该返回2……继续：

class Solution {
public:int bulbSwitch(int n) {if(n == 0) return 0;if(n == 4) return 2;return 1;}
};

又告诉我如果输入是5，还是应该返回2。

于是在纸上演算了一下，结论是每两个的意思是第二个、第四个、第六个……

我在本道题的第二阶段

根据以上的思路，写出了如下算法，功能是实现了，体验却不好。LeetCode也告诉我如果是999999什么的，就超时了……

int bulbSwitch(int n) {bool* bulb = new bool[n];for (int i = 1; i <= n; ++i) {if (i == 1) {for (int j = 0; j < n; ++j)bulb[j] = true;}if (i > 1 && i < n) {for (int j = i; j < n; ) {bulb[j - 1] = bulb[j - 1] == true ? false : true;j += i;}}if (i == n) {bulb[n - 1] = bulb[n - 1] == true ? false : true;}}int result = 0;for (int i = 0; i < n; ++i) {if (bulb[i] == true)result += 1;}return result;
}

我在本道题的第三阶段

于是我就试图用位运算，把bool型的数组换成一个二进制的数字，二进制中的0和1正好表示bool数组，这样一来存储花费的空间就小了，效率也就高了。然而，我并没有完成……实在是有些复杂，以后可以继续尝试。

我在本道题的第四阶段

位运算没走通，就想走捷径了。为了清晰看到里面的变化过程，就全部打印了出来：

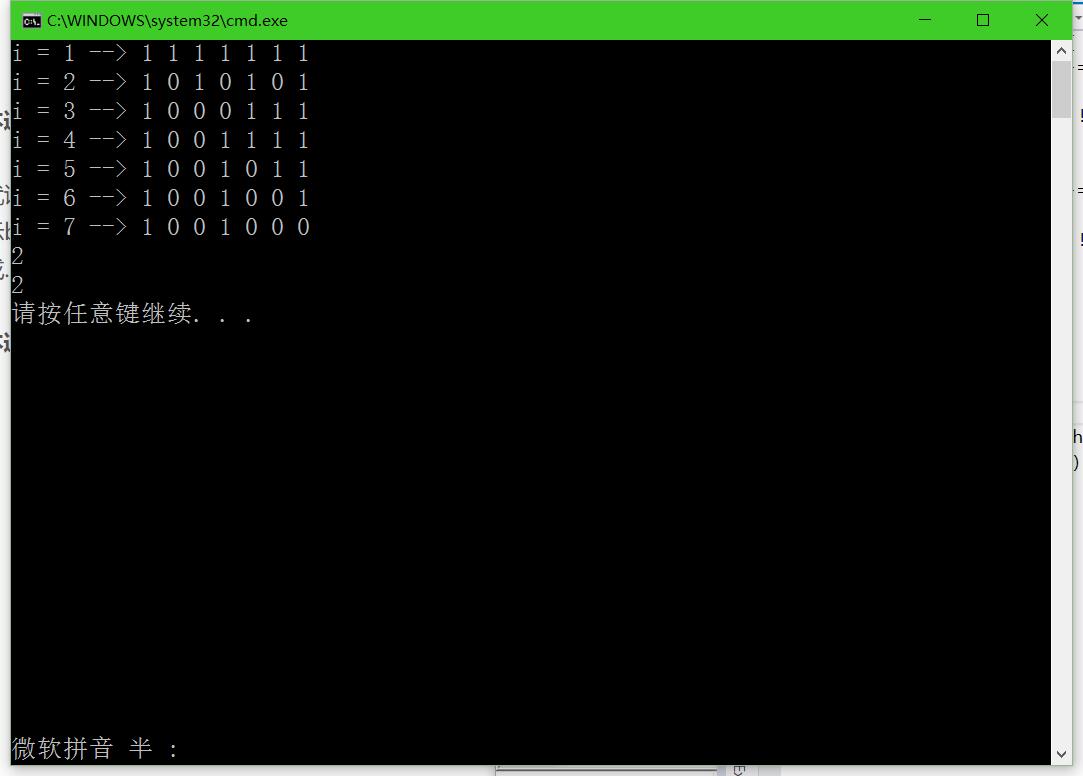
7的话好像还看不出来什么……

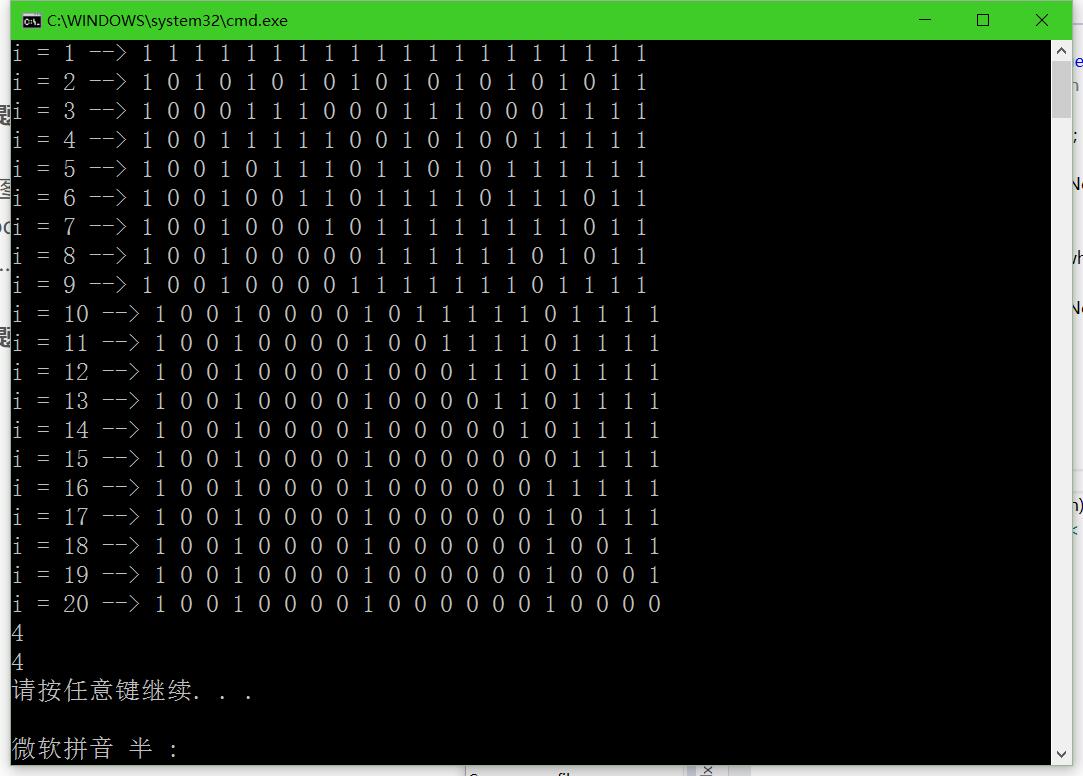
这里写图片描述

20的话，忽然发现了最底下，哎哟，有点意思啊……

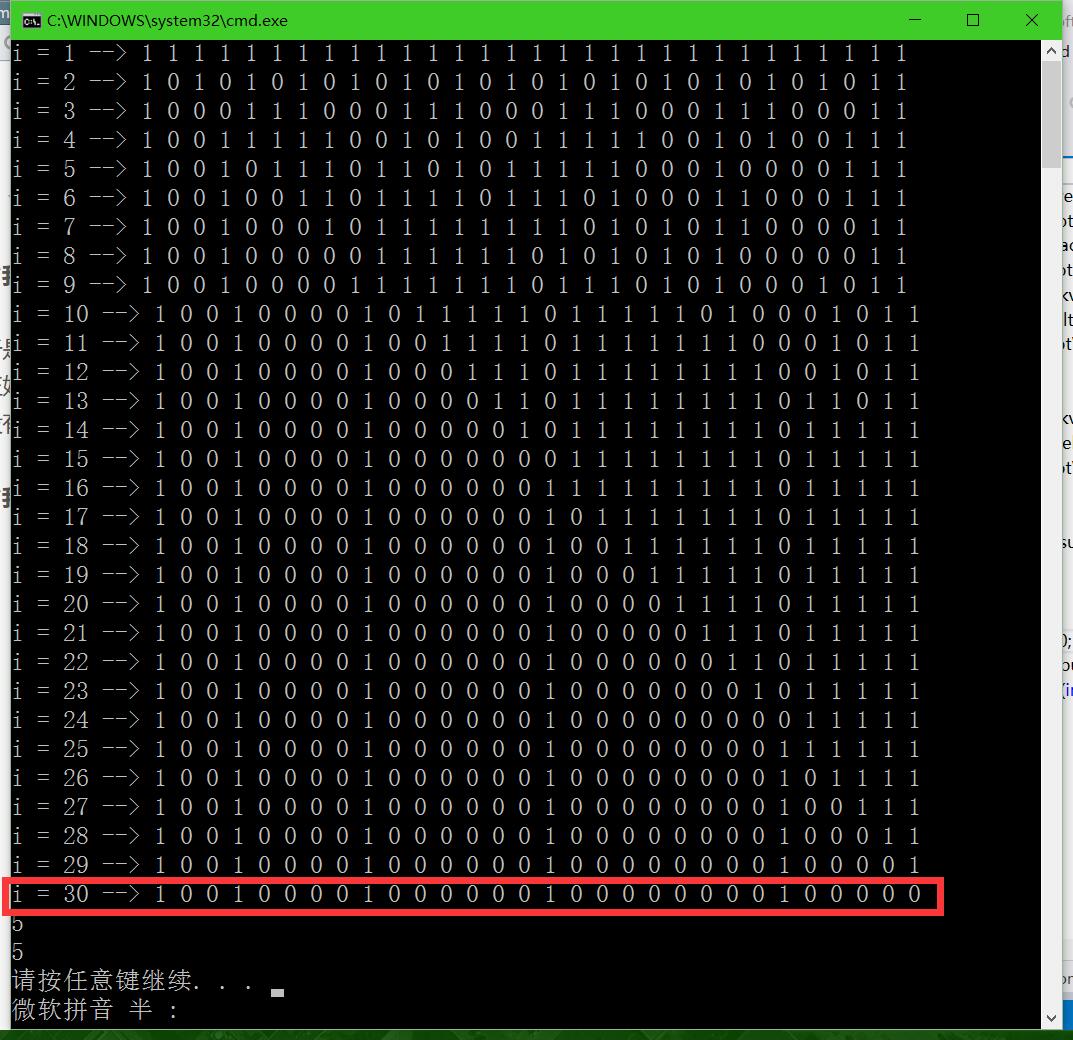
这里写图片描述

继续试了试30，于是就坚信了是这样的。

这里写图片描述

1 + 2 + 1 + 4 + 1 + 6 + 1 + 8 + 1 + 10 + 1

我把这个称为履带车，其中的“2，4，6，8……”称为轮子。

    int wheel = 2;int result = 0;int trackvehicle = 0;bool isNotWheel = true;

第一个轮子是从2开始的，result是最终的结果，trackvehicle是整个履带车的长度，isNotWheel作为初始的第一个并不是轮子（第二个、第四个才是轮子）。

Ok，逻辑也非常简单，直接上代码……

代码

class Solution {
public:
int bulbSwitch(int n) {int wheel = 2;int result = 0;int    trackvehicle = 0;bool isNotWheel = true;while ( trackvehicle < n ) {if (isNotWheel) {trackvehicle += 1;result += 1;isNotWheel = !isNotWheel;}else {trackvehicle += wheel;wheel += 2;                       isNotWheel = !isNotWheel;}   }return result;
}
};