二叉树---前中序数组建立唯一二叉树

本文主要是介绍二叉树---前中序数组建立唯一二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

二叉树的个数

具有n个结点的不同的二叉树有多少种？这与用栈得出的从1到n的数字有多少种不同的排列具有相同的结论。
那么，利用给定了一颗二叉树的前序序列（ABHFDECKG）和中序序列（HBDFAEKCG）能否唯一的确定一颗二叉树？

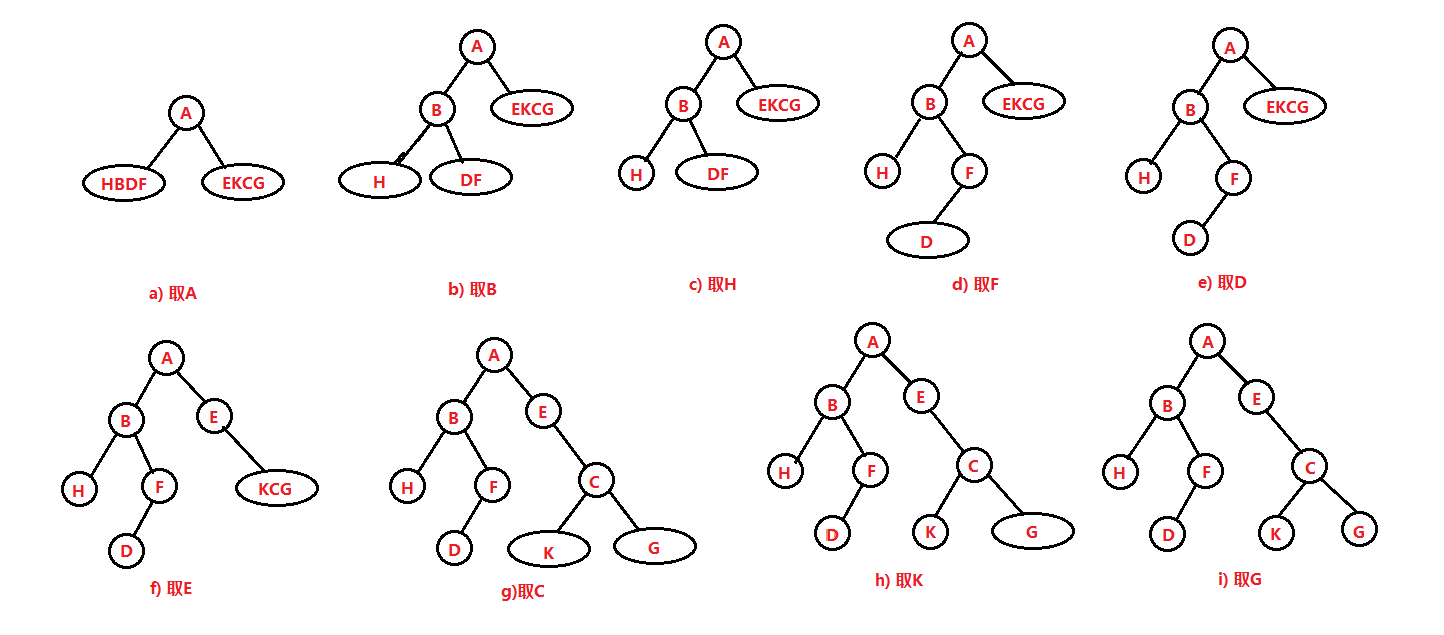
前序序列中，第一个字母A一定是数的根结点。中序序列中，被划分为两个子序列：((HBDF)A(EKCG)),这样与二叉树第一次近似。
然后，取前序序列的下一个字母B，它出现在A的左子树，应该是A左子树的根，它把中序子序列又划分成两个子序列：（（H）B（DF）），A结点的左子树与二叉树近似。
通过下面这张图就可以简单的理解利用前序序列和中序序列建立二叉树的过程。

前序序列（A B H F D E C K G）
中序序列（H B D F A E K C G）
这里写图片描述

代码实现

#include<queue>
#include<iostream>
using namespace std;template<class T>
struct BinTreeNode
{BinTreeNode<T> * _pLeft;BinTreeNode<T> * _pRight;T data;BinTreeNode(const T& data = 0 ):_pLeft(NULL), _pRight(NULL), data(data){}
};
template<class T>
class BinaryTree
{
public://构造函数BinaryTree():_pRoot(NULL){}//利用前序和中序数组，建立唯一二叉树BinTreeNode<T> * CreateBinTree_PreIn(T * VLR, T * LVR, int sz){if (VLR == NULL || LVR == NULL || sz <= 0)return NULL;int i = 0;//便利中序数组下标，找到根结点所在位置while (*VLR != LVR[i]){i++;}BinTreeNode<T> * t = new BinTreeNode<T>(LVR[i]);t->_pLeft = CreateBinTree_PreIn(VLR + 1, LVR, i);t->_pRight = CreateBinTree_PreIn(VLR + i + 1, LVR + i + 1, sz - i - 1);return t;}//前序遍历显示二叉树bool preOrder(BinTreeNode<T> * Node){if (Node == NULL)return false;preOrder(Node->_pLeft);printf("%d", Node->data);preOrder(Node->_pRight);}BinTreeNode<T> * get(){BinTreeNode<T> * ret = _pRoot;return ret;}private:BinTreeNode<T> * _pRoot;
};int main()
{BinaryTree<int>  s;BinTreeNode<int> * pRoot;int a[8] = { 1, 2, 3, 4, 5, 6, 7, 8 };/*s.CreateBinTree_Queue(a,8);pRoot = s.get();s.preOrder(pRoot);*/int VLR[9] = { 1, 2, 4, 8, 9, 5, 3, 6, 7 };int LVR[9] = { 8, 4, 9, 2, 5, 1, 6, 3, 7 };pRoot = s.CreateBinTree_PreIn(VLR, LVR, 9);s.preOrder(pRoot);return 0;
}