·新娘头饰复杂,这个婚礼怪异非凡。
·英文题,述大意:
婚宴上,有一个很长的桌子。桌子两边坐人(即人们坐成两排)。新娘坐在其中一排,只能看见桌子对面所有的人。输入的m表示有m对人打过架。在她快乐的眼睛里,不能出现以下情况:①有两个人是夫妻②有两个人打过架。询问是否存在一种座位编排方式满足条件。如果满足,还要输出与新娘同坐一排的人们(不含她)。
·分析:
本题两个限制条件,有一共同点:如果A坐在桌子这边,那么B就必须坐在桌子另一边。理论化地,若A为真,则B为假/若B为真,则A为假。这样两种情况可进一步简化为:A为假或者B为假。(亦即两者各属一方)
·考虑一个美妙的简化问题:
现有ABCD四个布尔变量,有以下要求:
“A为假或者B为假,B为假或者D为假,D为假或者C为假”
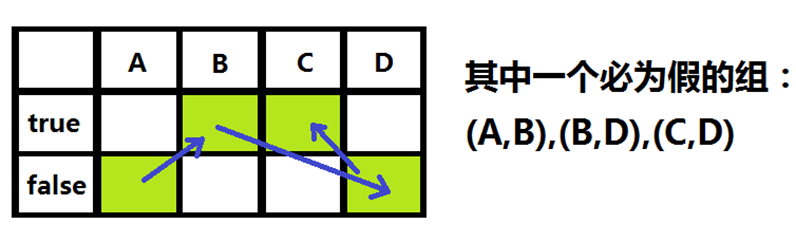
·如果我们令A为假,那么根据上述关系,就可以推出每个变量的值。
如果我们将这转化为一张图,每条边(u,v)表示如果u状态成立,那么v状态必须成立(例如:一条边可以是(A是假,B为真)),就可以很方便的用类似于染色的思想来完成:每走一步我们标记走过的结点,如果有一天标记的节点出现了(u为真)(u为假)两个点均被标记的情况,则说明是不合法的。
·细化思路:
重新注意“A为假或者B为假”。A为假不一定推出B一定为真,但是A为真就一定能推出B为假(2-SAT构图的关键)。因此,对于这样的条件,我们可以构造有向边:(A为真,B为假)。但是,如果你在慌乱之中构造了边:(A为假,B为真),那就错惨了(想一想,不为什么)。
·“构造一张有向图,其中每个变量i拆成2*i和i*2+1,分别表示该变量的假和真,最后要为每个变量选一种标记,使得整个图染色不会出现矛盾”
·我们统一所有的条件都是:“A为假或者B为假”。那么对于A,B标号的人,我们建边的方式为:(A*2+1,B*2)和(B*2+1,A*2)
·代码来临前的安宁:本题有一个“夫妻关系”,怎样处理?我们美妙地发现:如果将一对夫妇看成一个点,然后i*2,i*2+1直接表示这个点的真或假,我们再把真和假分别看成wife和husband,可以满足所有条件。不然,在正常情况下,夫妻要拆一次点,构造2-SAT要拆一次点,就不够美妙。如果偏要问在这个问题中,走到了点i*2或者i*2+1表达的是什么实际意义的话,那就是:走到了i*2表示第i对夫妇中,妻子和新娘坐一排;走到i*2+1表示丈夫和新娘坐一排。
1 #include<stdio.h>
2 #include<cstring>
3 #define go(i,a,b) for(int i=a;i<=b;i++)
4 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
5 #define mem(a,b) memset(a,b,sizeof(a))
6 const int N=50003;struct E{int v,next;}e[N*10];
7 int n,m,S[N],t,head[N],k;bool vis[N];
8 void ADD(int u,int v){e[k]=(E){v,head[u^1]};head[u^1]=k++;}
9 bool dfs(int u)
10 {
11 if(vis[u])return 1;if(vis[u^1])return 0;vis[u]=1;S[++t]=u;
12 fo(i,head,u)if(!dfs(v))return 0;return 1;
13 }
14 int main(){while(scanf("%d%d",&n,&m)&&n&&m)
15 {
16 mem(head,0);mem(vis,0);k=1;go(i,1,m){int u,v;char c;
17 scanf("%d%c",&u,&c);u=u*2+(c=='h');
18 scanf("%d%c",&v,&c);v=v*2+(c=='h');ADD(u,v);ADD(v,u);}
19
20 vis[0]=1;go(i,1,n-1){int u=i*2;if(vis[u]||vis[u+1])continue;
21 t=0;if(!dfs(u)){while(t)vis[S[t--]]=0;
22 if(!dfs(u+1)){printf("bad luck\n");goto Judy;}}}
23 go(i,1,n-1)printf("%d%c ",i,vis[i*2]?'w':'h');puts("");Judy:;
24 }return 0;}//Paul_Guderian
我们的那捧车菊花,由深绿变成了金黄;
穿过那青葱的岁月,体验着不羁的彷徨。————汪峰《闪亮的日子》







