CF935E Fafa and Ancient Mathematics

原题链接：http://codeforces.com/problemset/problem/935/E

Fafa and Ancient Mathematics

Ancient Egyptians are known to have understood difficult concepts in mathematics. The ancient Egyptian mathematician Ahmes liked to write a kind of arithmetic expressions on papyrus paper which he called as Ahmes arithmetic expression.

An Ahmes arithmetic expression can be defined as:

“$d$” is an Ahmes arithmetic expression, where $d$ is a one-digit positive integer;
“$(E1 op E2)$” is an Ahmes arithmetic expression, where $E_1$ and $E_2$ are valid Ahmes arithmetic expressions (without spaces) and $op$ is either plus ($+$ ) or minus ($-$).
For example $5, (1-1)$ and $((1+(2-3))-5)$ are valid Ahmes arithmetic expressions.
On his trip to Egypt, Fafa found a piece of papyrus paper having one of these Ahmes arithmetic expressions written on it. Being very ancient, the papyrus piece was very worn out. As a result, all the operators were erased, keeping only the numbers and the brackets. Since Fafa loves mathematics, he decided to challenge himself with the following task:

Given the number of plus and minus operators in the original expression, find out the maximum possible value for the expression on the papyrus paper after putting the plus and minus operators in the place of the original erased operators.

Input

The first line contains a string $E (1 ≤ |E| ≤ 10^4)$ — a valid Ahmes arithmetic expression. All operators are erased and replaced with ‘?’.

The second line contains two space-separated integers $P$ and $M$ $(0 ≤ min(P, M) ≤ 100)$ — the number of plus and minus operators, respectively.

It is guaranteed that $P + M$ =  the number of erased operators.

Output

Print one line containing the answer to the problem.

Examples

input

(1?1)
1 0

output

2

input

(2?(1?2))
1 1

output

1

input

((1?(5?7))?((6?2)?7))
3 2

output

18

input

((1?(5?7))?((6?2)?7))
2 3

output

16

Note

The first sample will be $(1 + 1)  =  2$.

The second sample will be $(2 + (1 - 2))  =  1$.

The third sample will be $((1 - (5 - 7)) + ((6 + 2) + 7))  =  18$.

The fourth sample will be $((1 + (5 + 7)) - ((6 - 2) - 7))  =  16$.

题目大意

给出一个算式,由括号和小于$10$ 的正整数和问号组成，问号是算式中的符号,现给出原式中加号的个数$p$ 和减号的个数$m$，对于所有填放方式对应的结果,求最大值。

题解

这里要用到一种将算式转化为二叉树的技巧，每个叶子节点为算式的初始数值，非叶子节点则为运算符号，样例$2$转换出的二叉树如图所示：

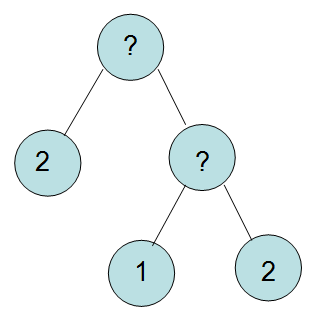
这样转化成二叉树之后，我们就可以做树形$dp$了，最简单的思路就是用$dp[i][j][k][0/1]$表示对于第$i$个点，它的子树中使用了$j$个加号，$k$个减号时子树运算式的最大/最小值。

但是，这种做法需要$O(|E|\times P\times M)$的空间，似乎开不下来，但是题目的数据范围$(0 ≤ min(P, M) ≤ 100)$似乎在暗示些什么。那么我们不妨把加号和减号的两维合并成一维，只记录数量较少的符号作为一维即可。

代码

#include<bits/stdc++.h>
#define ls son[v][0]
#define rs son[v][1]
using namespace std;
const int M=1e4+5;
int son[M][2],dad[M],dp[M][105][2],add,sub,len,minn,tot=1,pre=1;
char ch[M];
void build()
{len=strlen(ch+1),minn=min(add,sub);for(int i=1;i<M;++i)for(int j=0;j<=minn;++j)dp[i][j][0]=-1e9,dp[i][j][1]=1e9;for(int i=1;i<=len;++i)if(ch[i]=='('||ch[i]=='?')son[pre][son[pre][0]?1:0]=++tot,dad[tot]=pre,pre=tot;else if(ch[i]==')')pre=dad[pre];else dp[tot][0][0]=dp[tot][0][1]=ch[i]-'0',pre=dad[pre];
}
void dfs(int v)
{if(!ls)return;dfs(ls);dfs(rs);for(int i=0;i<=minn;++i)for(int j=0;i+j<=minn;++j)dp[v][i+j+(add<sub)][0]=max(dp[v][i+j+(add<sub)][0],dp[ls][i][0]+dp[rs][j][0]),dp[v][i+j+(add>=sub)][0]=max(dp[v][i+j+(add>=sub)][0],dp[ls][i][0]-dp[rs][j][1]),dp[v][i+j+(add<sub)][1]=min(dp[v][i+j+(add<sub)][1],dp[ls][i][1]+dp[rs][j][1]),dp[v][i+j+(add>=sub)][1]=min(dp[v][i+j+(add>=sub)][1],dp[ls][i][1]-dp[rs][j][0]);
}
void in(){scanf("%s%d%d",ch+1,&add,&sub);}
void ac(){build();dfs(1);printf("%d",dp[1][minn][0]);}
int main(){in();ac();}