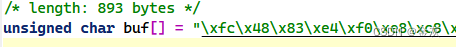【WC2011】bzoj2115 Xor

2023-11-07 20:08

文章标签 xor wc2011 bzoj2115

本文主要是介绍【WC2011】bzoj2115 Xor，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description

Input 第一行包含两个整数N和 M，表示该无向图中点的数目与边的数目。接下来M 行描述 M 条边，每行三个整数Si，Ti
，Di，表示 Si 与Ti之间存在一条权值为 Di的无向边。图中可能有重边或自环。 Output
仅包含一个整数，表示最大的XOR和（十进制结果）,注意输出后加换行回车。

因为一条路异或两次就没有了，所以任何一条路径的异或和，都可以看成是某条起点到终点的路径和若干个简单环异或的结果。
dfs一遍找出所有简单环和任意一条路径，对简单环权值求线性基再贪心选取。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define LL long long
int fir[50010],ne[200010],to[200010],n,m,tot,num;
bool vv[50010],ve[100010];
LL w[200010],f[50010],a[100010];
void add(int num,int u,int v,LL x)
{ne[num]=fir[u];fir[u]=num;to[num]=v;w[num]=x;
}
void init()
{int i,u,v;LL x;scanf("%d%d",&n,&m);for (i=1;i<=m;i++){scanf("%d%d%lld",&u,&v,&x);add(i*2,u,v,x);add(i*2+1,v,u,x);}
}
void dfs(int u)
{int i,v;for (i=fir[u];i;i=ne[i])if (!vv[v=to[i]]){vv[v]=ve[i/2]=1;f[v]=f[u]^w[i];dfs(v);}
}
void find()
{int i,j;for (i=1;i<=n;i++)for (j=fir[i];j;j=ne[j])if (!ve[j/2]){ve[j/2]=1;a[tot++]=f[i]^f[to[j]]^w[j];}
}
void solve()
{int i,p,j;LL ans;for (i=62,num=0;i>=0;i--){p=-1;for (j=num;j<tot;j++)if (a[j]&(1LL<<i)){p=j;break;}if (p==-1) continue;if (p>num) swap(a[p],a[num]);for (j=0;j<tot;j++)if (j!=num&&(a[j]&(1LL<<i)))a[j]^=a[num];num++;}ans=f[n];for (i=0;i<num;i++)if ((ans^a[i])>ans)ans^=a[i];printf("%lld\n",ans);
}
int main()
{init();vv[1]=1;dfs(1);find();solve();
}