本文主要是介绍数据结构 - 全貌总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一. 前言
二. 分类
三. 常见的线性和非线性结构
一. 前言
数据结构是计算机存储、组织数据的方式。一种好的数据结构可以带来更高的运行或者存储效率。数据在内存中是呈线性排列的,但是我们可以使用指针等道具,构造出类似“树形”等复杂结构。
数据结构主要分为逻辑结构、物理结构(存储结构)和运算三类。逻辑结构主要包含线性结构(如数组、队列、栈等)和非线性结构(如树、二叉树、堆等);物理结构包括顺序存储、链式存储、索引存储和散列存储;运算包括插入、删除、查找、排序等。
二. 分类
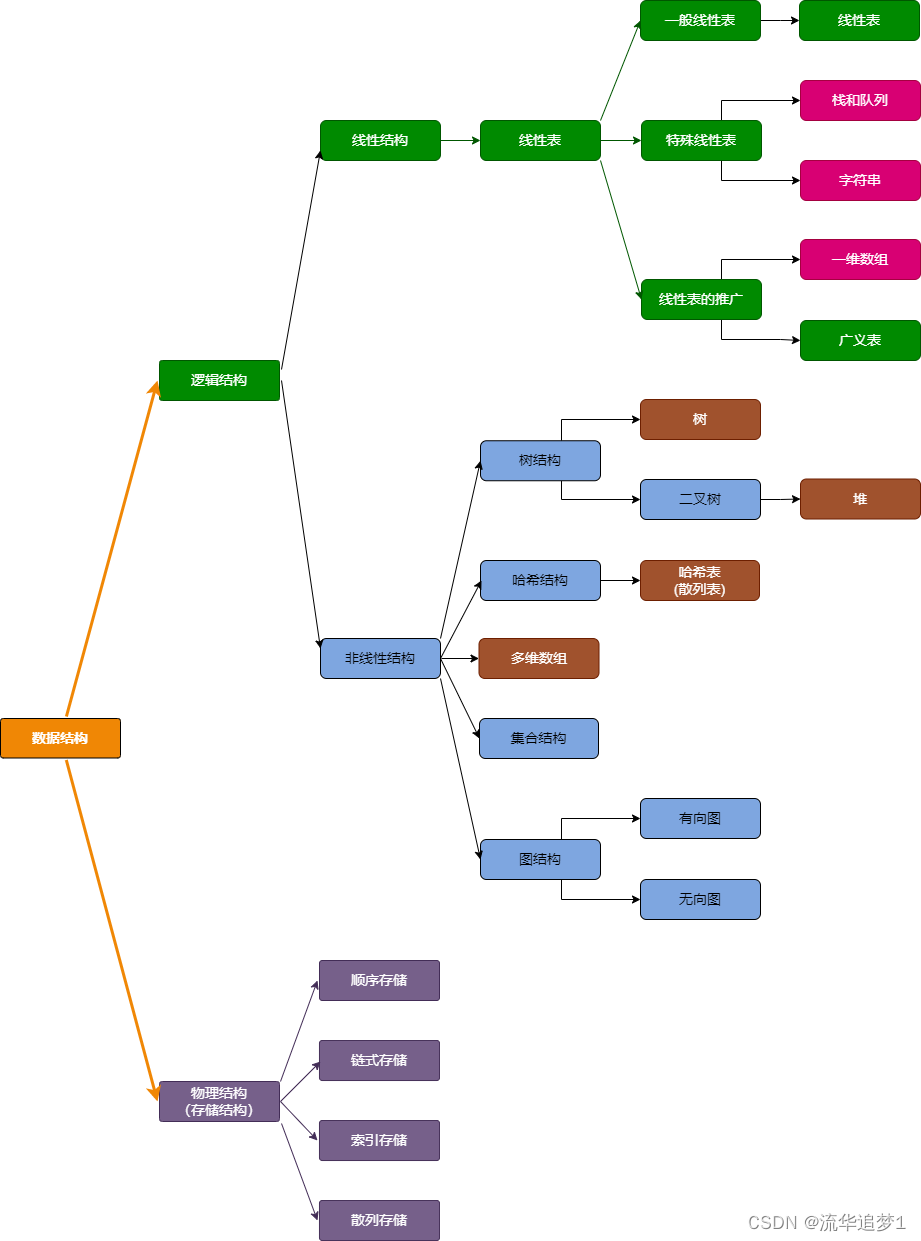
数组的下标寻址十分迅速,但计算机的内存是有限的,故数组的长度也是有限的,实际应用当中的数据往往十分庞大;而且无序数组的查找最坏情况需要遍历整个数组;后来人们提出了二分查找,二分查找要求数组的构造一定有序,二分法查找解决了普通数组查找复杂度过高的问题。任何一种数组无法解决的问题就是插入、删除操作比较复杂,因此,在一个增删查改比较频繁的数据结构中,数组不会被优先考虑。
普通链表由于它的结构特点被证明根本不适合进行查找。
哈希表是数组和链表的折中,同时它的设计依赖散列函数的设计,数组不能无限长、链表也不适合查找,所以也不适合大规模的查找。
二叉查找树因为可能退化成链表,同样不适合进行查找。
AVL树是为了解决可能退化成链表问题,但是AVL树的旋转过程非常麻烦,因此插入和删除很慢,也就是构建AVL树比较麻烦。
红黑树是平衡二叉树和AVL树的折中,因此是比较合适的。集合类中的Map、关联数组具有较高的查询效率,它们的底层实现就是红黑树。
多路查找树 是大规模数据存储中,实现索引查询这样一个实际背景下,树节点存储的元素数量是有限的(如果元素数量非常多的话,查找就退化成节点内部的线性查找了),这样导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。
B树与自平衡二叉查找树不同,B树适用于读写相对大的数据块的存储系统,例如磁盘。它的应用是文件系统及部分非关系型数据库索引。
B+树在B树基础上,为叶子结点增加链表指针(B树+叶子有序链表),所有关键字都在叶子结点 中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中。通常用于关系型数据库(如Mysql)和操作系统的文件系统中。
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针, 在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3。
R树是用来做空间数据存储的树状数据结构。例如给地理位置,矩形和多边形这类多维数据建立索引。
Trie树是自然语言处理中最常用的数据结构,很多字符串处理任务都会用到。Trie树本身是一种有限状态自动机,还有很多变体。什么模式匹配、正则表达式,都与这有关。
三. 常见的线性和非线性结构
数据结构中的逻辑结构分为线性和非线性两大类,主要有八大种,比如线性数据结构的就有 数组、链表、栈、队列。非线性的数据结构就有 树、堆、散列表、图等等。
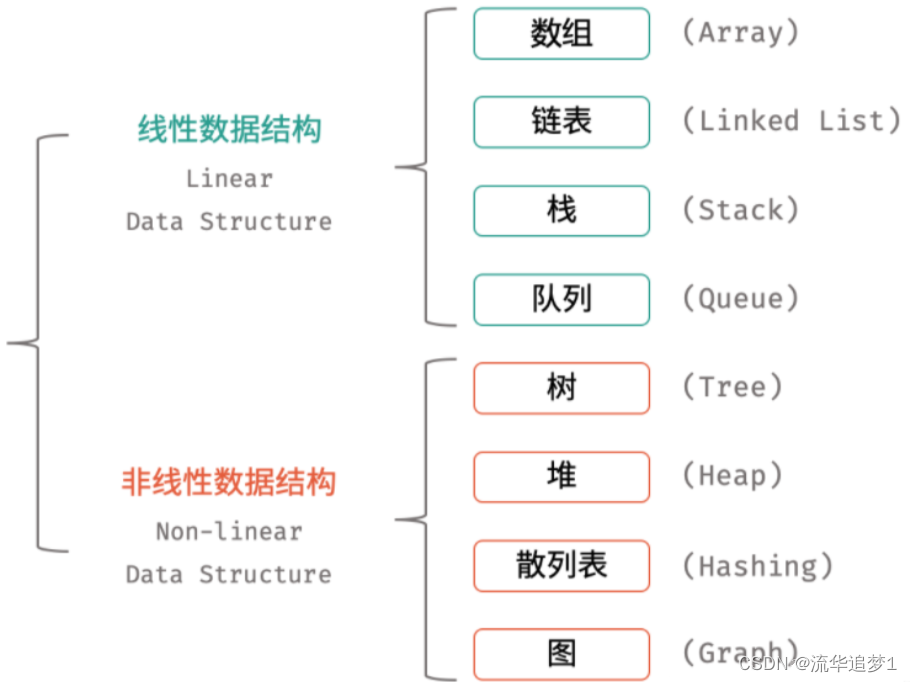
这篇关于数据结构 - 全貌总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





