noise1：A Universal Noise Removal Algorithm With an Impulse Detector

1.该篇论文介绍了一个脉冲噪声检测和降噪方法。

1）引入一种局部图像统计方法来识别被随机脉冲噪声破坏的像素。通过统计相邻像素在强度上的差异来实现。
2）将脉冲像素检测方法 集成到 双边滤波中，得到的滤波器可以去除脉冲噪声和高斯噪声。

2.什么是脉冲噪声

脉冲噪声（impulse noise）:是一定概率出现的噪声，对于一副图像，可能会有一定比例的像素出现脉冲噪声，因此脉冲噪声一般不是每个像素都有。

另外噪声像素 的 分布 一般是均匀分布，对于8bit图像可能是0-255中的任何值
其中有一种特殊情况，就是被噪声污染的点只可能是0，255，这种噪声又称椒盐噪声（salt-and-pepper noise）。

import numpy as npimport cv2
import matplotlib.pyplot as plt
def show_img4(im1, im2, im3, im4):plt.figure()plt.subplot(221)plt.imshow(im1)plt.subplot(222)plt.imshow(im2)plt.subplot(223)plt.imshow(im3)plt.subplot(224)plt.imshow(im4)plt.show()
def add_impulse_noise(im, p):im2 = im.copy()n = np.random.randint(0, 256, im.shape)sel = np.random.rand(*im.shape) < p # uniform distribution , [0,1)im2[sel] = n[sel]return im2def add_salt_and_pepper_noise(im, p):im2 = im.copy()n = np.random.randint(0, 2, im.shape)*255# print(n[:10,:10,0])sel = np.random.rand(*im.shape) < p # uniform distribution , [0,1)im2[sel] = n[sel]return im2
if __name__ == "__main__":file = r'G:\dataset\kodak\kodim03.png'im = cv2.imread(file)im = im[..., ::-1]im_impulse_noise = add_impulse_noise(im, 0.1)im_impulse_noise2 = add_impulse_noise(im, 0.4)im_impulse_noise3 = add_impulse_noise(im, 0.7)show_img4(im, im_impulse_noise, im_impulse_noise2, im_impulse_noise3)im_salt_and_pepper = add_salt_and_pepper_noise(im, 0.1)im_salt_and_pepper2 = add_salt_and_pepper_noise(im, 0.4)im_salt_and_pepper3 = add_salt_and_pepper_noise(im, 0.7)show_img4(im, im_salt_and_pepper, im_salt_and_pepper2, im_salt_and_pepper3)

添加脉冲噪声和椒盐后的结果图：

3.一般的脉冲噪声滤波算法分为检测和去除两个步骤，

大部分针对的是 椒盐噪声这种情况（文中称其离散的脉冲噪声，区别于 0-255均匀分布的脉冲噪声)。但是如果不是椒盐噪声则很难检测到，比如 只 偏离 一个比较小的值。
对此，作者引入一个策略来表示这个 像素是脉冲噪声的可能性（偏离度），可能性越大，越可能是脉冲噪声，因此可以把它当做脉冲噪声像素，提高过滤的强度，反之降低过滤的强度。

1）如何检测：

这里以3*3的邻域举例，公式中的m取 4，x是中心像素，y是邻域像素
a.计算和邻域的绝对差

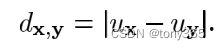
b. 计算m个最小的 绝对差 的和，这样其实就是找到领域和 中心像素最近的几个像素的差的 和，这个和在一定程度上反映了 当前像素是离散点（outlier点，脉冲噪声点）的可能性。

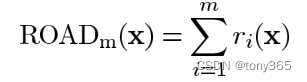
如下面图示意：
左上角是噪声点，比周围像素暗很多，因此得到的ROAD（m=4）也比较大为525
右下角非脉冲噪声点（或者噪声很小），ROAD（m=4）为88

c. 具体的ROAD计算流程就是上面所说的两个简单步骤
示意图如下：

2）如何过滤（自适应强度）

利用1）的方法检测像素点脉冲噪声的强度后，滤波强度也可以跟着变化，所以才是自适应的嘛。
这里引入双边滤波
双边滤波是邻域滤波，邻域的weight 不仅由像素点距离决定，还受 像素值的差异影响，与中心像素差异小的weight大，反之weight小。
如下图，Ws是距离weight, Wr是 值weight

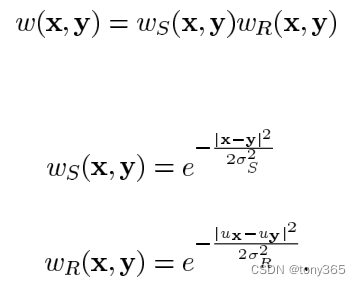
那么我们也可以定义一个脉冲噪声强度的weight.
x是脉冲噪声的可能性越大（偏离程度越大），WI 就越小，

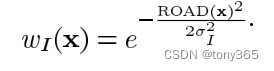
注意这里 WI的函数是评价邻域的像素点的脉冲噪声的。
如果是脉冲噪声，则赋予较小的weight，看下面公式，三者相乘就是该领域点的weight(先忽略 指数上标)

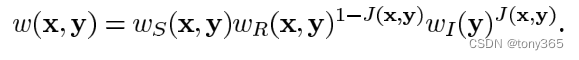
重点来了，WI 和 WR是互相矛盾的， 举例如果一个白色背景上有脉冲噪声暗点，WR会找到和他比较相近的暗点赋予高weight，WI 赋予其邻域暗点的则是低weight（因为邻域暗点的是脉冲噪声的可能性大）。

但是 WR项仍然可以保留，保留下来可以过滤那些 偏离较小的 像素点（非salt and pepper) ，这样我们可以通过 是脉冲噪声的可能性来控制 这两项的平衡。
当检测到是脉冲噪声时， WI 起更大作用，否则WR起更大作用。

这是通过J（x,y）项来实现的。
x,y只要有一个是脉冲噪声则J近似为1， WI起主要作用，赋予值差异大的邻域像素点较大的权重。
如果都不是脉冲噪声，近似为0， WR起主要作用，过滤轻度偏离的噪声点（脉冲噪声或者高斯噪声等噪声）

以上就是整个算法的原理了，双边滤波变成了三边滤波，保持原有的降噪（比如高斯）功能的同时具有了过滤脉冲噪声的功能

4. 参数如何选择

WS，WR，WI里面的sigma参数控制着形状，如何设置？
和噪声强度以及ROAD的强度是有关系的。
作者将
sigma_s对于高斯噪声设为 5，对于脉冲噪声设为 0.5
sigma_r设为 2倍的高斯噪声标准差（前提是你得首先估计出图像的噪声水平，这是另一个相关的算法领域了，文中用了一个比较早的方法）
sigma_i 设为40， 在[25,55]之间都基本满足。
sigma_J设为50， [30,80]之间也都OK

5. code和实验

上面左图为原图，有图 为添加 椒盐噪声20%和高斯噪声方差为10的混合噪声，
下面左图是双边滤波，右图是本人复现的代码降噪效果
可以看出还有个别 脉冲噪声没有被过滤掉

C-style的代码，运行时间可是真慢

def cal_road(im_gray, radiu=3):h, w = im_gray.shapeif radiu == 1:m = 5else:m = radiu * radiu // 3road = np.zeros(im_gray.shape, np.int32)for i in np.arange(radiu, h-radiu):for j in np.arange(radiu, w-radiu):c0 = im_gray[i, j]ro = []for ii in np.arange(-radiu, radiu+1):for jj in np.arange(-radiu, radiu+1):it = i + iijt = j + jjc1 = im_gray[it, jt]ro.append(abs(int(c1)-c0))ro = np.sort(np.array(ro))road[i, j] = int(np.sum(ro[:m]))# if i < 10 and j < 10:#     print(m, ro, sum(ro[:m]), road[i, j])return roaddef trilateral_filter(im_gray, road, radiu=1, sigma_s=5, sigma_r=20, sigma_i=40, sigma_j=50):im2 = im_gray.copy()h, w = im2.shapefor i in np.arange(radiu, h-radiu):for j in np.arange(radiu, w-radiu):c0 = im2[i, j]sum_v = 0w_v = 0for ii in np.arange(-radiu, radiu+1):for jj in np.arange(-radiu, radiu+1):it = i + iijt = j + jjc1 = im2[it, jt]a = (it-i)*(it-i) + (jt-j)*(jt-j)b = (int(c1) - c0)*(int(c1)-c0)ws = np.exp(-a / 2 / (sigma_s * sigma_s))wr = np.exp(-b / 2 / (sigma_r * sigma_r))c = road[it, jt] * road[it, jt]d = (road[it, jt] + road[i, j])**2wi = np.exp(-c / 2 / (sigma_i * sigma_i))J = 1 - np.exp(-d/8/(sigma_j * sigma_j))weight = ws * (wr**(1-J)) * (wi**J)sum_v += weight * c1w_v += weightim2[i, j] = np.round(sum_v / w_v).astype(np.int32)# if i < 10 and j < 10:#     print(i, j, sum_v, w_v, im2[i, j], im_gray[i, j])im2 = np.clip(im2, 0, 255).astype(np.uint8)return im2if __name__ == "__main__":file = r'G:\dataset\kodak\kodim03.png'im = cv2.imread(file)#im = cv2.resize(im, [200,200])im = im[..., ::-1]im_impulse_noise = add_impulse_noise(im, 0.2)im_impulse_noise2 = add_impulse_noise(im, 0.4)im_impulse_noise3 = add_impulse_noise(im, 0.7)#show_img4(im, im_impulse_noise, im_impulse_noise2, im_impulse_noise3)im_salt_and_pepper = add_salt_and_pepper_noise(im, 0.2)im_salt_and_pepper2 = add_salt_and_pepper_noise(im, 0.4)im_salt_and_pepper3 = add_salt_and_pepper_noise(im, 0.7)#show_img4(im, im_salt_and_pepper, im_salt_and_pepper2, im_salt_and_pepper3)im_mix_noise = add_gaussian_noise(im_salt_and_pepper, 10)r, g, b = cv2.split(im_mix_noise)radiu = 1road = cal_road(r, radiu)r_denoised = trilateral_filter(r, road, radiu,sigma_s=5, sigma_r=20, sigma_i=40, sigma_j=50)road = cal_road(g, radiu)g_denoised = trilateral_filter(g, road, radiu,sigma_s=5, sigma_r=20, sigma_i=40, sigma_j=50)road = cal_road(b, radiu)b_denoised = trilateral_filter(b, road, radiu,sigma_s=5, sigma_r=20, sigma_i=40, sigma_j=50)im_res = cv2.merge([r_denoised, g_denoised, b_denoised])im_bi = cv2.bilateralFilter(im_mix_noise, 3, 10, 5)show_img4(im, im_mix_noise, im_bi, im_res)