Travelling by Stagecoach

2023-11-05 23:20

文章标签 travelling stagecoach

本文主要是介绍Travelling by Stagecoach，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Travelling by Stagecoach（POJ No.2686）

有一个旅行家计划乘马旅行。他所在的国家共m个城市，在城市之间有若干道路相连。从某个城市沿着某条路到相邻的城市需要乘马。而乘马需要使用车票，每用一张车票只能通过一条道路。每张车票有马的匹数，从一个城市到另一个城市所需的时间等于城市之间的道路除以马的数量的结果，这位旅行家共有n张车票，第i张车票上的马的匹数是ti。一张车票只能使用一次，并且换乘所需时间忽略。求从城市a到城市b所需的最短时间。如果无法到达b则输出“Impossible”。

本题的思路与TSP相同
TSP：https://blog.csdn.net/qq_45769877/article/details/104336842

设dp[v][S]：表示在顶点v时，剩余的车票集合为S，到达终点的最短时间

在初始值上有所改变
dp[v][∅]=无穷 v≠终点
dp[v][∅]=0 v=终点

递归表达式
状态转移，是车票的递减
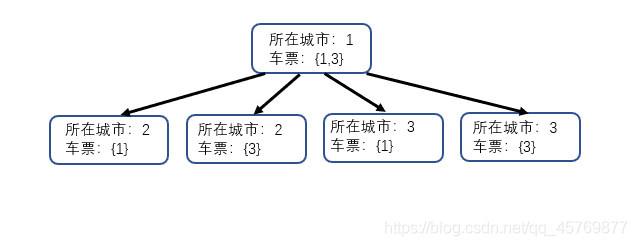
在这里插入图片描述
示例：

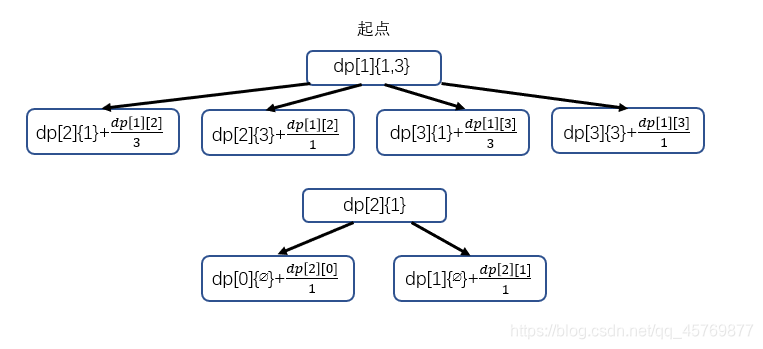
dp数组

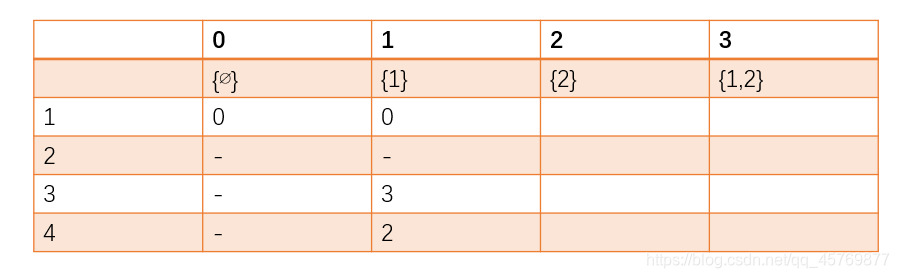
直接上代码

#include<iostream>
#include<stdlib.h>
#include<algorithm>
#define MAX_N 100
#define INF 1000
using namespace std;int n = 4, m = 2, a = 1, b = 0;
double t[MAX_N] = { 1,3 };
double d[4][4] = { {0,INF,3,2},{INF,0,3,5},{3,3,0,INF},{2,5,INF,0} };
double dp[MAX_N][MAX_N];void DP() {//当车票剩余为0时，若v为终点则值为0，在其他点时则不可能到达终点，值为INFfor (int i = 0; i < n; i++) {if (i == b) dp[i][0] = 0;else dp[i][0] = INF;}//以列为准，进行跟新for (int S = 1; S < 1 << m; S++) {for (int i = 0; i < n; i++) {//当v刚好为终点时，则其值为0if (i == b) dp[i][S] = 0;else {//对其他点进行计算dp[i][S] = INF;for (int j = 0; j < n; j++) {//对当前点v相邻的点，进行筛选if (d[i][j] != INF) {//对车票进行筛选for (int k = 0; k < m; k++) {if (((S >> k) & 1) == 1) {dp[i][S] = min(dp[i][S], dp[j][S ^ (1 << k)] + d[i][j] / t[k]);}}}}}}}
}
int main() {DP();//这里直接打印了dp数组for (int i = 0; i < n; i++) {for (int j = 0; j < (1 << m); j++)if (dp[i][j] == INF) cout << "INF\t";else cout << dp[i][j]<<"\t";cout << endl;}system("pause");
}