【VRP问题】基于遗传算法的连锁超市配送路线规划问题研究附matlab代码

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法       神经网络预测       雷达通信       无线传感器        电力系统

信号处理              图像处理               路径规划       元胞自动机        无人机 

⛄ 内容介绍

以数字型基础设施为代表的"新基建"目前处在起步阶段,面对经济下行的压力,夯实物流产业基础,可合理规划配送路线来提高物流配送效率.以合肥市某知名快递企业配送路径优化问题为研究对象,分析该企业配送问题,建立以配送网络成本最小为优化目标的数学模型,采用基本遗传算法的流程为模型设计算法,仿真运行得出结论.

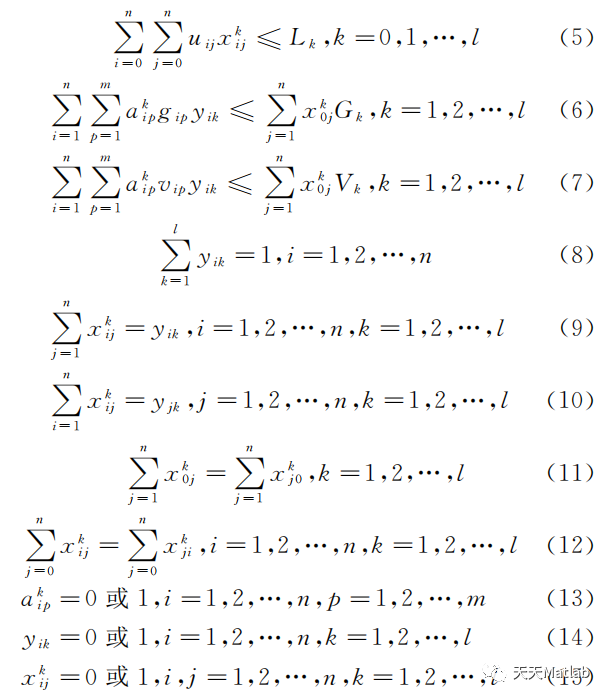
⛄ 部分代码

%% 画出最优配送方案路线图

%输入：bestVC,bestNV   配送方案

function draw_Best_num(bestVC,bestNV,center_pos,demand,vertexs,z)

hold on;box on

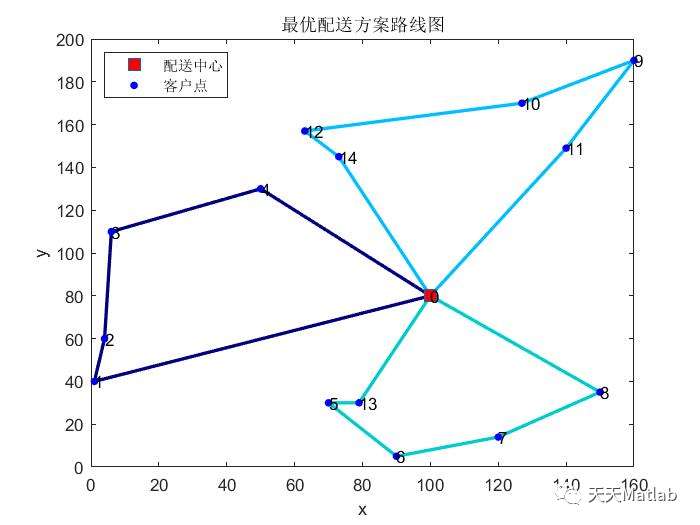
title('最优配送方案路线图')

disp(['优化结束！']);

disp(['~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~']);

disp(['优化的车辆使用数目为：',num2str(length(bestVC))]);

for i=1:length(bestVC)

fprintf('车辆');

fprintf('%d',i);

fprintf('的配送路径为：0 ->');

for j=1:length(bestNV{i})

fprintf('%d -> ',bestNV{i}(j));

end

fprintf('0\n');

end

hold on;

color_str=[0 0 0.5

    0 0.75 1

    0 0.8 0.8

    0 0.4 0

    1 0.84 0

    0.74 0.56 0.56

    0.8 0.36 0.36

    0.65 0.16 0.16

    1 0 0

    1 0 1

    0.6 0.2 0.8];

for i=1:length(bestVC)

    line([vertexs(1,1),vertexs(bestNV{i}(1)+1,1)],[vertexs(1,2),vertexs(bestNV{i}(1)+1,2)],'color',color_str(i,:),'linewidth',2);

    for j=1:length(bestNV{i})-1

        line([vertexs(bestNV{i}(j)+1,1),vertexs(bestNV{i}(j+1)+1,1)],[vertexs(bestNV{i}(j)+1,2),vertexs(bestNV{i}(j+1)+1,2)],'color',color_str(i,:),'linewidth',2);

    end

    line([vertexs(bestNV{i}(j+1)+1,1),vertexs(1,1)],[vertexs(bestNV{i}(j+1)+1,2),vertexs(1,2)],'color',color_str(i,:),'linewidth',2);

end   

plot_pos(center_pos,demand);

disp('此方案下各项成本计算如下：');

disp(['车辆派遣成本为：',num2str(z(1))]);

disp(['油耗成本为：',num2str(z(2))]);

disp(['时间惩罚成本为：',num2str(z(3))]);

disp(['车辆容量惩罚成本为：',num2str(z(4))]);

end

⛄ 运行结果

⛄ 参考文献

​[1]杨粟涵, 于蕾. 基于遗传算法的快递配送路径优化问题研究[J]. 现代信息科技, 2020, 4(9):3.

⛳️ 完整代码

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料