南邮数据结构实验3.5：飞机换乘最短距离(Dijkstra单源最短路径)

本文主要是介绍南邮数据结构实验3.5：飞机换乘最短距离(Dijkstra单源最短路径)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：编写程序，实现智能交通中的最佳路径选择问题：设有n个地点，编号为0~n-1，m条路径的起点、终点和代价由用户输入提供，采用实验3.1所示邻接矩阵为存储结构，寻找最佳路径方案(如花费时间最少、路径长度最短、交通费用最小等，任选其一即可)。

部分代码：

选出最小的d[i]：

//选出最小的d[i],i ∈ V-S
int Choose(int d[],int n,int s[]){  //对教材进行了一点改动,形式参数设置为数组而不是指针,参考了陈惠南老师的《数据结构——C语言描述》int i,minpos;ElemType min;min = INFTY;minpos = -1;for(i = 0;i < n;i ++){         //这里i初值改为0if(d[i] <= min && !s[i]){  //<改为<=min = d[i];minpos = i;}}return minpos;                //返回下标位置
}

Dijkstra算法：

//Dijkstra算法
Status Dijkstra(mGraph g,int v,int d[],int path[]){  //对教材进行了一点改动,形式参数设置为数组而不是指针,参考了陈惠南老师的《数据结构——C语言描述》int i,k,w,distance = 0;       //增加了一个distance记录最短距离之和int *s;if(v < 0||v > g.n-1){return ERROR;}s = (int*)malloc(g.n*sizeof(int));for(i = 0;i < g.n;i ++){      //初始化s[i] = 0;                 //表示顶点i是否在s中d[i] = g.a[v][i];         //v到i的距离if(i != v && d[i] < INFTY){path[i] = v;          //标识指向i的源点v}else path[i] = -1;}s[v] = 1;                     //顶点v为源点,将原点v加入集合Sprintf("%d ",v);              //输出源点0d[v] = 0;for(i = 1;i <= g.n-1;i ++){   //产生n-1条最短路径,<改为<=k = Choose(d,g.n,s);      //求当前路径最短者ks[k] = 1;                 //将k加入集合S中printf("%d ",k);for(w = 0;w < g.n;w ++){  //更新d和pathif(!s[w] && d[k]+g.a[k][w] < d[w]){d[w] = d[k] + g.a[k][w];distance = d[w];  //计算min距离path[w] = k;}}}printf("\nThe shortest distance:%d ",distance);return OK;
}

完整程序：

#include<stdio.h>
#include<stdlib.h>
#include <windows.h>
#define ERROR 0
#define OK 1
#define Overflow 2     //表示上溢
#define Underflow 3    //表示下溢
#define NotPresent 4   //表示元素不存在
#define Duplicate 5    //表示有重复元素
#define INFTY 32767    //表示极大值正无穷
typedef int ElemType;
typedef int Status;//邻接矩阵的结构体定义
typedef struct{ElemType **a;     //邻接矩阵int n;            //顶点数int e;            //边数ElemType noEdge;  //两顶点间无边时的值
}mGraph;//邻接矩阵的初始化
Status Init(mGraph *mg,int nSize,ElemType noEdgeValue){int i,j;mg->n = nSize;               //初始化顶点数mg->e = 0;                   //初始化时没有边mg->noEdge = noEdgeValue;    //初始化没有边时的取值mg->a = (ElemType**)malloc(nSize*sizeof(ElemType *));  //生成长度为n的一维指针数组if(!mg->a) return ERROR;for(i = 0;i < mg->n;i ++){   //动态生成二维数组mg->a[i] = (ElemType*)malloc(nSize*sizeof(ElemType));for(j = 0;j < mg->n;j ++){mg->a[i][j] = mg->noEdge;  //初始化时权重都设为-1}mg->a[i][i] = 0;        //自回路设置为0}return OK;
}//邻接矩阵的撤销(改成了int型，有返回值),先释放一维数组,再释放指针数组
int Destory(mGraph *mg){int i;for(i = 0;i < mg->n;i ++){free(mg->a[i]);  //释放n个一维数组的存储空间}free(mg->a);         //释放一维数组的存储空间return 1;
}//邻接矩阵的边的搜索
Status Exist(mGraph *mg,int u,int v){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v||mg->a[u][v] == mg->noEdge) return ERROR;return OK;
}//邻接矩阵的边的插入
Status Insert(mGraph *mg,int u,int v,ElemType w){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;if(mg->a[u][v] != mg->noEdge) return Duplicate;  //若待插入边已存在,则返回出错信息mg->a[u][v] = w;                                 //插入新边mg->e ++;                                        //增加一条边return OK;
}//邻接矩阵的边的删除
Status Remove(mGraph *mg,int u,int v){if(u < 0||v < 0||u > mg->n-1||v > mg->n-1 ||u == v) return ERROR;if(mg->a[u][v] == mg->noEdge) return NotPresent;  //若待删除边不存在,则返回出错信息mg->a[u][v] = mg->noEdge;                         //删除边mg->e --;return OK;
}//选出最小的d[i],i ∈ V-S
int Choose(int d[],int n,int s[]){  //对教材进行了一点改动,形式参数设置为数组而不是指针,参考了陈惠南老师的《数据结构——C语言描述》int i,minpos;ElemType min;min = INFTY;minpos = -1;for(i = 0;i < n;i ++){         //这里i初值改为0if(d[i] <= min && !s[i]){  //<改为<=min = d[i];minpos = i;}}return minpos;                //返回下标位置
}//Dijkstra算法
Status Dijkstra(mGraph g,int v,int d[],int path[]){  //对教材进行了一点改动,形式参数设置为数组而不是指针,参考了陈惠南老师的《数据结构——C语言描述》int i,k,w,distance = 0;       //增加了一个distance记录最短距离之和int *s;if(v < 0||v > g.n-1){return ERROR;}s = (int*)malloc(g.n*sizeof(int));for(i = 0;i < g.n;i ++){      //初始化s[i] = 0;                 //表示顶点i是否在s中d[i] = g.a[v][i];         //v到i的距离if(i != v && d[i] < INFTY){path[i] = v;          //标识指向i的源点v}else path[i] = -1;}s[v] = 1;                     //顶点v为源点,将原点v加入集合Sprintf("%d ",v);              //输出源点0d[v] = 0;for(i = 1;i <= g.n-1;i ++){   //产生n-1条最短路径,<改为<=k = Choose(d,g.n,s);      //求当前路径最短者ks[k] = 1;                 //将k加入集合S中printf("%d ",k);for(w = 0;w < g.n;w ++){  //更新d和pathif(!s[w] && d[k]+g.a[k][w] < d[w]){d[w] = d[k] + g.a[k][w];distance = d[w];  //计算min距离path[w] = k;}}}printf("\nThe shortest distance:%d ",distance);return OK;
}int main(){mGraph g;int nSize,edge,u,v,i;int d[100];int path[100];ElemType w;printf("Please enter the size of the mgraph:");scanf("%d",&nSize);Init(&g,nSize,INFTY);printf("Please enter the number of the edges:");scanf("%d",&edge);printf("Now init the graph.\n");for(i = 0;i < edge;i ++){printf("Please enter the edge:");scanf("%d%d%d",&u,&v,&w);Insert(&g,u,v,w);}Dijkstra(g,0,d,path);return 0;
}

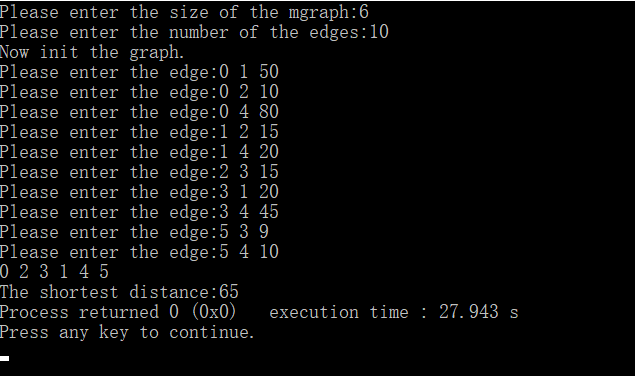
实验结果：