CF 1425 - E. Excitation of Atoms

本文主要是介绍CF 1425 - E. Excitation of Atoms，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接

题意：

给 $n$ 个原子。每个原子有两种状态，静态和激发态。每个原子 $i$ 从静态转换到激发态需要消耗 $d [i]$ 的能量，而在激发态会贡献的 $a [i]$ 的能量。初始的时候，序号从 $1 - n$ 的原子是按照编号顺序连接在一起的，也就是原子 $i$ 连接到原子 $i + 1$ 。在激发原子时有一个连锁反应，就是被激发的原子会自动激发它连接的下一个原子，这个时候是不会消耗能量的。但是最后一个原子不能连接到任何一个原子。

给定 $K$ ，我们必须要改变 $K$ 个连接关系。有一个限定是不能连接到自己，也不能连接到原来连接的原子。比如初始时，原子 $a$ 连接到原子 $b$ ，那么我们改变这个连接关系时，原子 $a$ 不能连接到原子 $a$ ，也不能再次连接原子 $b$ 。

我们可以选择激发任意多个原子，问最终能得到最大的能量是多少。

思路：

1）当 $K > = 2$ 时
①我们总是能将所有原子全部激发。我们可以选择激发前 $N - 1$ 个原子中（因为最后一个原子不能连接到任何的原子，所以不能作为激发原子）能量消耗 $d [i]$ 最小的那个原子 $i$ 以激发所有的原子。这样我们的收益就是：所有原子的能量和 - 原子 $i$ 能量消耗。
在这里插入图片描述

②我们还可以选择不改变原子的连接关系（虽然我们必须改变K次，但是我们可以改变了再改变回去哈哈哈），然后遍历激发每一个原子 $i$ , 取（后缀能量和 - 当前原子消耗）的最大收益 $m a x (s u f f i x [i] - d [i])$

2）当 $K = = 0$ 时
就只能不改变原来原子的连接关系，然后取 $m a x (s u f f i x [i] - d [i])$

3）当 $K = = 1$ 时

第一种情况：

我们枚举断点 $i$ , 断掉从点 $i$ 发出的边，然后将点 $i$ 连接到第一个点上（从2开始枚举，因为原子1不能连接到原子1）。然后这个原子就变成了两个部分： ① $[1, i]$ 的环； ② $[i + 1, N]$ 的链。
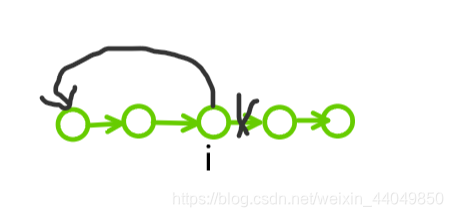
在这里插入图片描述

对于第一个部分，就和 $K > = 2$ 时的第一种情况类似，区间能量和-最小能量消耗即可。
对于第二个部分，就和 $K > = 2$ 时的第二种情况类似，直接找到 $m a x (s u f f i x [i] - d [i])$ 即可。
最后的结果自然就是两个部分相加了。

第二种情况：
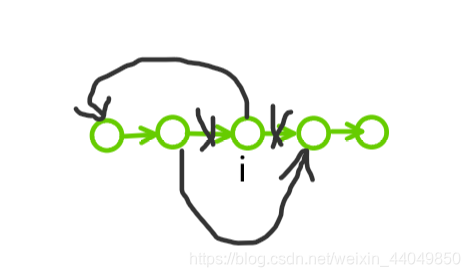
我们枚举断点 $i$ , 断掉从点 $i - 1$ 连接到 $i$ 的边，并且连接到 $i + 1$ 上。这样我们就成了一个如下图所示的样子。
在这里插入图片描述
这样的话我们考虑激发点在断点 $i$ 前 $[1, i - 1]$ ，还是在其后 $[i, N]$ 。

如果在断点后，那就很简单就是像 $K > = 2$ 时的第二种情况，直接找到 $m a x (s u f f i x [i] - d [i])$ 即可。

如果在断点前，我们就需要找到 $[1, i - 1]$ 这个区间内的 $m a x (s u f f i x [i] - d [i])$ ，然后减去 $a [i]$ 。所以我们可以用线段树维护区间的 $m a x (s u f f i x [i] - d [i])$ 。这个时候需要考虑单独的结点 $i$ 是不是有贡献，如果有正的贡献就加上。

最后的结果自然是激发点取断点前和断点后的最大值。

【关于为什么只间隔一个点呢，对于在断点后激发无影响。但是对于在断点前激发，那么断点后的能量和是确定的，我们对比的实际上是断点前那一段的 $m a x (s u f f i x [i] - d [i])$ 。所以去掉更多的点，显然不是更优的策略。】

tips!!!

对于每种情况都必须考虑不激发的情况，也就是每种情况的结果都要和 $0$ 对比取最大值。

Code:

#include <bits/stdc++.h>#define MID (l + r) >> 1
#define lsn rt << 1
#define rsn rt << 1 | 1
#define Lson lsn, l, mid
#define Rson rsn, mid + 1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll ;ll read() {ll res = 0, f = 1; char ch = getchar();while(ch < '0' || ch > '9') { if(ch == '-') f = -f; ch = getchar(); }while(ch >= '0' && ch <= '9') { res = res * 10 + ch - '0'; ch = getchar(); }return res * f;
}
const int maxN = 100005;int N, K;
int a[maxN], d[maxN];
ll prefix[maxN];
ll _min[maxN];
ll dp[maxN]; //后缀
ll tree[maxN << 2];
void pushup(int rt) {tree[rt] = max(tree[lsn], tree[rsn]);
}
void build_tree(int rt, int l, int r) {if(l == r) {tree[rt] = prefix[N] - prefix[l - 1] - d[l];return ;}int mid = MID;build_tree(Lson);build_tree(Rson);pushup(rt);
}
ll query(int rt, int l, int r, int ql, int qr) {if(ql <= l && qr >= r) {return tree[rt];}int mid = MID;if(qr <= mid) return query(QL);if(ql > mid) return query(QR);return max(query(QL), query(QR));
}
int main () {N = read(), K = read();for(int i = 1; i <= N; ++ i ) { //收益a[i] = read();prefix[i] = prefix[i - 1] + (ll)a[i];}for(int i = 1; i <= N; ++ i ) { //消耗d[i] = read();}ll MIN = d[1], min_pos = 1;_min[1] = min_pos;for(int i = 2; i < N; ++ i) {if(d[i] < MIN) {MIN = d[i];min_pos = i;}_min[i] = min_pos;}dp[N + 1] = -INF;for(int i = N; i >= 1; -- i ) {dp[i] = max(dp[i + 1], prefix[N] - prefix[i - 1] - (ll)d[i]);}build_tree(1, 1, N);ll ans = 0;if(K >= 2){ans = max(ans, prefix[N] - d[_min[N - 1]]);ans = max(ans, dp[1]);} else if(K == 0) {ans = max(ans, dp[1]);} else {//连向第一个点for(int i = 2; i < N; ++ i ) {ll fir = prefix[i] - d[_min[i]]; if(fir < 0) fir = 0;ll sec = dp[i + 1]; if(sec < 0) sec = 0;ans = max(ans, fir + sec);}//连向后面的点for(int i = 2; i < N; ++ i ) { //枚举断点i，跳过i点 割掉i - 1到i的边,ll left = max(query(1, 1, N, 1, i - 1) - (ll)a[i] + max(0ll, ll(a[i] - d[i])), 0ll); //从断点前激发ll right = max(0ll, dp[i]); //从断点后激发ans = max(left, ans);ans = max(right, ans);}}cout << ans << endl;return 0;
}
/*
4 1
2 5 2 1
101 2 101 100ans: 74 0
5 3 2 2
13 8 5 1ans: 14 1
10 10 9 100
1 10 10 1000000ans: 119*/