DDPG之OU过程

Ornstein-Uhlenbeck过程浅析

        上周在实现DDPG的过程中，发现其中用到了一个没见过的随机过程，叫做Ornstein-Uhlenbeck过程，所以简单地去了解了一下，下面我们进行概要讨论。

        OU过程是一种序贯相关的过程，在DDPG中用于实现RL的探索，想想也对，毕竟RL也是一种序贯相关模型，引入序贯噪声也不无道理。先参考维基百科看看OU过程长什么样子，OU过程满足下面的随机微分方程：

        其中，，均为参数，为维纳过程。

        我们先写个代码试试：

class OrnsteinUhlenbeckActionNoise:def __init__(self, mu, sigma=0.2, theta=0.15, dt=1e-2, x0=None):self.theta = thetaself.mu = muself.sigma = sigmaself.dt = dtself.x0 = x0self.reset()def __call__(self):x = self.x_prev + self.theta * (self.mu - self.x_prev) * self.dt + \self.sigma * np.sqrt(self.dt) * np.random.normal(size=self.mu.shape)self.x_prev = xreturn xdef reset(self):self.x_prev = self.x0 if self.x0 is not None else np.zeros_like(self.mu)def __repr__(self):return 'OrnsteinUhlenbeckActionNoise(mu={}, sigma={})'.format(self.mu, self.sigma)

        我们画出其图像：

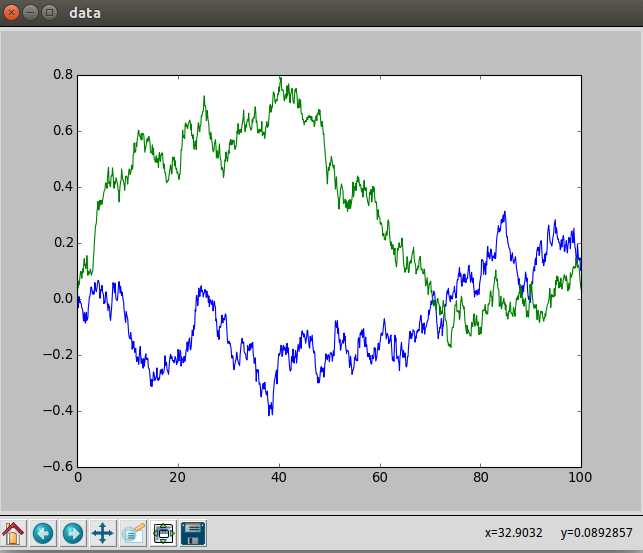
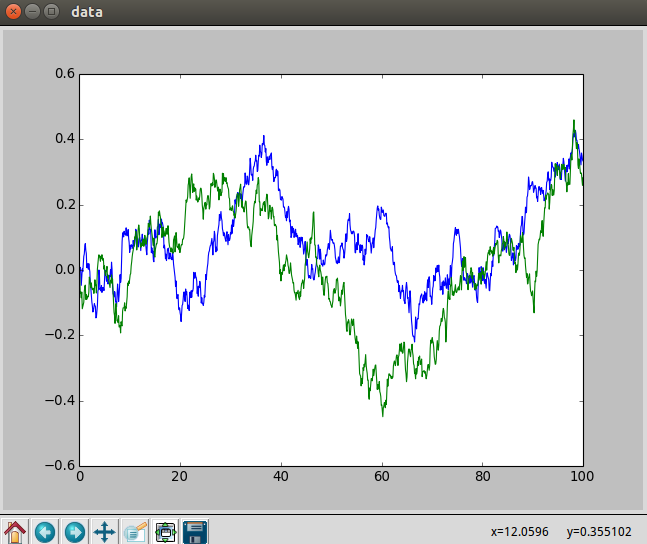
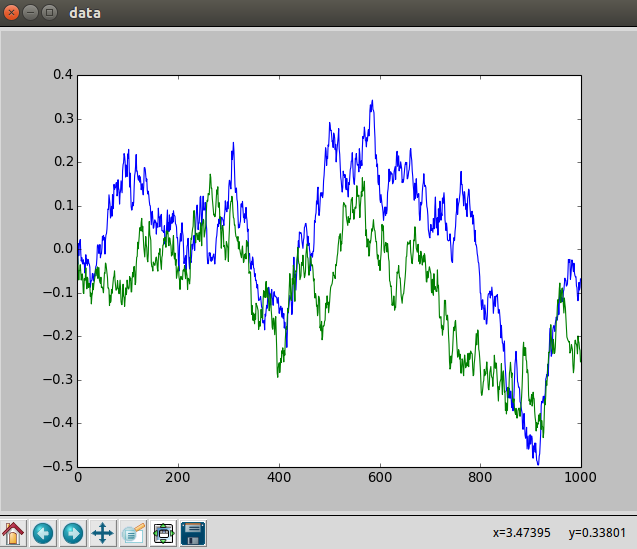
def main():ou_noise=OrnsteinUhlenbeckActionNoise(mu=np.zeros(2))plt.figure('data')y=[]t=np.linspace(0,100,1000)for _ in t:y.append(ou_noise())plt.plot(t,y)plt.show()if __name__=="__main__":main()

        恩，大概就是长这个样子，其中我们是对两个量施加的噪声，所以有两条曲线。

        随着时间的推移，这个过程将慢慢的漂移到它的long-term mean。

        好了，就这么浅......