5.单向链表的经典问题（C语言详解：约瑟夫环，拉丁方阵，魔术师发牌问题，判断链表是否有环）

2023-11-03 18:10
文章标签 语言 问题 链表 详解 判断 是否 经典 有环 约瑟夫 方阵 单向 拉丁 发牌 魔术师

本文主要是介绍5.单向链表的经典问题（C语言详解：约瑟夫环，拉丁方阵，魔术师发牌问题，判断链表是否有环），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

1.约瑟夫问题

      1.1经典的约瑟夫问题

      1.2更加复杂的约瑟夫问题

      1.3 用一维数组求解约瑟夫问题

2.拉丁方阵问题

3.判断单链表是否含有环

       3.1  比较步数法

       3.2  快慢指针法

4. 魔术师发牌问题

5.几个经典问题的编程实现

       5.1 C语言实现循环链表

       5.2 测试结果

6. 参考资料

1.约瑟夫问题

约瑟夫问题跟当下流行的吃鸡游戏非常类似，本身就是一个生存游戏，与吃鸡游戏不同的是，这个游戏靠的不是钢枪或者当伏地魔，而是用数学规则来决定生死！

      1.1经典的约瑟夫问题

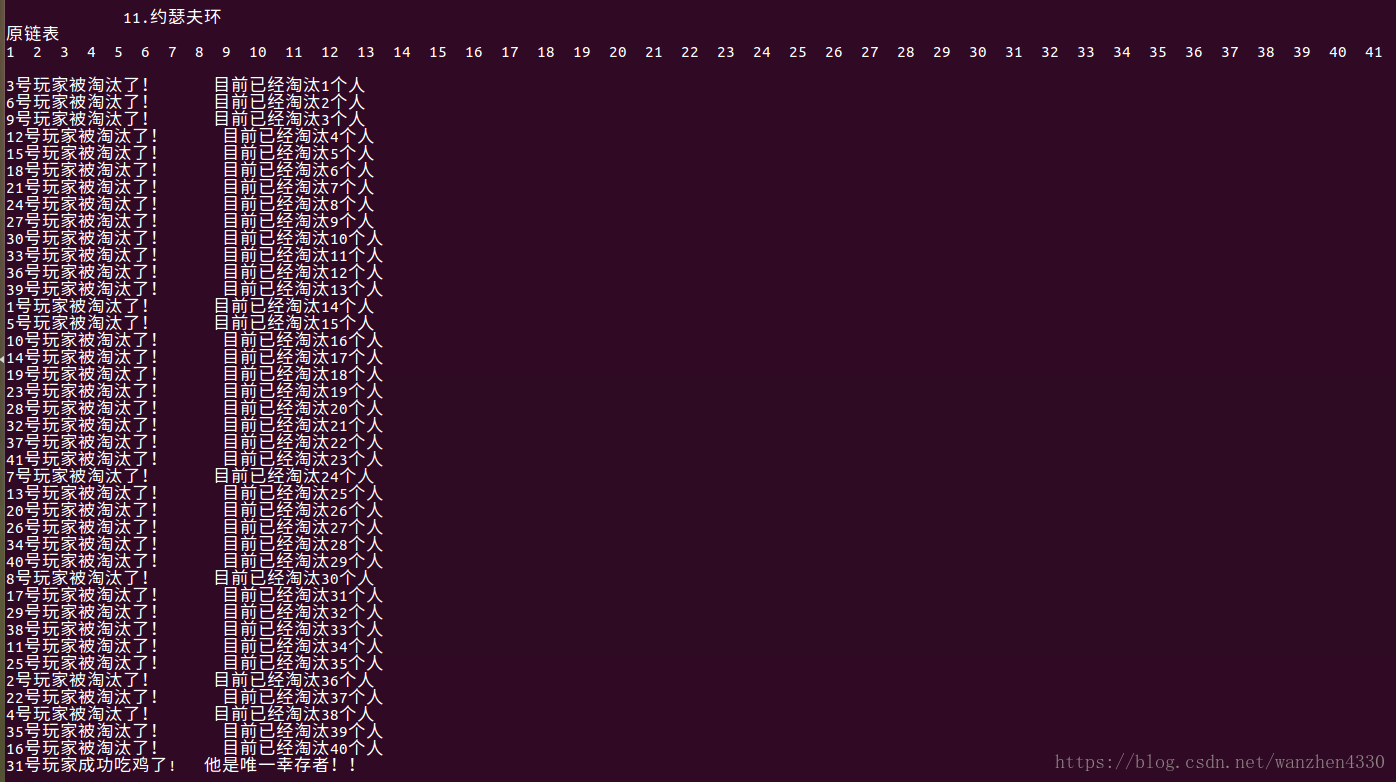
在罗马人占领乔塔特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从，Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

问题：用循环链表模拟约瑟夫问题，把41个人自杀的顺序编号输出。

解决方法：下图是核心程序，完整程序可以参考第4部分，有比较详细的注解。

typedef int ElemType;
typedef struct Node
{ElemType data;struct Node *Next;
}Node;typedef Node* linklist;//给节点指针取别名
typedef enum Bool
{FALSE,TRUE//枚举默认值从0开始，依次加1
}Bool;
void CreateListEnd(linklist* L,int n);//尾插法创建链表
void Josephus(linklist* L);//经典的约瑟夫问题void CreateListEnd(linklist* L,int n)//新建循环链表
{linklist p,rear;int i;(*L)=(linklist)malloc(sizeof(Node));if((*L)==NULL){printf("结点申请失败，初始化未完成！\n");exit(0);}(*L)->data=1;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=i+1;//rand()%100+1;p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;}
}void Josephus(linklist* L)//约瑟夫环
{linklist p;//指向待删结点的前面linklist q;int i=0;for(p=(*L)->Next;p->Next!=p;p=p->Next->Next)/*假设每次报数m个死一个人，则* 1.起始p从头向后移动m-2次；* 2.后续循环中，p每次向后移动m-1次。
* */{q=p->Next;p->Next=q->Next;printf("%d号玩家被淘汰了！      目前已经淘汰%d个人\n",q->data,++i);free(q);}printf("%d号玩家成功吃鸡了!   他是唯一幸存者！！\n\n\n",p->data);free(p);
}

      1.2更加复杂的约瑟夫问题

编号为1～N的N个人按顺时针方向围坐一圈，每人持有一个密码（正整数，可以自由输入），开始人选一个正整数作为报数上限值M，从第一个人按顺时针方向自1开始顺序报数，报道M时停止报数。报M的人出列，将他的密码作为新的M值，从他顺时针方向上的下一个人开始从1报数，如此下去，直至所有人全部出列为止。

问题：模拟这个问题的自杀编号。

基本思路：用含有两个数据域的循环链表来实现，第一个数据域data存放游戏者的编号，第二个数据域code存放此人的密码，程序设计与经典的约瑟夫问题基本相同。基本数据结构为：

typedef struct NodeCode
{int data;//玩家编号int code;//密码struct Node *Next;
}NodeCode;   //带密码的约瑟夫环的结点
typedef NodeCode* linklistcode;//给节点指针取别名

核心程序为：  

void CreateListEndCode(linklistcode* L,int n);//尾插法创建带密码的约瑟夫环
void printListCode(linklistcode L);//遍历约瑟夫环
void JosephusCode(linklistcode* L,int M);//更加复杂的约瑟夫问题void CreateListEndCode(linklistcode* L,int n)//尾插法创建带密码的约瑟夫环
{linklistcode p,rear;int i;(*L)=(linklistcode)malloc(sizeof(NodeCode));if((*L)==NULL){printf("结点申请失败，初始化未完成！\n");exit(0);}(*L)->data=1;//(*L)->code=rand()%100+1;//3;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklistcode)malloc(sizeof(NodeCode));p->data=i+1;//p->code=rand()%100+1;//3;//p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;//}
}void printListCode(linklistcode L)
{linklistcode p=L;if(L==NULL){printf("当前循环链表是空链表  \n\n\n");return;}printf("\n玩家编号%3d",p->data);//第一个结点的元素值for(p=p->Next;p!=L;p=p->Next)printf("%4d",p->data);printf("\n玩家密码%3d",L->code);//第一个结点的元素值for(p=L->Next;p!=L;p=p->Next)printf("%4d",p->code);printf("\n\n");
}void JosephusCode(linklistcode* L,int M)
{/*假设每次报数m个死一个人，则
* 1.起始p从头向后移动m-2次；
* 2.后续循环中，p每次向后移动m-1次。
*/linklistcode p=*L,q;//指向待删结点的前面int i,num;for(i=0;i<M-2;i++)p=p->Next;num=0;while(p->Next!=p){q=p->Next;p->Next=q->Next;printf("%d号玩家被淘汰了！      目前已经淘汰%d个人\n",q->data,++num);M=q->code;free(q);for(i=0;i<M-1;i++)p=p->Next;}printf("%d号玩家成功吃鸡了!   他是唯一幸存者！！\n\n\n",p->data);free(p);
}

      1.3 用一维数组求解约瑟夫问题

博主学习了魔术师发牌问题后，就想到了用一维数组模仿单链表，同时用标志位来标注每次被淘汰的人（0表示没有被淘汰，1表示已经被淘汰了）。下面是这种方法的源程序代码，n表示参加的总人数，数组cord存储的玩家的状态，下标+1表示玩家的编号，例如cord[i]如果为0就表示第i+1位（数组下标从0开始）玩家目前还活着；用取余运算来模拟循环链表结构：number=(number+1)%n；通过不断查找来确定每次被淘汰的玩家的编号，一旦第i+1位被淘汰，则cord[i]=1。下面是完整的源程序，其中n表示玩家总人数，m表示每次报多少个数，对于约瑟夫问题来说，n=41，m=3。

int Josephus(int n, int m)
{int* cord=(int*)malloc(n*sizeof(int));//类似于魔术师发牌问题：数组中0表示还在游戏中int count=0,number=-1;                 //淘汰的总人数for(int i=0;i<n;i++)cord[i]=0;while(count<n-1){for(int j=0;j<m;){number=(number+1)%n;if(cord[number]==0)j++;}cord[number]=1;//printf("%d  ",number);count++;}for(count=0;count<n;count++)if (cord[count]==0)return count;return -1;
}

 

2.拉丁方阵问题

拉丁方阵是大家熟知的数独的起源，规则比数独稍微简单一些。

问题描述：

拉丁方阵（英语：Latin square）是一种 n × n 的方阵，在这种 n × n 的方阵里，恰有 n 种不同的元素，每一种不同的元素在同一行或同一列里只出现一次。

当一个拉丁方阵的第一行与第一列的元素按顺序排列时，此为这个拉丁方阵的标准型，英语称为"reduced Latin square, normalized Latin square, 或Latin square in standard form"。因为标准型拉丁方阵非常简单，所以下面就实现标准型。

思路分析：

标准型拉丁方阵的基本特点是，第一行按1,2,3...n的顺序排列；第二行就是将第一行循环右移一位，即2,3,4，.....,n,1；以此类推，后续每一行的数据都是他的前一行数据循环右移一位形成的。标准型拉丁方阵的这种特点很适合用循环链表来实现：

void Latin(int n);
void Latin(int n)
{linklist list,head,p;//head每次后移一位，表示拉丁方阵每一行的新起点位置int i;CreateListEnd(&list,n);//创建单链表head=list;for(i=0;i<n;i++){p=head;printf("\n%d  ",p->data);//第一个结点的元素值for(p=p->Next;p!=head;p=p->Next)printf("%d  ",p->data);head=head->Next;}printf("\n\n");
}

3.判断单链表是否含有环

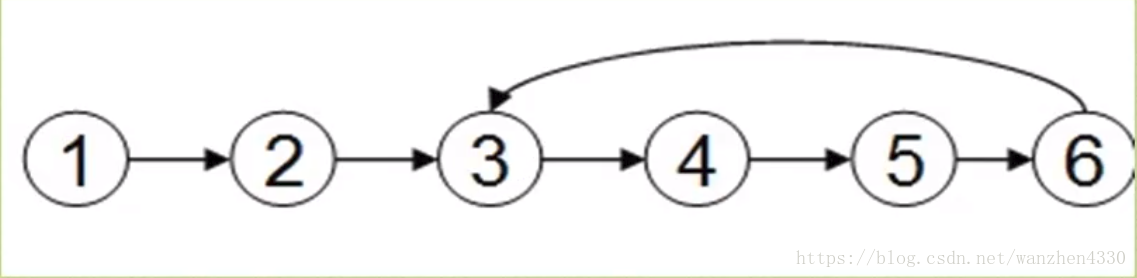
单链表中含有环的定义是，链表的尾节点指向了链表的某个结点，而不是指向空。例如下面的单链表就含有环： 

解决这个问题主要有两种方法：比较步数法，和快慢指针法。

       3.1  比较步数法

开始的时候有两个指针p和q，他们都指向链表第一个结点，p每次往后遍历一个结点，而q每次都从链表的第一个结点开始，p每往后遍历一次就比较二者相遇（二者指向同一个结点）各时自遍历的步数，当步数不同的时候，说明有环。核心程序如下：

Bool haveCirc1(linklist L)
{linklist p,q;int p_step,q_step,i=0;for(p=L,p_step=1;p!=NULL;p=p->Next,p_step++){for(q=L,q_step=1;q!=NULL;q=q->Next,q_step++){i++;if(p==q){if(q_step!=p_step){printf("该链表含有环，循环结点位置为：%d    循环语句执行%d次\n",q_step,i);return TRUE;}elsebreak;}}}printf("当前链表无环， 循环语句共执行了%d次\n",i);return FALSE;
}

       3.2  快慢指针法

刚开始的时候快慢指针都指向链表第一个结点，每次快指针向前走两步，而慢指针每次只往前走一步，当二者在运动的过程中发生相遇时，说明存在环。

Bool haveCirc2(linklist L)
{linklist fast,slow;int i;slow=fast=L;for(i=1;(fast->Next!=NULL)&&(fast->Next->Next!=NULL);){fast=fast->Next->Next;//fast的结点数依次为：3/5/7/9...if(fast==slow||fast->Next==slow)//fast的结点数依次为：3/5/7/9...，而slow为1/2/3/4...，无环时二者不可能相遇，fast更不可能出现在slow后面{printf("该链表含有环，循环语句执行%d次\n\n",i);return TRUE;}slow=slow->Next;//分别为1/2/3...i++;}printf("当前链表无环， 循环语句共执行了%d次\n\n",i-1);return FALSE;
}

4. 魔术师发牌问题

问题描述

一位魔术师掏出一叠扑克牌，魔术师取出其中13张黑桃，洗好后，把牌面朝下。说：“我不看牌，只数一数就能知道每张牌是什么？”魔术师口中念一，将第一张牌翻过来看正好是A；魔术师将黑桃A放到桌上，继续数手里的余牌，第二次数1，2，将第一张牌放到这叠牌的下面，将第二张牌翻开，正好是黑桃2，也把它放在桌子上。第三次数1，2，3，前面二张牌放到这叠牌的下面，取出第三张牌，正好是黑桃3，这样依次将13张牌翻出，全部都准确无误。

求解：魔术师手中牌的原始顺序是什么样子的？

基本思路

假设手中有13张牌，当牌没有翻开的时候可以给他标记为0，当牌翻开后标记为实际的数字。这样一来问题就变得简单了，可以使用循环链表来实现：首先创建一个长度为13的循环链表，链表中所有元素都是0，表示13张牌都是未知状态，然后给第一个元素标记上实际数字1，这时候第一张牌非0，只要是非0就表示这个位置的牌放在了桌子上，要从剩下的元素为0的12个结点中再数2个，给第2个标记上数字2；依次类推。。。

程序中需要注意的是，每次计数的时候只计数不在桌子上的牌，即链表中元素为0的结点。

核心程序如下：

void InitCards(linklist* L,int n);//尾插法创建全0链表
void MagicianDealingCards(linklist* L,int n);//确定每张牌的位置
void displayCards(linklist L);//将所有牌按顺序显示
void InitCards(linklist* L,int n)
{linklist p,rear;int i;(*L)=(linklist)malloc(sizeof(Node));(*L)->data=0;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=0;//rand()%100+1;p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;}
}void MagicianDealingCards(linklist* L,int n)
{linklist p=*L;int num,i;//每次发牌前计数的个数为num个p->data=1;for(num=2;num<=n;num++){for(i=0;i<num;){p=p->Next;if(p->data==0)//这个位置的牌已经放在桌子上了i++;}p->data=num;}
}void displayCards(linklist L)
{linklist p=L;char card[13]={'A','2','3','4','5','6','7','8','9','10','J','Q','K'};printf("黑桃%c  ",card[L->data-1]);//第一张肯定是Afor(p=p->Next;p!=L;p=p->Next)printf("黑桃%c  ",card[p->data-1]);printf("\n\n");
}

5.几个经典问题的编程实现

       5.1 C语言实现循环链表

（1）循环链表的声明 cirlinklist.h

#ifndef CIRLINKLIST_H
#define CIRLINKLIST_Htypedef int ElemType;
typedef struct Node
{ElemType data;struct Node *Next;
}Node;typedef Node* linklist;//给节点指针取别名
typedef enum Bool
{FALSE,TRUE//枚举默认值从0开始，依次加1
}Bool;typedef struct NodeCode
{int data;//玩家编号int code;//密码struct Node *Next;
}NodeCode;   //带密码的约瑟夫环的结点
typedef NodeCode* linklistcode;//给约瑟夫环的指针取别名void CreateListEnd(linklist* L,int n);//尾插法创建链表
void traverseList(linklist L);//遍历链表//1.约瑟夫环
void Josephus(linklist* L);//经典的约瑟夫问题
void CreateListEndCode(linklistcode* L,int n);//尾插法创建带密码的约瑟夫环
void printListCode(linklistcode L);//遍历约瑟夫环
void JosephusCode(linklistcode* L,int M);//更加复杂的约瑟夫问题//2.拉丁方阵
void Latin(int n);//3.判断链表是否有环
#if 0
判断是否有环的2种方法:
1.两个指针，p每次继续往后遍历一个结点，而q每次从头开始，记录二者相遇时（同一个结点，即结点的地址相同）各自遍历的步数，当步数不同的时候，说明有环；
2.用快慢指针的方法：快慢指针相遇的时候说明有环
#endif
void CreateSingleListEnd(linklist* L,int n);//尾插法创建单链表
void displaySingleList(linklist L);//显示单链表
void CreateCirListEnd(linklist* L,int n);//尾插法创建带环链表
void displayCirList(linklist L,int n);//显示循环链表，只循环显示n个元素即可
Bool haveCirc1(linklist L);//方法一：比较步数法
Bool haveCirc2(linklist L);//方法二：快慢指针法//4.魔术师发牌问题
/*0表示这张牌还没有翻开*/
void InitCards(linklist* L,int n);//尾插法创建全0链表
void MagicianDealingCards(linklist* L,int n);//确定每张牌的位置
void displayCards(linklist L);//将所有牌按顺序显示
#endif // CIRLINKLIST_H

（2） 循环链表的实现 cirlinklist.c

#include "cirlinklist.h"
#include <stdio.h>void traverseList(linklist L)
{linklist p=L;if(L==NULL){printf("当前循环链表是空链表  \n\n\n");return;}elseprintf("%d  ",p->data);//第一个结点的元素值for(p=p->Next;p!=L;p=p->Next){printf("%d  ",p->data);//        p=p->Next;}printf("\n\n");
}void CreateListEnd(linklist* L,int n)
{linklist p,rear;int i;(*L)=(linklist)malloc(sizeof(Node));if((*L)==NULL){printf("结点申请失败，初始化未完成！\n");exit(0);}(*L)->data=1;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=i+1;//rand()%100+1;p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;}
}void Josephus(linklist* L)
{linklist p;//指向待删结点的前面linklist q;int i=0;for(p=(*L)->Next;p->Next!=p;p=p->Next->Next)/*假设每次报数m个死一个人，则* 1.起始p从头向后移动m-2次；* 2.后续循环中，p每次向后移动m-1次。
* */{q=p->Next;p->Next=q->Next;printf("%d号玩家被淘汰了！      目前已经淘汰%d个人\n",q->data,++i);free(q);}printf("%d号玩家成功吃鸡了!   他是唯一幸存者！！\n\n\n",p->data);free(p);
}void CreateListEndCode(linklistcode* L,int n)//尾插法创建带密码的约瑟夫环
{linklistcode p,rear;int i;(*L)=(linklistcode)malloc(sizeof(NodeCode));if((*L)==NULL){printf("结点申请失败，初始化未完成！\n");exit(0);}(*L)->data=1;//(*L)->code=rand()%100+1;//3;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklistcode)malloc(sizeof(NodeCode));p->data=i+1;//p->code=rand()%100+1;//3;//p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;//}
}void printListCode(linklistcode L)
{linklistcode p=L;if(L==NULL){printf("当前循环链表是空链表  \n\n\n");return;}printf("\n玩家编号%3d",p->data);//第一个结点的元素值for(p=p->Next;p!=L;p=p->Next)printf("%4d",p->data);printf("\n玩家密码%3d",L->code);//第一个结点的元素值for(p=L->Next;p!=L;p=p->Next)printf("%4d",p->code);printf("\n\n");
}void JosephusCode(linklistcode* L,int M)
{/*假设每次报数m个死一个人，则
* 1.起始p从头向后移动m-2次；
* 2.后续循环中，p每次向后移动m-1次。
*/linklistcode p=*L,q;//指向待删结点的前面int i,num;for(i=0;i<M-2;i++)p=p->Next;num=0;while(p->Next!=p){q=p->Next;p->Next=q->Next;printf("%d号玩家被淘汰了！      目前已经淘汰%d个人\n",q->data,++num);M=q->code;free(q);for(i=0;i<M-1;i++)p=p->Next;}printf("%d号玩家成功吃鸡了!   他是唯一幸存者！！\n\n\n",p->data);free(p);
}void Latin(int n)
{linklist list,head,p;//head每次后移一位，表示拉丁方阵每一行的新起点位置int i;CreateListEnd(&list,n);//创建单链表head=list;for(i=0;i<n;i++){p=head;printf("\n%d  ",p->data);//第一个结点的元素值for(p=p->Next;p!=head;p=p->Next)printf("%d  ",p->data);head=head->Next;}printf("\n\n");
}void CreateSingleListEnd(linklist* L,int n)
{linklist p,end;int i;*L=(linklist)malloc(sizeof(Node));(*L)->data=1;end=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=i+1;//rand()%100+1;p->Next=NULL;end->Next=p;end=p;}
}void displaySingleList(linklist L)
{linklist p=L;while(p){printf("%d  ",p->data);p=p->Next;}printf("\n");
}void CreateCirListEnd(linklist* L,int n)
{linklist p,rear;int i;(*L)=(linklist)malloc(sizeof(Node));(*L)->data=1;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=i+1;//rand()%100+1;rear->Next=p;rear=rear->Next;//}rear->Next=(*L)->Next->Next->Next;//循环到第4个结点
}void displayCirList(linklist L,int n)
{linklist p=L;int i;if(L==NULL){printf("当前循环链表是空链表  \n\n\n");return;}printf("%d  ",p->data);//第一个结点的元素值for(i=1;i<n;i++){p=p->Next;printf("%d  ",p->data);}printf("\n");
}Bool haveCirc1(linklist L)
{linklist p,q;int p_step,q_step,i=0;for(p=L,p_step=1;p!=NULL;p=p->Next,p_step++){for(q=L,q_step=1;q!=NULL;q=q->Next,q_step++){i++;if(p==q){if(q_step!=p_step){printf("该链表含有环，循环结点位置为：%d    循环语句执行%d次\n",q_step,i);return TRUE;}elsebreak;}}}printf("当前链表无环， 循环语句共执行了%d次\n",i);return FALSE;
}Bool haveCirc2(linklist L)
{linklist fast,slow;int i;slow=fast=L;for(i=1;(fast->Next!=NULL)&&(fast->Next->Next!=NULL);){fast=fast->Next->Next;//fast的结点数依次为：3/5/7/9...if(fast==slow||fast->Next==slow)//fast的结点数依次为：3/5/7/9...，而slow为1/2/3/4...，无环时二者不可能相遇，fast更不可能出现在slow后面{printf("该链表含有环，循环语句执行%d次\n\n",i);return TRUE;}slow=slow->Next;//分别为1/2/3...i++;}printf("当前链表无环， 循环语句共执行了%d次\n\n",i-1);return FALSE;
}void InitCards(linklist* L,int n)
{linklist p,rear;int i;(*L)=(linklist)malloc(sizeof(Node));(*L)->data=0;//(*L)->Next=*L;//第一个结点rear=*L;for(i=1;i<n;i++){p=(linklist)malloc(sizeof(Node));p->data=0;//rand()%100+1;p->Next=*L;//新节点是新的尾节点，它指向头结点rear->Next=p;rear=rear->Next;}
}void MagicianDealingCards(linklist* L,int n)
{linklist p=*L;int num,i;//每次发牌前计数的个数为num个p->data=1;for(num=2;num<=n;num++){for(i=0;i<num;){p=p->Next;if(p->data==0)//这个位置的牌已经放在桌子上了i++;}p->data=num;}
}void displayCards(linklist L)
{linklist p=L;char card[13]={'A','2','3','4','5','6','7','8','9','10','J','Q','K'};printf("黑桃%c  ",card[L->data-1]);//第一张肯定是Afor(p=p->Next;p!=L;p=p->Next)printf("黑桃%c  ",card[p->data-1]);printf("\n\n");
}

（3）测试程序 main.c

#include <stdio.h>
#include "cirlinklist.h"int main()
{linklist list;int num;linklistcode listcode;printf("\n\n             11.约瑟夫环\n");CreateListEnd(&list,41);printf("原链表\n");traverseList(list);Josephus(&list);printf("\n\n             12.带密码的约瑟夫环\n");CreateListEndCode(&listcode,50);printf("原链表\n");printListCode(listcode);JosephusCode(&listcode,3);printf("\n\n             13.拉丁方阵\n");printf("请输入拉丁方阵的阶数：");scanf("%d",&num);Latin(num);printf("\n\n             14.判断链表是否含有环\n");linklist singlist,circlist;printf("\n测试单链表");CreateSingleListEnd(&singlist,10);displaySingleList(singlist);printf("方法一：逐个遍历法\n");haveCirc1(singlist);printf("\n方法二：快慢指针法\n");haveCirc2(singlist);printf("\n测试带环的链表");CreateCirListEnd(&circlist,10);displayCirList(circlist,10+2);//多显示两个，可以看到循环点的位置printf("方法一：逐个遍历法\n");haveCirc1(circlist);printf("\n方法二：快慢指针法\n");haveCirc2(circlist);printf("\n\n             15.魔术师发牌问题\n");linklist cards;InitCards(&cards,13);MagicianDealingCards(&cards,13);displayCards(cards);return 0;
}

       5.2 测试结果

（1）经典的约瑟夫环

（2）更加复杂的约瑟夫环

(3）拉丁方阵

(4) 判断单链表是否有环

(5)魔术师发牌问题

 

6. 参考资料

[1]小甲鱼的教学视频：https://www.bilibili.com/video/av2975983/?p=18

[2]百度百科，拉丁方阵：https://baike.baidu.com/item/%E6%8B%89%E4%B8%81%E6%96%B9%E9%98%B5/4413910

[3]百度经验，魔术师发牌问题：https://jingyan.baidu.com/article/0aa223755363c688cc0d6485.html

[4]单链表是否有环的基本思路：https://www.bilibili.com/video/av2975983/?p=19

这篇关于5.单向链表的经典问题（C语言详解：约瑟夫环，拉丁方阵，魔术师发牌问题，判断链表是否有环）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/339951。

相关文章

Java中StopWatch的使用示例详解

Java中StopWatch的使用示例详解

《Java中StopWatch的使用示例详解》stopWatch是org.springframework.util包下的一个工具类,使用它可直观的输出代码执行耗时,以及执行时间百分比,这篇文章主要介绍... 目录stopWatch 是org.springframework.util 包下的一个工具类，使用它
阅读更多...
Java进行文件格式校验的方案详解

Java进行文件格式校验的方案详解

《Java进行文件格式校验的方案详解》这篇文章主要为大家详细介绍了Java中进行文件格式校验的相关方案,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、背景异常现象原因排查用户的无心之过二、解决方案Magandroidic Number判断主流检测库对比Tika的使用区分zip
阅读更多...
Java实现时间与字符串互相转换详解

Java实现时间与字符串互相转换详解

《Java实现时间与字符串互相转换详解》这篇文章主要为大家详细介绍了Java中实现时间与字符串互相转换的相关方法,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、日期格式化为字符串（一）使用预定义格式（二）自定义格式二、字符串解析为日期（一）解析ISO格式字符串（二）解析自定义
阅读更多...
springboot security快速使用示例详解

springboot security快速使用示例详解

《springbootsecurity快速使用示例详解》：本文主要介绍springbootsecurity快速使用示例,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝... 目录创www.chinasem.cn建spring boot项目生成脚手架配置依赖接口示例代码项目结构启用s
阅读更多...
Python中随机休眠技术原理与应用详解

Python中随机休眠技术原理与应用详解

《Python中随机休眠技术原理与应用详解》在编程中,让程序暂停执行特定时间是常见需求,当需要引入不确定性时,随机休眠就成为关键技巧,下面我们就来看看Python中随机休眠技术的具体实现与应用吧... 目录引言一、实现原理与基础方法1.1 核心函数解析1.2 基础实现模板1.3 整数版实现二、典型应用场景2
阅读更多...
一文详解SpringBoot响应压缩功能的配置与优化

一文详解SpringBoot响应压缩功能的配置与优化

《一文详解SpringBoot响应压缩功能的配置与优化》SpringBoot的响应压缩功能基于智能协商机制,需同时满足很多条件,本文主要为大家详细介绍了SpringBoot响应压缩功能的配置与优化,需... 目录一、核心工作机制1.1 自动协商触发条件1.2 压缩处理流程二、配置方案详解2.1 基础YAML
阅读更多...
Python实现无痛修改第三方库源码的方法详解

Python实现无痛修改第三方库源码的方法详解

《Python实现无痛修改第三方库源码的方法详解》很多时候,我们下载的第三方库是不会有需求不满足的情况,但也有极少的情况,第三方库没有兼顾到需求,本文将介绍几个修改源码的操作,大家可以根据需求进行选择... 目录需求不符合模拟示例 1. 修改源文件2. 继承修改3. 猴子补丁4. 追踪局部变量需求不符合很
阅读更多...
java中反射(Reflection)机制举例详解

java中反射(Reflection)机制举例详解

《java中反射(Reflection)机制举例详解》Java中的反射机制是指Java程序在运行期间可以获取到一个对象的全部信息,：本文主要介绍java中反射(Reflection)机制的相关资料... 目录一、什么是反射？二、反射的用途三、获取Class对象四、Class类型的对象使用场景1五、Class
阅读更多...
golang 日志log与logrus示例详解

golang 日志log与logrus示例详解

《golang日志log与logrus示例详解》log是Go语言标准库中一个简单的日志库,本文给大家介绍golang日志log与logrus示例详解,感兴趣的朋友一起看看吧... 目录一、Go 标准库 log 详解1. 功能特点2. 常用函数3. 示例代码4. 优势和局限二、第三方库 logrus 详解1.
阅读更多...
一文详解如何从零构建Spring Boot Starter并实现整合

一文详解如何从零构建Spring Boot Starter并实现整合

《一文详解如何从零构建SpringBootStarter并实现整合》SpringBoot是一个开源的Java基础框架,用于创建独立、生产级的基于Spring框架的应用程序,：本文主要介绍如何从... 目录一、Spring Boot Starter的核心价值二、Starter项目创建全流程2.1 项目初始化（
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2