本文主要是介绍数字电子技术(一)数制和码制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
01数制和码制
- 绪论
- 信息与编码
- 数制(进制)转换
- 进制转换例题
- 二进制原码、反码、补码
- 二进制算数运算
- 常用编码
不同进制间的转换
原码、反码、补码间的转换
二进制数的补码运算
绪论
数字量:在时间、数量上是离散的,不连续的
电子技术:研究电子器件、电子器件的应用
电子器件:通过控制器件中电子的运动而进行工作
摩尔定律:一个硅片上的集成度
电子电路作用:处理信息、转换能量
IEEE:电气与电子工程师协会
IEC:国际电工协会
模拟电路:用连续的模拟电压/流值来表示信息
数字电路:用一个离散的电压序列来表示信息(任务:处理信息)
结构——接口——设计
信息与编码
编码的目的:处理信息
处理信息:解决不确定性
编码提出者:香农
encoding:唯一性,避免重复(千年虫Y2K问题)
数制:表示数量的规则(每一位的构成,高位到低位)
码制:表示事物的规则
目前数字电路中都采用二进制
表示数量时称二进制
表示事物时称二值逻辑
数制(进制)转换
-
进制:十进制D、二进制B、八进制O、十六进制H
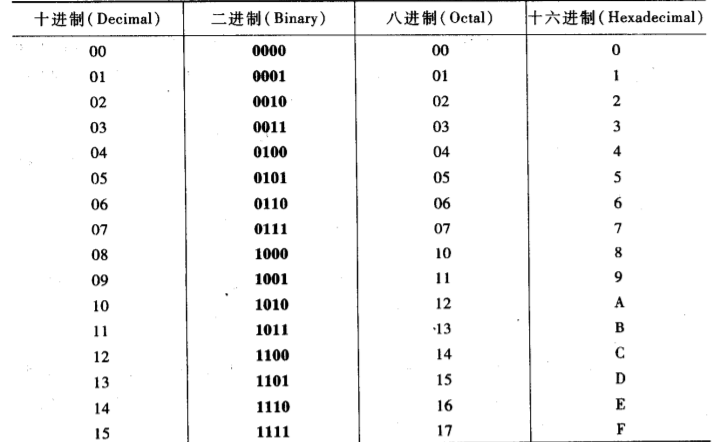
-
实际上可以有任意进制:
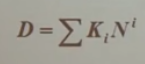
系数K、进制数N、位数i
K的取值范围在(0~N-1)
i在整数位从大数取到0,小数位从-1开始取 -
进制转换
| 转换进制 | 转换方法 | 转换进制 | 转换方法 |
|---|---|---|---|
| 二 ~ 十 | 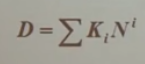 (乘法) (乘法) | 十 ~ 二 | 整数除法取余,小数乘2取整 |
| 十六 ~ 十 | 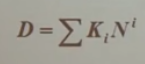 (乘法) (乘法) | 十 ~ 十六 | 二进制做桥梁 |
| 八 ~ 十 | 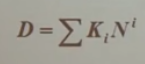 (乘法) (乘法) | 十 ~ 八 | 二进制做桥梁 |
| 二 ~ 十六 | 从低到高,四位取数,不够补零 | 十六 ~ 二 | 直接转换 |
| 二 ~ 八 | 从低到高,三位取数,不够补零 | 八 ~ 二 | 直接转换 |
| 八 ~ 十六 | 二进制做桥梁 | 十六 ~ 八 | 二进制做桥梁 |
进制转换例题

整数判断顺序:商的0可以无限除2,得0。而0放在整数前无影响,故从下往上取。
小数判断顺序:积的小数部分的0可以无限乘2,得0。而0放在小数后无影响,故从上往下取。
二进制原码、反码、补码
-
原码: 第一位符号位;其他位为数值位(1负0正)
-
正数:原码、反码、补码 都一致 -
负数:反码是 “符号位为1,数值位按位取反”;补码是反码末尾+1” -
0的反码有:+0:0 000; -0:1 111
0的补码只有一个,即(0000 0000)₂ -
补码举例:

-
二进制数的补码取值范围具有不对称性(因为0的存在)

| 四位二进制 | 表达数的二进制范围 | 十进制范围 | 个数 |
|---|---|---|---|
| 有符号数(补码) | [1000,0111] | [-8,7] | 16 |
| 无符号数 | [1111,0000] | [0,16] | 16 |
二进制算数运算
- 补码运算
因为补码运算时,符号位最后舍去,所以一定不会溢出
计算步骤:
判断参与运算的数的二进制的取位范围(加上符号位)
①写出原码(十进制~二进制)
②转换为补码进行计算(转换时,符号位不变)
③计算结果再转为原码(用补码计算出的结果仍是补码)
结果为正数:正数原码与补码相同
结果为负数:负数补码的补码是原码
(若题目中要求计算结果为绝对值,则需要去掉原码的符号位)


常用编码
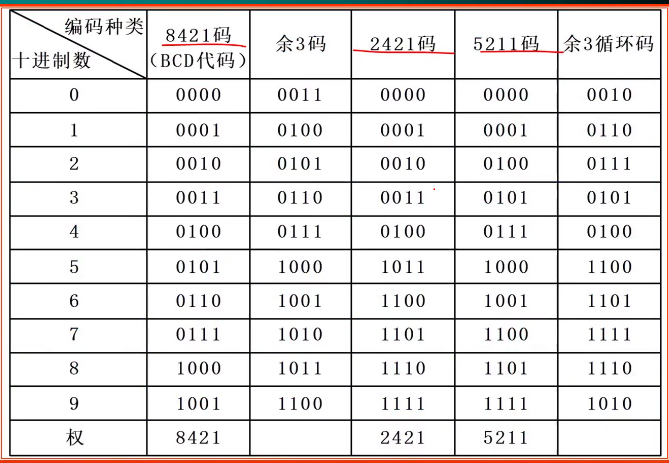
- 十进制代码
- 8421码,每四位对应一个十进制数
从最低位开始四位、四位地转换(角标:8421 / BCD)
注意“8421码”与“二进制十进制转换”的区别 - 余3码,8421码加3
- 2421码,5211码,注意权值(角标:2421 ; 5211)
- 余3循环码,每相邻两位之间只有一位不同
- 8421码,每四位对应一个十进制数

- 二进制编码
1.自然码:有权码
2.循环码(格雷码):无权码
每一位的状态变化都按一定的顺序循环
特点优势:相邻编码间只有一位变化,代码转换之间就不会产生过渡“噪声”,抗干扰能力强 - 美国标信息交换标准代码(ASCII码)
这篇关于数字电子技术(一)数制和码制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






