本文主要是介绍通过 Hilbert 变换实现单边带调制,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
简介
双边带调制
单边带调制
理想的 Hilbert 变换
频谱移位器
SSB 调制的高效实现
总结
该例子说明如何使用离散 Hilbert 变换来实现单边带调制。Hilbert 变换可应用于调制器和解调器、语音处理、医学成像、波达方向 (DOA) 测量,以及任何简化设计的复信号(正交)处理。
简介
单边带调制 (SSB) 是幅值调制 (AM) 的一种高效形式,它使用 AM 所用带宽的一半。这种方法在电话、HAM 无线电和 HF 通信(即基于语音的通信)等应用中最受欢迎。此示例说明如何使用 Hilbert 变换器实现 SSB 调制。
为了说明 SSB 调制中为何需要使用 Hilbert 变换器,我们最好先快速回顾一下双边带调制。
双边带调制
AM 的一种简单形式是双边带 (DSB) 调制,它通常由载波频率任一侧的调制信号的两个频移副本组成。更准确地说,这称为一个 DSB 抑制载波,定义为
![]()
其中 m(n) 通常称为消息信号,而 f 0 是载波频率。如上面的方程所示,DSB 调制包括将消息信号 m(n) 乘以载波 cos(2πf0n/fs),因此,我们可以使用傅里叶变换的调制定理来计算 f(n) 的变换
![]()
其中 M(f) 是 m(n) 的离散时间傅里叶变换 (DTFT)。如果消息信号是带宽为 W 的低通信号,则 F(f) 是具有两倍带宽的带通信号。让我们来查看 DSB 信号及其频谱的示例。
% Define and plot a message signal which contains three tones at 500, 600,
% and 700 Hz with varying amplitudes.
Fs = 10e3;
t = 0:1/Fs:0.1-1/Fs;
m = sin(2*pi*500*t) + 0.5*sin(2*pi*600*t) + 2*sin(2*pi*700*t);
plot(t,m)grid
xlabel('Time')
ylabel('Amplitude')
title('Message Signal m(n)')如图所示:
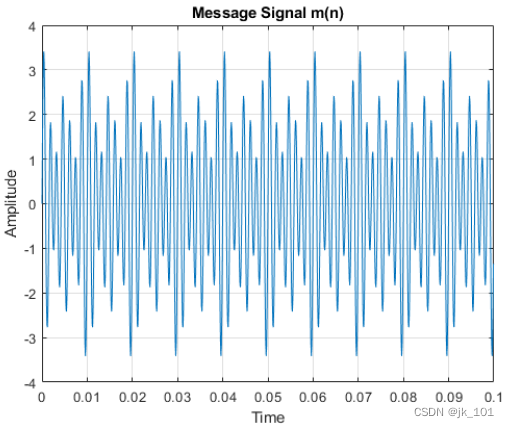
下面我们计算并绘制消息信号的功率谱。
periodogram(m,[],4096,Fs,'power','centered')
ylim([-75 12])如图所示:
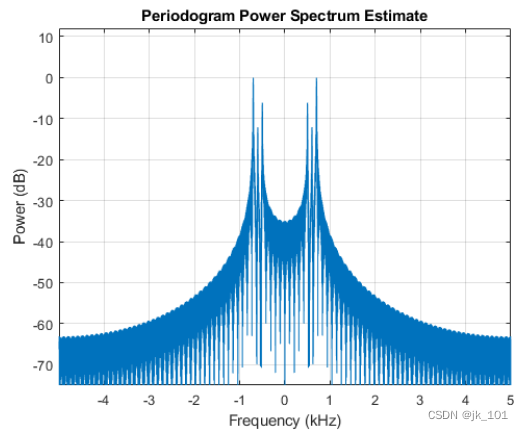
双侧功率谱清楚地显示 DC 附近的三个音调。如果我们进一步放大,就能读出每个分量的功率。
xlim([0.1 1])
ylim([-18 2])如图所示:

500 Hz 音调的功率大约为 –6 dB,600 Hz 音调的功率为 –12 dB,700 Hz 音调的功率为 0 dB,分别对应于消息信号的音调幅值 1、0.5 和 2。使用此消息信号 m(n),让我们将它乘以载波来产生 DSB 信号,并查看其频谱。
fo = 3.5e3; % Carrier frequency in Hz
f = m.*cos(2*pi*fo*t);
idx = 100;
plot(t(1:idx),f(1:idx),t(1:idx),m(1:idx),':')
gridxlabel('Time')
ylabel('Amplitude')
title('Message Signal and Message Signal Modulated')
legend('Modulated Message Signal','Message Signal m(n)')如图所示:

蓝色实线是调制的消息信号,红色虚线是缓慢变化的消息信号。在这种情况下,我们调制信号的功率谱是
periodogram(f,[],4096,Fs,'power','centered')
ylim([-75 0])如图所示:

我们可以看到,消息信号(三个音调)已移位到中心频率 f0。此外,因为幅值减半,每个分量的功率已降至四分之一,如调制后的 m(n) 的 DTFT 所示。让我们放大以查看新功率值
ylim([-20 0])如图所示:
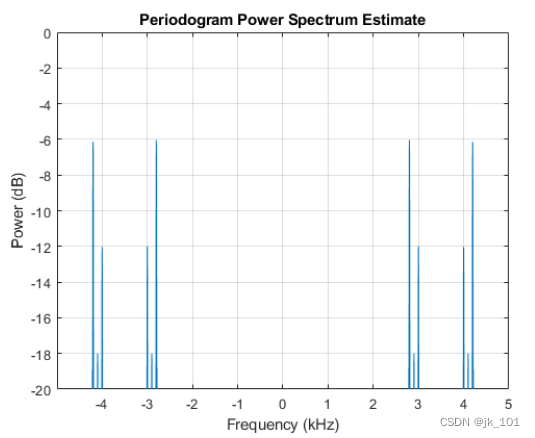
我们的正频率分量现在为 –6 dB、–18 dB 和 –12 dB。现在我们已定义 DSB 调制,接下来查看单边带调制。
单边带调制
单边带 (SSB) 调制类似于DSB调制,但它不使用整个频谱,而是使用滤波器来选择下边带或上边带。下边带或上边带的选择分别产生下边带 (LSB) 或上边带 (USB) 调制。有两种方法可以消除其中一个边带,一种是滤波器方法,另一种是定相方法。由于需要严格的滤波器,对上边带或下边带进行选择性滤波的过程很困难,尤其是当信号内容接近DC时。此示例说明如何使用定相方法,该方法使用Hilbert变换器来实现SSB调制。
SSB 调制要求将消息信号移位到另一个中心频率,而不像 DSB 调制那样产生成对的频率分量 X(f−f0) 和 X(f+f0),即避免对上边带或下边带进行滤波。这可以通过使用 Hilbert 变换器来实现。
在讨论理想的 Hilbert 变换在 SSB 调制中的应用之前,让我们先回顾一下其定义和属性。这将有助于理解其在SSB调制中的应用。
理想的 Hilbert 变换
离散Hilbert变换过程是指将信号的负频率相位提前90度,正频率相位延后90度。对 Hilbert 变换的结果进行移位 (+j) 并将其添加到原始信号会产生下文所示的复信号。
如果![]() 是
是 ![]() 的 Hilbert 变换,则:
的 Hilbert 变换,则:
![]()
是一种称为解析信号的复信号。下图显示通过理想的 Hilbert 变换生成的解析信号。

解析信号的一个重要特征是其频谱内容位于正奈奎斯特区间中。这是因为如果我们将解析信号(复信号)的虚部移位90度 (+j) 并将其加到实部,则负频率将抵消,而正频率将增加。这会产生没有负频率的信号。此外,复信号中频率分量的幅值是实信号中频率分量的幅值的两倍。这类似于单侧频谱,它包含正频率的总信号功率。
接下来我们介绍频谱位移器。频谱移位器通过调制基于我们要移动其频谱的信号形成的解析信号来对信号的频谱内容进行移位(平移)。此概念可用于SSB调制,如下文所示。
频谱移位器
使用上面定义的消息信号m(n),我们将通过 Hilbert 变换创建一个解析信号,然后将其调制到所需的中心频率。方案如下图中所示。

使用这种频谱移位方法将确保我们信号的功率移至感兴趣的频率,同时最终保持实数值信号。
如前所述,解析信号由原始实数值信号加上该实信号的Hilbert变换组成。通过Signal Processing Toolbox™中的Hilbert函数运行实信号将产生解析信号。
注意:Hilbert 函数产生完整的解析信号(复信号),而不仅仅是虚部。
mc = hilbert(m);我们还可以计算并绘制基于我们的消息信号 m(n) 构造的解析信号的频谱内容。
periodogram(mc,[],4096,Fs,'power','centered')
ylim([-75 6])如图所示:

如频谱图所示,我们的解析信号是复信号,但仅包含正频率分量。此外,如果我们测量功率,或在正频率分量上进一步放大图,我们将看到解析信号的频率分量的功率是实信号的正(或负)频率分量的总功率的两倍,即它类似于包含信号总功率的单侧频谱。请查看以下经过放大的图。
xlim([0.1 1])
ylim([-10 6])如图所示:

我们看到解析信号(复信号)的频率分量 500 Hz、600 Hz 和 700 Hz 的功率分别约为 0、–6 dB 和 6dB,这是原始信号的总功率。这些值对应于我们的原始实数值信号,它有三个音调,幅值分别为 1、0.5 和 2。
在这里,我们可以调制解析信号,将频谱内容移至另一个中心频率而不产生频率分量对组,并保持实数值信号。
为了将信号调制到载波频率 f0,我们将解析信号乘以一个指数。
mcm = mc.*exp(1i*2*pi*fo*t);如频谱移位器图中所示,调制信号后,我们将计算实部。其频谱是
periodogram(real(mcm),[],4096,Fs,'power','centered')
ylim([-75 0])如图所示:

如上图所示,我们的信号已调制到新中心频率 f0,但没有创建频率对组,即它产生了上边带。
如果我们将上面的频谱图与 DSB 调制进行比较,我们可以看到频谱移位器完成了 SSB 调制。
SSB 调制的高效实现
从前面的推论中,我们可以看出 SSB 调制信号 f(n) 可以写为
![]()
其中![]() 是解析信号,定义为
是解析信号,定义为
![]()
展开此方程并提取实部,我们得到
![]()
这会产生一个单一上边带 (SSBU)。同样,我们可以通过以下方式定义 SSB 下边带 (SSBL)
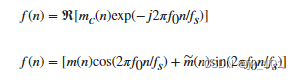
上面的 SSBU 方程提出了一种更高效的实现 SSB 的方法。该方法并不执行![]() 与
与![]() 的复数乘法,然后舍弃虚部;而是通过实现如下所示的 SSBU 只计算所需的量。如下图所示:
的复数乘法,然后舍弃虚部;而是通过实现如下所示的 SSBU 只计算所需的量。如下图所示:

为了实现上面所示的 SSB 调制,我们需要计算消息信号 m(n) 的 Hilbert 变换,并调制两个信号。但在此之前,我们需要指出一个事实,即理想的 Hilbert 变换器是不可实现的。不过,我们可以使用已开发的逼近 Hilbert 变换器的算法,例如 Parks-McClellan FIR 滤波器设计方法。Signal Processing Toolbox™ 提供设计此类滤波器的firpm函数。此外,因为滤波器会引入延迟,我们需要通过将延迟(N/2,其中 N 是滤波器阶数)添加到乘以余弦项的信号中来补偿该延迟,如下所示。
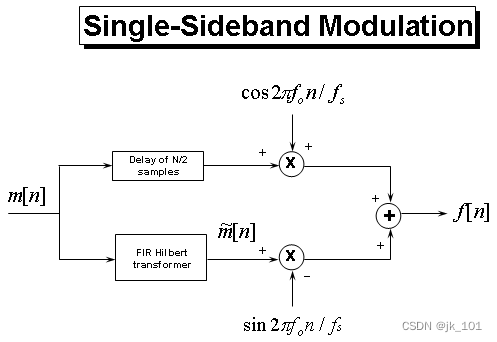
对于 FIR Hilbert 变换器,我们将使用奇数长度滤波器,它在计算上比偶数长度滤波器更高效。尽管偶数长度滤波器的通带误差较小。奇数长度滤波器能更节省计算资源,是因为这些滤波器具有几个零值系数。此外,使用奇数长度滤波器需要移位一个整数时间延迟,而偶数长度滤波器需要移位一个小数时间延迟。对于奇数长度滤波器,Hilbert 变换器的幅值响应在 w=0 和 w=π 处为零。对于偶数长度滤波器,幅值响应不必在 π 处为 0,因此它们具有更高的带宽。对于奇数长度滤波器,有用带宽限制为
![]()
让我们设计滤波器并绘制其零相位响应。
Hd = designfilt('hilbertfir','FilterOrder',60, ...'TransitionWidth',0.1,'DesignMethod','equiripple');hfv = fvtool(Hd,'MagnitudeDisplay','Zero-phase', ...'FrequencyRange','[-pi, pi)');
hfv.Color = 'white';如图所示:

为了逼近 Hilbert 变换,我们将使用滤波器对消息信号进行滤波。
m_tilde = filter(Hd,m);然后,上边带信号是
G = filtord(Hd)/2; % Filter delay
m_delayed = [zeros(1,G),m(1:end-G)];
f = m_delayed.*cos(2*pi*fo*t) - m_tilde.*sin(2*pi*fo*t);频谱是
periodogram(f,[],4096,Fs,'power','centered')
ylim([-75 0])如图所示:
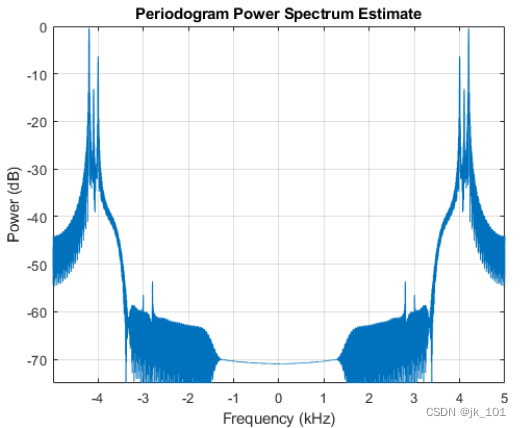
如上图所示,我们成功将消息信号(三个音调)调制到 3.5 kHz 的载波频率,并且只保留上边带。
总结
我们看到,通过使用 Hilbert 变换的逼近,我们可以产生解析信号,这在需要频谱移位的许多信号应用中很有用。具体来说,我们已看到如何使用逼近 Hilbert 变换器来实现单边带调制。
这篇关于通过 Hilbert 变换实现单边带调制的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






