BZOJ 2823 AHOI2012 信号塔 计算几何

题目大意：给定n个点(n<=50W)，求最小圆覆盖

逗我？n<=50W？最小圆覆盖？O(n^3)？

其实数据是随机生成的 经过验证 随机生成50w的点集 平均在凸包上的点在50~60个左右

于是求凸包之后就可以随便乱搞了- - 不会写O(n^3)的最小圆覆盖 写了O(n^4)的照过

注意最小圆覆盖时要讨论有两点在圆上和有三点在圆上两种情况

--------------------以上是题解-----------以下是粗口---------------------

出题人我*你*！！数据随机生成的就不能【哔】一声么！！本大爷刷这题卡了5个小时啊啊啊！

刚开始觉得做不了写了模拟退火有木有啊！！WA成狗啊有木有！！！

还有TM那坑B的样例是怎么个鬼！

void Sample_Explanation(bool f**k)

{

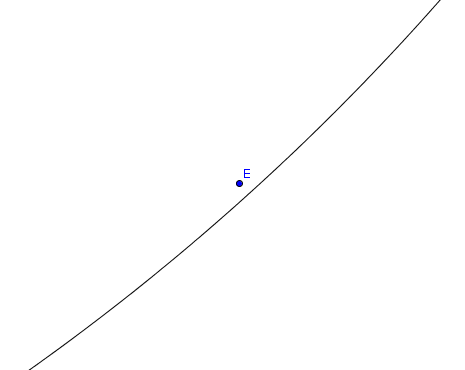
最后求得的圆是由第一个点和第三个点所构成的线段作为直径的圆

其中第五个点虽然怎么看怎么在圆上 但是这个点实际上是在圆内

如果求得答案为(2.49,2.86)，并不是被卡精度了，而是找到了由第1、3、5三个点构成的圆

显然这个圆并不是最优解

参考图片：

}

#include <cmath>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <iostream>
#include <algorithm>
#define M 500500
#define INF 1e20
#define EPS 1e-7
using namespace std;
struct point{double x,y;point(){}point(double _,double __):x(_),y(__) {}void Read(){x=rand();y=rand();}bool operator < (const point &p) const{if(fabs(x-p.x)>1e-7)return x < p.x;return y < p.y;}
}points[M],ans;
int n;
double ans_distance=INF;
point *stack[M];int top;
point *on_the_hull[M];int cnt;
double Rand()
{return rand()%10000/10000.0;
}
double Distance(const point &p1,const point &p2)
{double dx=p1.x-p2.x;double dy=p1.y-p2.y;return sqrt(dx*dx+dy*dy);
}
double Get_Slope(const point &p1,const point &p2)
{if(fabs(p1.x-p2.x)<EPS)return p1.y<p2.y?INF:-INF;return (p1.y-p2.y)/(p1.x-p2.x);
}
void Get_Convex_Hull()
{int i;sort(points+1,points+n+1);for(i=1;i<=n;i++){while(top>=2&&Get_Slope(*stack[top-1],*stack[top])<Get_Slope(*stack[top],points[i])+EPS)stack[top--]=0x0;stack[++top]=&points[i];}while(top)on_the_hull[++cnt]=stack[top],stack[top--]=0;for(i=1;i<=n;i++){while(top>=2&&Get_Slope(*stack[top-1],*stack[top])>Get_Slope(*stack[top],points[i])-EPS)stack[top--]=0x0;stack[++top]=&points[i];}for(top--;top>1;top--)on_the_hull[++cnt]=stack[top];
}
point Get_Centre(const point &a,const point &b,const point &c)
{long double a1=a.x-b.x,b1=a.y-b.y,c1=0.5*( (a.x*a.x-b.x*b.x) + (a.y*a.y-b.y*b.y) );long double a2=a.x-c.x,b2=a.y-c.y,c2=0.5*( (a.x*a.x-c.x*c.x) + (a.y*a.y-c.y*c.y) );return point( (c2*b1-c1*b2)/(a2*b1-a1*b2) , (a2*c1-a1*c2)/(a2*b1-a1*b2) );
}
void Judge(const point &p)
{int i;double max_distance=0;for(i=1;i<=cnt;i++)	{max_distance=max(max_distance,Distance(p,*on_the_hull[i]) );if(max_distance>ans_distance)return ;}ans=p;ans_distance=max_distance;
}
int main()
{srand((unsigned)time(0x0));int i,j,k;cin>>n;for(int T=1000;T;T--){top=0;cnt=0;for(i=1;i<=n;i++)points[i].Read();Get_Convex_Hull();cout<<cnt<<endl;}
}