19 捋一捋统计学里的概念

19 捋一捋统计学里的概念

标签：机器学习与数据挖掘

1.基本概念

**变异：**在自然状态下,个体间测量结果的差异称为变异（variation），变异是生物医学研究领域普遍存在的现象。严格的说，在自然状态下,任何两个患者或研究群体间都存在差异，其表现为各种生理测量值的参差不齐。
**参数估计：**指用样本指标值（统计量）估计总体指标值（参数）。参数估计有两种方法：点估计和区间估计。

2.t-检验和F-检验的差异

  T检验和F检验的关系另一种解释：
t检验有1.单样本t检验2.配对t检验3.两样本t检验。
单样本t检验：是用样本均数代表的未知总体均数和已知总体均数进行比较，来观察此组样本与总体的差异性。
配对t检验：是采用配对设计方法观察以下几种情形，1，两个同质受试对象分别接受两种不同的处理；2,同一受试对象接受两种不同的处理；3，同一受试对象处理前后。
F检验又叫方差齐性检验。在两样本t检验中要用到F检验。
回归这里采用的是单样本t-检验：

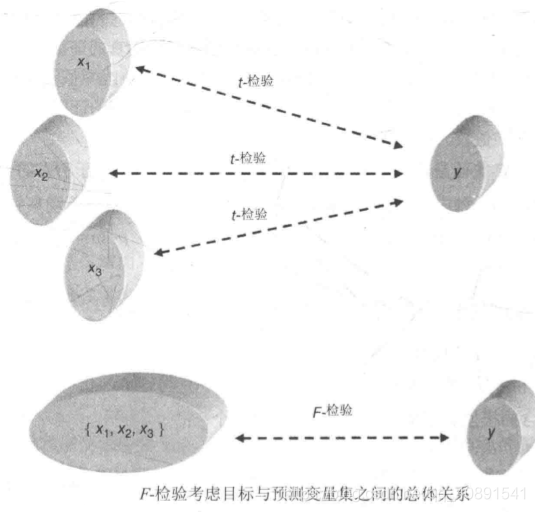
• t-检验的假设如下：
  $$\begin{array}{ll}{H}_0:& {\beta }_i=0\\ H_{\mathrm{a}}:& {\beta }_i̸=0\end{array}$$
• F-检验的假设如下：
  $$\begin{array}{l}{H}_{0^{:}}{\beta }_1={\beta }_2=\dots ={\beta }_m=0\\ H_{{\mathrm{a}}^{:}}至少存在一个{\beta }_i不等于0\end{array}$$
  **总结：**对于线性回归而言，t-检验假设是单个的分为单个自变量与因变量的检验关系。如：
  
  而F-检验 就是要么一起为0，要么一起都不为0。
  

3.t-检验 和 F-检验的用法

  t-检验过程，是对两样本均数(mean)差别的显著性进行检验。而t-检验须知道两个总体的方差(Variances)是否相等。t检验值的计算会因方差是否相等而有所不同。也就是说，t检验须视乎方差齐性(Equality of Variances)结果。所以，SPSS在进行t-test for Equality of Means的同时，也要做Levene’s Test for Equality of Variances 。
  1.在Levene’s Test for Equality of Variances一栏中 F值为2.36, Sig.为.128，表示方差齐性检验「没有显著差异」，即两方差齐(Equal Variances)，故下面t检验的结果表中要看第一排的数据，亦即方差齐的情况下的t检验的结果。
  2.在t-test for Equality of Means中，第一排(Variances=Equal)的情况：t=8.892, df=84, 2-Tail Sig=.000, Mean Difference=22.99
既然Sig=.000，亦即，两样本均数差别有显著性意义！
  3.到底看哪个Levene’s Test for Equality of Variances一栏中sig,还是看t-test for Equality of Means中那个Sig. (2-tailed)啊?
答案是：两个都要看。
先看Levene’s Test for Equality of Variances，如果方差齐性检验「没有显著差异」，即两方差齐(Equal Variances)，故接著的t检验的结果表中要看第一排的数据，亦即方差齐的情况下的t检验的结果。
反之，如果方差齐性检验「有显著差异」，即两方差不齐(Unequal Variances)，故接著的t检验的结果表中要看第二排的数据，亦即方差不齐的情况下的t检验的结果。
  简单来说就是实用T检验是有条件的，其中之一就是要符合方差齐次性，这点需要F检验来验证。
此段来自：T检验与F检验的区别_____f检验和t检验的关系（这博客说的很好啊！）

4.贝索校正

贝索校正的原理是：用以上定义的样本变异量来估计母体变异量时，平均来说不会有偏差。如果我们用「≈」代表「平均来说」，我们可以用下式来表示这个陈述：
$$\frac{{\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}{n-1}\approx \frac{{\sum }_{i=1}^n{\left(x_i-\mu \right)}^2}{n}$$

强烈推荐：关于统计学中的N-1（这老师也写得非常不错。）