百囚犯问题的拓展思考

前两天在B站刷视频，刷到了百囚犯问题的视频详解，该问题由丹麦计算机科学家Peter Bro Miltersen于2003年首次提出，是经典的概率论和组合数学问题。在理解这题的思路之余，我又产生了一些新的思考。

问题描述

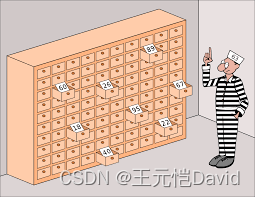
在监狱中有100名囚犯，编号为1-100号。典狱长决定给囚犯们一次特赦的机会，条件是通过一项挑战。在一个房间中放着一个有100个抽屉的橱柜，里面随机放着与囚犯编号对应的1-100的号码牌。挑战开始后，每个囚犯依次进入该房间，打开不超过半数的抽屉，并从中找到与自己对应的号码则为成功，每名囚犯出去时该橱柜恢复原样。从第一名囚犯进入直至最后一名囚犯出来期间不允许有任何交流，任何一名囚犯挑战失败都会导致所有囚犯挑战失败，只有全部成功才能够特赦该100名囚犯。如果囚犯们都随机打开50个抽屉，他们的特赦几率微乎其微。所以囚犯们需要在开始之前讨论出一个最佳策略，来提高整体特赦的概率。

我们知道，如果每个囚犯都完全随机选择的话，则特赦概率为 0.5^100 ≈ 8*10^-31，但问题的提出者给出，存在一种简单可执行的方案，能将特赦概率提升到 0.3（30%）以上，没看过这个问题的不妨思考一下。

最佳策略

问题的提出者一开始也没想到更好的策略，在同事的提醒之下，他想到了利用环来解决这个问题。如果你之前接触过算法，简单来说，就是把100个抽屉和其中的纸条，看成一个有向有环图，此题即可抽象为有向有环图中不存在大于 100÷2=50 长度环的概率，计算得知约为 0.311828。

有大量的解释举证珠玉在前，本文不准备展开介绍具体策略和证明过程，有兴趣的朋友可以参考下面的文章：

https://www.bilibili.com/video/BV1kt4y1t75F b站视频

https://zhuanlan.zhihu.com/p/31211827 知乎专栏

https://blog.csdn.net/qq_36721220/article/details/105580441 CSDN 解释及代码模拟

进一步思考

即使是上述的最佳策略，对于单个囚犯而言，成功的概率依然是 0.5，并没有因为策略而提高，策略只是极大幅度提高了整体的成功概率。更进一步来说，策略将一百个独立随机事件转变成了互相影响的非独立随机事件。

对于这个问题还有哪些可执行的策略呢？他们分别是如何影响最终整体的成功概率的？为了这个问题我彻夜难免，想出来如下几点。

策略1. 全部做同样的选择

如果从一开始决定，每个人都选择同样的50个抽屉，例如编号1到50号，则最后整体成功的概率显然为 0，但对于单个人而言，成功的概率依然为 0.5。

策略2. 均分成两个团队，分别做同样的选择

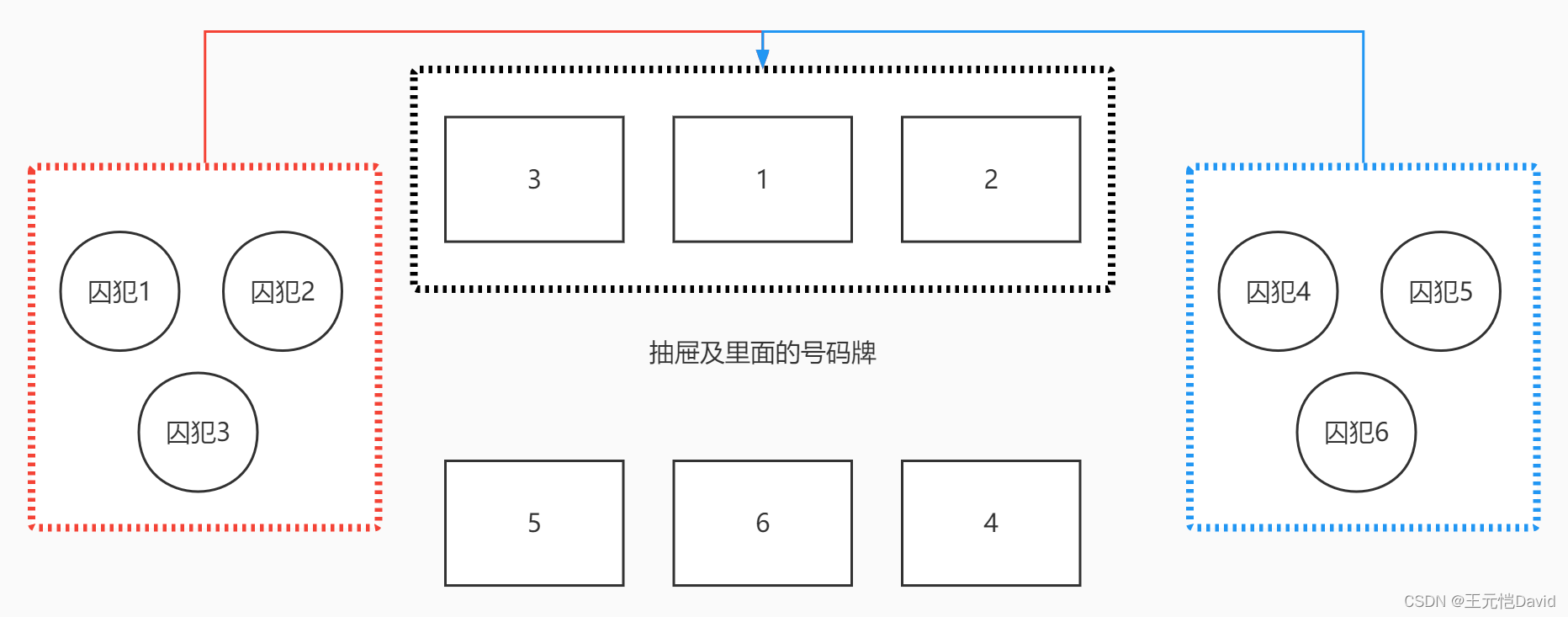
如果从一开始决定，将100人均分成两个团队各50人，其中一个团队每个人都选择同样的50个抽屉，例如编号1到50号，另外一个团队每个人都选择剩下来的同样50个抽屉，例如编号51到100号，那最后整体成功的概率是多少呢？显然它是大于0的。

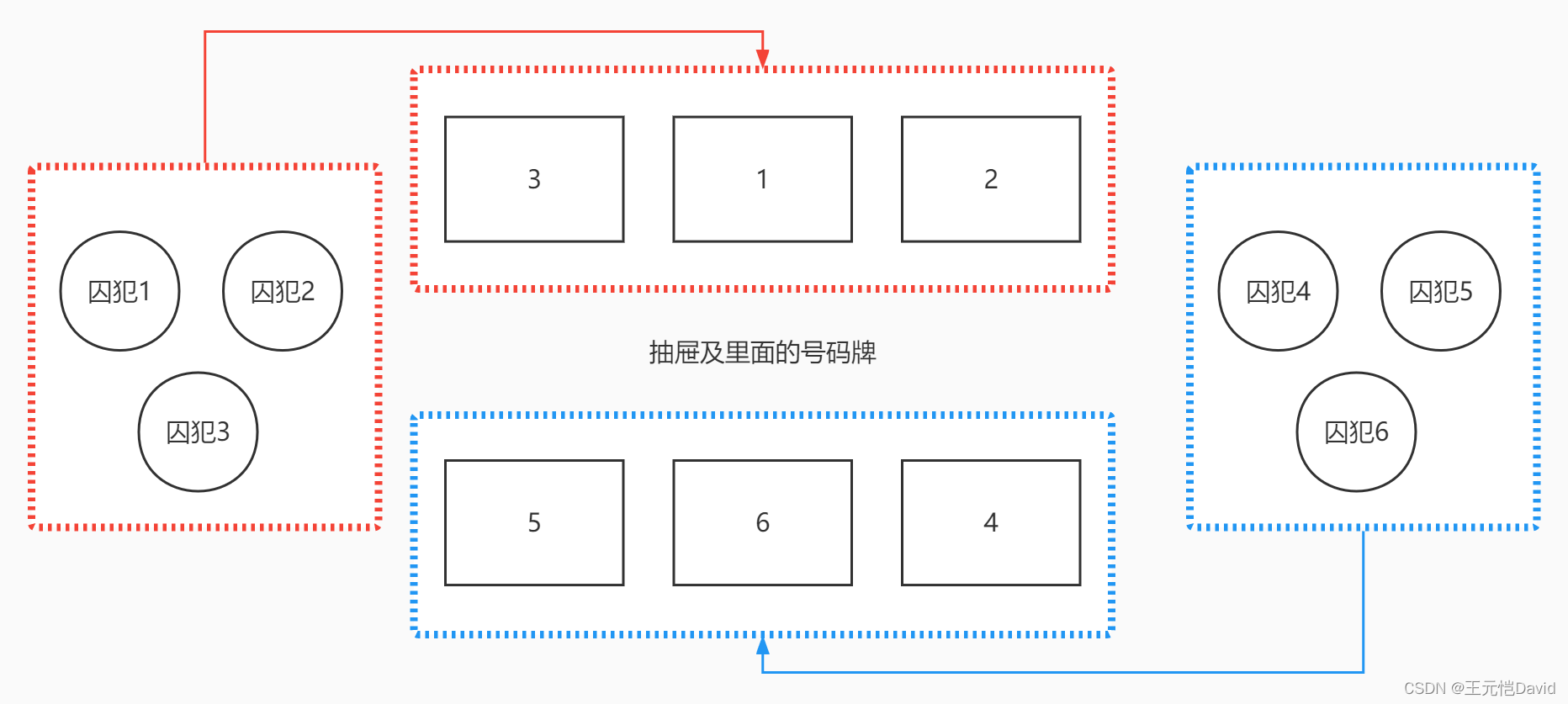
我们计算一下，先算100个号码牌放入100个抽屉的可能性总数。打开第一个抽屉，我们手中还剩100个号码牌，选一个放入，有100个可能性；打开第二个抽屉，我们手中还剩99个号码牌，选一个放入，有99个可能性……以此类推，最后一个抽屉，我们手中只剩最后一个号码牌，没得选，有1个可能性，所以可能性总数为100×99×98×……×1=100!

那，50人的团队都成功的可能性总数是多少呢？我们看第一个团队，编号1到50号（这里的编号是一一对应的，所以51到100号的可能性完全相同），他们都选择打开1到50号抽屉。也就是说，想要成功，1到50号抽屉里，必须恰好放着1到50号的号码牌，顺序可以完全打乱。1号抽屉可以放1到50号，即50个可能性；2号抽屉可以放1到50号，但由于1号已经放入一个号码牌了，所以只有49个可能性……以此类推，所以只看前50个抽屉都成功的可能性为50×49×48×……×1=50! 。如果第一个团队都成功了，那第二个团队一定能都成功（因为第一个团队在前50个格子已经把号码牌“消耗”掉了）。剩余从51号抽屉到100号抽屉，同理也是 50! 的可能性，所有人都成功的可能性总数为 50!×50! 。

最后成功率为 50!×50!÷100!，结果约为 9.91E-30，大概是纯随机成功的12倍，但对于单个人而言，成功的概率依然为 0.5。值得一提的是，虽然阶乘的增长倍率大于次方增长倍率，但这个式子在算到8000人后，还是大于纯随机，倍率一直在100倍之内浮动。随之产生一个猜想，这个策略的成功率恒大于随机策略吗？

即求证如下数学式子：

$$\frac{x!\times x!}{(2x)!}>\frac{1}{2^{2x}}(x\ge 1)$$

数学归纳法证明如下：

1. 验证等于1时式子成立：$$\frac{1!\times 1!}{(2)!}=\frac{1}{2}>\frac{1}{2^2}=\frac{1}{4}$$
2. 假设 $x=n$ 时成立，即 $$\frac{n!\times n!}{(2n)!}>\frac{1}{2^{2n}}(n\ge 1)$$
3. 求证 $$\frac{(n+1)!\times (n+1)!}{(2n+2)!}>\frac{1}{2^{2n+2}}(n\ge 1)$$
4. 化简
   $$\frac{(n+1)!\times (n+1)!}{(2n+2)!}=\frac{n!\times n!\times (n+1)\times (n+1)}{(2n)!\times (2n+2)\times (2n+1)}=\frac{n!\times n!}{(2n)!}\times \frac{n+1}{2n+2}\times \frac{n+1}{2n+1}$$

根据2假设中的大于关系

$$\frac{n!\times n!}{(2n)!}\times \frac{n+1}{2n+2}\times \frac{n+1}{2n+1}>\frac{1}{2^{2n}}\times \frac{n+1}{2n+2}\times \frac{n+1}{2n+1}=\frac{1}{2^{2n}}\times \frac{1}{2}\times \frac{n+1}{2n+1}$$

$$\frac{1}{2^{2n}}\times \frac{1}{2}\times \frac{n+1}{2n+1}>\frac{1}{2^{2n}}\times \frac{1}{2}\times \frac{n+1}{2n+2}=\frac{1}{2^{2n}}\times \frac{1}{2}\times \frac{1}{2}=\frac{1}{2^{2n+2}}$$

得证。

再进一步，我们继续求 $$f(x)=\frac{x!\times x!}{(2x)!}(x\ge 1)$$

根据上面的过程，有

$$f(x+1)=f(x)\times \frac{1}{2}\times \frac{x+1}{2x+1}=f(x-1)\times \frac{1}{2^2}\times \frac{x+1}{2x+1}\times \frac{x}{2x-1}=\dots \dots$$

$$=f(1)\times \frac{1}{2^x}\times \prod _{i=1}^x\frac{i+1}{2i+1}=f(1)\times \prod _{i=1}^x\frac{i+1}{2\times (2i+1)}=\frac{1}{2}\times \prod _{i=1}^x\frac{i+1}{4i+2}=\prod _{i=0}^x\frac{i+1}{4i+2}$$

即

$$①\frac{x!\times x!}{(2x)!}=\prod _{i=1}^x\frac{i}{4i-2}(x\ge 1)$$

又有阶乘展开

$$②\frac{x!\times x!}{(2x)!}=\prod _{i=1}^x\frac{i\times i}{i\times (x+i)}=\prod _{i=1}^x\frac{i}{x+i}(x\ge 1)$$

①②联立得

$$\prod _{i=1}^{x}4i-2=\prod _{i=1}^{x}x+i(x\ge 1)$$

得出了一个很不可思议的式子，且这个式子是能验证为正确的：

2 = 2
2 × 6 = 3 × 4
2 × 6 × 10 = 4 × 5 × 6
2 × 6 × 10 × 14 = 5 × 6 × 7 × 8

数学太美了！！！

策略3. 利用差值特性的策略

我们知道，抽屉是100个，编号1到100号，号码牌编号也是1到100号，显然如果分别求和，是相等的，如果把抽屉的编号减去抽屉里号码牌的编号（下简称差值），把这一百个差值相加的和，即是抽屉的和减去号码牌的和，结果一定为0。再根据概率分布，存在差值99的概率是最小的，-99同理，但存在差值为0的概率却很高，我们可以利用这一点做文章。

给定策略，k号囚犯先去找第k号抽屉，拿到的号码牌编号为m号，再去找 n=k+(k-m) 号抽屉，如果抽屉不存在（大于100或小于1），则取余数，如果抽屉已被翻开，则打开最相邻的抽屉。n号抽屉里号码牌编号为o，再下一个抽屉为 p=k+(n-o)。重复以上步骤直至找到号码牌k，或是翻完50个抽屉宣布失败。这个策略更复杂，执行起来也更麻烦。

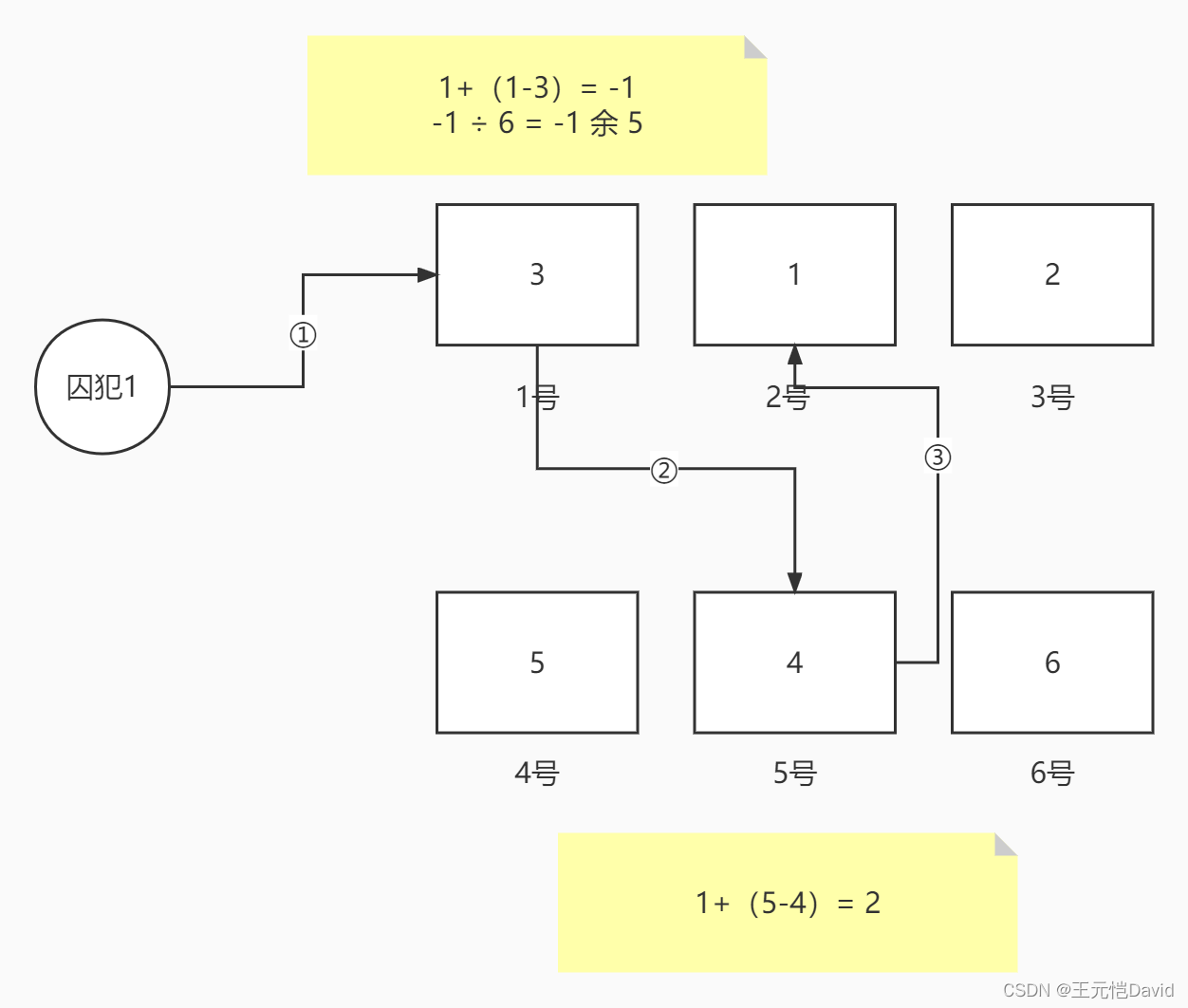
从分布规律的角度来说，整体成功的概率是要大于纯随机的，但对于单个人而言，成功的概率依然为 0.5。我没能想到严密的证明过程，更给不出概率表达式进行计算，希望有想到的朋友能提出。

数值验证

我们可以通过程序模拟这个场景进行数值验证，由于算力关系，我只模拟到最多12人的情况。

总结

我们通过思考多种方法，更深刻的理解了百囚犯问题中独立概率与非独立概率，意外之喜是发现了一个有趣的等式：

$$\prod _{i=1}^{x}4i-2=\prod _{i=1}^{x}x+i(x\ge 1)$$

由2开始公差为4的等差数列的n项乘积，等于由n+1开始的连续n个自然数的乘积。