本文主要是介绍开关电源基础05:基本开关电源电感器设计(1),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
说在开头:关于第五届索尔维会议(1)
1927年对物理学是个非常重要的年份,因为这年发生了一件非常重要的事,那就是第五届索尔维会议;后来的发展证明,它毫无疑问是有史以来最著名的一次索尔维会议。爱因斯坦、薛定谔等人都如约而至,物理学的大师们齐聚一堂,并流传下来了那张令多少后人唏嘘不已的“物理学全明星梦之队”的世纪照片;如果硬要挑点不足出来的话,那就是索末菲和约尔当不在其中。

会议从10月24日进行到29日,会议的主题本来是“电子和光子”,但大家主要的精神头都放在了量子的“不确定原理” 上,会议之前玻尔已经知道爱因斯坦反对几率的解释(会议之前爱大神写信给玻尔说了:上帝不掷骰子),他心里像是压了一块石头:那可是爱因斯坦啊,现在物理学界的霸主,要是他不同意,那就麻烦了。洛伦兹是大会主席,他和普朗克是老一代物理学家的代表;剩下的人分成了三拨:实验物理学家们关心的是做出了什么样的实验,以居里夫人为首,其他人是康普顿、布拉格、劳厄以及德拜,在这次会议上属于吃瓜群众;会议主力军是哥本哈根学派,以玻尔为大BOSS,得力干将是海森堡、泡利、玻恩、狄拉克等;剩下的就是反对派了,为首的是爱因斯坦,得力干将是德布罗意和薛定谔。好,现在先请主席发言。
洛伦兹一开始就对几率解释给批了一顿,说:电子只会在确定的时间出现在确定的地点,有人企图用可笑的几率来解释电子,那绝对是错误的。后来越来越激动:我不知道我为什么现在还活着,只遗憾自己没在5年前死去,那这些东西至少还没在我眼前出现。玻尔坐在台下脸色不怎么好,他转头看爱因斯坦,没啥表情,这下心里更不踏实了。再往后看,咦,海森堡和泡利呢?这俩小子去哪了?正想着,海森堡和泡利两个进来了,嚯,这两人胡子也没刮,头发乱糟糟的,这是被人抢劫了么?原来这两人住旅馆的时候,讨论问题太入神,没注意到小偷把它们的行李和车票都偷走了,只好当了几天盲流,好不容易来到了布鲁塞尔。好,各方主力已经集结完毕,好戏正式拉开帷幕。
第一天是实验物理学家的议题,布拉格的《X射线反射的强度》和康普顿的《辐射实验与电磁定理间的不一致》,一切非常平静。第二天,德布罗意开始发言,讲述他的导波理论;他认为粒子是波动方程的一个奇点,它必须受波的控制和引导。泡利站起来全力开火:批评了这个理论,他首先不能不能容忍历史车轮倒转回到传统,列举了一系列实验结果来反驳德布罗意;海森堡在边上也不断帮腔。德布罗意哪禁得住这俩哥们的火力啊,德布罗意最后不得不公开声明放弃他的观点。爱因斯坦还是面无表情,干看着不说话。
第三天上午,海森堡和玻恩联合发言,主要关于不确定原理、量子论的应用等;他们介绍完后,还回顾了一下量子论的的发展历程,这门学科是从普朗克、爱因斯坦、玻尔那里传承下来的的。爱因斯坦这时突然露出了笑意,旁边的埃伦斯特一看,这老头当木头人也好几天了,有问题啊。第三天下午,薛定谔作报告讲的是波动方程,顺便声援德布罗意,他刚发言完毕,台下蹭蹭站起来三个人:玻尔、玻恩、海森堡;薛定谔脑袋一懵,仿佛回到了在根本哈根的那些日子,马上就招架不住了,他期盼地盯着爱因斯坦,但大神还是一言不发,薛定谔心里不爽:您老也太淡定了吧。(参考自:吴京平-无中生有的世界)
一,电感器电流
我们在《基本开关电源拓扑》中已经介绍了基本开关电源拓扑的直流传递函数,如下图所示,这是通过伏秒平衡原理推导出来的,我们看到Vin和Vo是固定电压(平均电压)。但是在实际开关电源工作过程中(稳态时),Vin和Vo电平是完全不动的么?那显然是不对的,我们会在直流电压上叠加交流电压(纹波电压),才是完整的输出电压:Vo + Vripple。而之所以电源输出电压由这两部分叠加而成,是因为:电源输出电流是由直流电流和交流电流(纹波电流)所组成。

1,电感器电流波形中的直流分量和交流分量
从电源拓扑本身来看,最重要的电流在哪里?我相信大家只要仔细回想一遍拓扑结构,就能发现开关电源拓扑中最重要的位置在交换节点(电感器、开关管和二极管交汇点),而交换节点的电流全都通过了电感器(二极管和MOS管各自通过一半)。电感器的电流大小决定了开关电源能量传输的大小,影响了输出纹波电流的大小,决定了开关电源所占面积的大小(决定了功率器件的选型)。所以对电感器电流的分析至关重要,首先我们再来回顾一下三个基本拓扑中各电流之间的关系,如下图所示。

我们又一次需要从电感方程出发:V = L * dI/dt,可得: ΔI =ΔV*Δt/L;其中ΔV*Δt就是伏秒积,所以对于固定电感器来说,电流变化∆I![]() 就取决于伏秒积的大小;而伏秒积取决于输入/输出电压(占空比D)和开关频率(f)。所以总体来说要改变ΔI,那么必须改变:占空比D,开关频率f,或则电感器感值L。从这个公式也看出来,负载电流Io的大小与ΔI无关,但是我们在《电源变换器基础》中已知道负载电流Io与电感平均电流Idc成正比,举个栗子:BUCK拓扑的Io =Idc。如下表格所示,为电感交流电流和直流电流随L,Io,D以及开关频率f的变化。
就取决于伏秒积的大小;而伏秒积取决于输入/输出电压(占空比D)和开关频率(f)。所以总体来说要改变ΔI,那么必须改变:占空比D,开关频率f,或则电感器感值L。从这个公式也看出来,负载电流Io的大小与ΔI无关,但是我们在《电源变换器基础》中已知道负载电流Io与电感平均电流Idc成正比,举个栗子:BUCK拓扑的Io =Idc。如下表格所示,为电感交流电流和直流电流随L,Io,D以及开关频率f的变化。

从上表格中可以得到如下结论:
1. 电感值L增加:
1, Idc保持不变,因为电感直流电流取决于输出电流Io和占空比D;
——可以通过伏秒定律推导出,具体参考上面电流关系表,或则《基本开关电源拓扑》中“三种基本拓扑电流比较”章节。
2, 根据电感方程:ΔI =ΔV*Δt/L,ΔI随着L的增加而减小。
2. 输出电流Io增加:
1, 电感直流电流Idc随Io线性增加,而且在BUCK拓扑中:Idc =Io;
——BUCK拓扑输出端与电感器串联,电感电流与输出电流完全相等。
2, ΔI在理论上与Io无关,所以ΔI不随Io的变化而变化。
——接下来章节会讲到“电流纹波率”r的概念,在开关电源设计过程中,会将电感直流电流Idc与纹波电流ΔI人为关联起来,作为电源设计的初始条件(最关键的输入参数),而输出电流Io与电感直流电流Idc成正比,所以从这个角度来看,ΔI与Io是相关的。
3. 占空比D增加:
1, 对于BUCK拓扑来说,占空比D表现的是输出电压和输入电压之比:Vo/Vin,而与负载电流Io无关,所以I![]() dc与占空比D无关;(具体分析参考:《电源变换器基础》相关章节)
dc与占空比D无关;(具体分析参考:《电源变换器基础》相关章节)
2, 对于BOOST和BUCK-BOOST拓扑来说,根据伏秒定律得到Idc = Io/(1-D)(如上电流关系表所示),所以当占空比增加时,电感直流电流Idc也相应增加。
3, 对于BUCK和BUCK-BOOST拓扑来说,D增加意味着Ton=T*D增加,而Toff = 1-Ton则减减少,所以在关断阶段内的伏秒积:Voff*Toff = Vo*Toff减小,根据ΔI =ΔV*Δt/L,所以ΔI随着D的增加而减小;
4, 但对于BOOST拓扑,占空比D增加,意味着Ton增加,而D = (Vo-Vin)/Vo,则说明Vin减小,根据导通阶段内的伏秒积:Von*Ton = Vin*T*(Vo-Vin)/Vo= Vin*T *(Vo-Vin)/Vo,我们可以知道当Vin = 0或则Vin=Vo时为0,当Vin =Vo/2时伏秒积达到最大,即当D = 0.5时ΔI达到最大值。
——所以从整体来描述BOOST拓扑ΔI随占空比D的变化:D从0到0.5时ΔI从0抛物线上升到最大值,D从0.5到1时ΔI从最大值抛物线下降至0。
4. 开关频率f增加:
1, Idc与负载电流Io成正比(BOOST和BUCK-BOOST拓扑也与D有关),而负载电流的大小取决于负载所需电流大小,与开关频率无关;
2, 根据电感公式ΔI =ΔV*Δt/L,由于Δt随着f线性减小,所以ΔI也随f线性减小。
5. 现在我们梳理一下我们分析得到的结论:
1, 改变电感值L不会影响Idc,但会影响ΔI(反向线性关系),如下左图所示;
2, 改变开关频率f不会影响Idc,但会影响ΔI(正向线性关系),如下左图所示;
3, 改变占空比D,在BOOST和BUCK-BOOST拓扑上会影响Idc,同时也会影响所有拓扑的ΔI(不同拓扑影响不同);
4, 如果D和Io不变,那么Idc将固定不变。

电感器电流(包括直流和交流)随不同因素的变化趋势,对开关电源的设计方向非常重要。我们能够知晓所做选择带来的好处与坏处,比对与产品整体设计方向是否一致。
2. 交流电流、直流电流及峰值电流
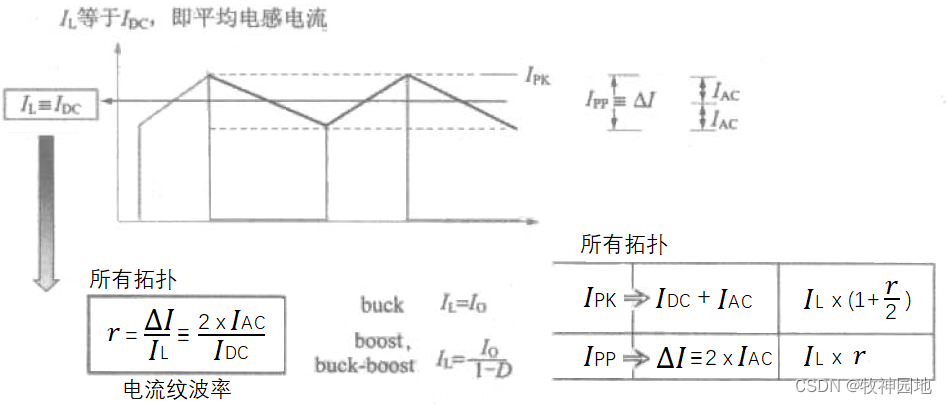
如下图所示为滤波电感器的:直流电流Idc、交流电流Iac、峰峰值电流Ipp=ΔI,以及峰值电流Ipk;我们定义:交流电流Iac=ΔI/2,电流纹波率为r = ΔI//IL = 2*Iac/Idc;假设BUCK拓扑的电流纹波率r=0.4,电源负载电流为1A,那么Idc = IL = 1A,电流峰峰值Ipp = ΔI = 1*0.4 = 0.4A,峰值电流Ipk = 1+0.2 = 1.2A。假设是BOOST/BUCK-BOOST拓扑,电流纹波率是0.4,负载电流是1A,D = 0.5,那么Idc = Io/(1-D) = 2A,电流峰峰值Ipp = ΔI = 2*0.4 = 0.8A,峰值电流Ipk = 2+0.4 = 2.4A。
——我们需要注意的是:电流纹波率定义的是电感电流的峰峰值电流与直流电流之比,而非电源输出电流;对于BOOST和BUCK-BOOST拓扑来说,输出电流与电感电流并非相等。
1. 电感器的直流电流分量很大程度上决定了绕组铜线的损耗:I²dc*Rdc;但实际上电感器的损耗还受到磁芯损耗的影响,其只与电感器交流电流分量(ΔI)决定,而与直流分量(Idc)无关。(具体原理参考:《电感器原理》相关章节)
——如果绕组铜线直径选择有问题,由于趋肤效应会导致交流电阻Rac很大,从而导致交流损耗增加。
1, 在开关电源拓扑中,在稳态时输出滤波电容器的平均电流是0(每一开关周期的输入、输出电流相等),直流电流与输出滤波电容器无关。
——输出滤波电容器与纹波电流相关,纹波电流通过滤波电容器回流,所以滤波电容器的ESR对电源纹波电压非常重要:Vripple = ΔI*ESR。
2. 电感器的峰值电流同样也是开关管和二极管(同步拓扑中是MOS管)的峰值电流,所以峰值电流是所有电流分量中最重要的,需要特别关注:
1, 不能超过开关管和二极管的额定电流,会导致击穿损坏;
2, 是功率器件长期热积累和温升的源头;
3, 电感器磁芯的磁场强度与电流大小成正比,电流峰值时电感器磁场强度达到最大值,不能导致电感器磁芯饱和,否则电感器短路导致开关管损坏。
3. 交流电流:Iac= ΔI/2,由电感公式可得:2*Iac = ΔI =ΔI*Δt/L,所以电感峰峰值电流Ipp = ΔI可以看成单位电感值上的伏秒积,即:伏秒数减小一半则峰峰值电流(交流电流)减小一半,电感值增加一倍则峰峰值电流(交流电流)减小一半;
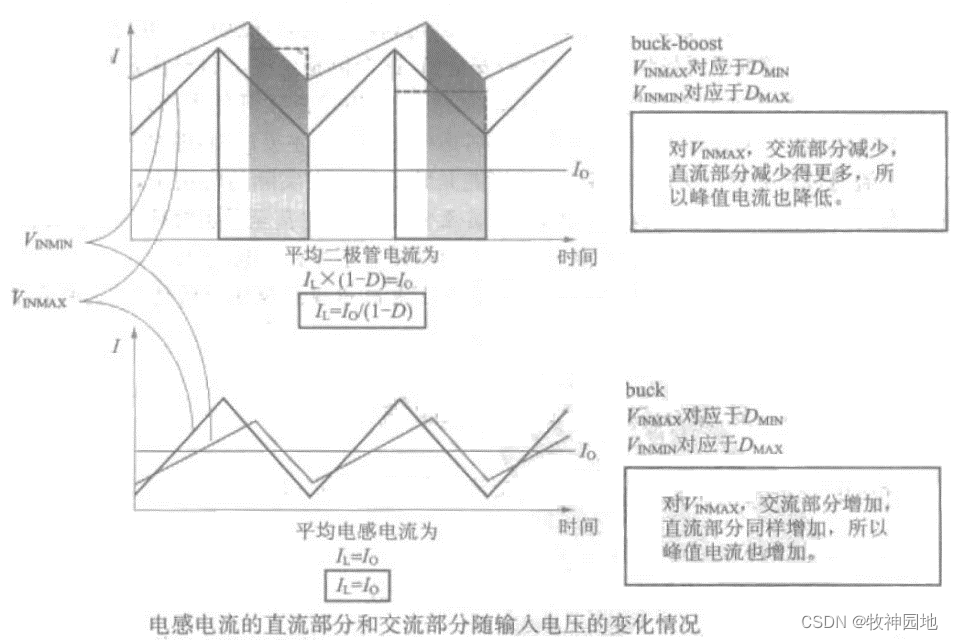
4. 对于所有拓扑来说,大占空比对应低输入电压(VINmin),小占空比对应高输入电压(VINmax);因此在任何情况下增加占空比D意味着输入电压(幅值)的降低;所以对于BOOST和BUCK-BOOST拓扑电源来说,如果输入输出电压比很大,那么电感器的直流分量也会很小:I![]() L = Io/(1-D),如下图所示。
L = Io/(1-D),如下图所示。
3. 电流纹波率r
3.1 基本概念
我们从上面对电感器电流分析的例子中已经看到,电流纹波率r是非常关键的一个参数,它将原本相互独立的电流分量:Idc和ΔI关联了起来;可以通过负载电流Io推导出电感器所有电流分量,进一步推导出拓扑中所有器件(包括:开关管、二极管、输入电容器及输出电容器)上的电流分量,从而可以确定电源拓扑中所有器件的选型。r值一般选择0.3~0.5之间,跟电源拓扑、开关频率、以及特定工作环境都无关;几乎所有的开关电源设计都是从设置r开始的。
电流纹波率r =ΔI/IL = 2*Iac/Idc,它是电感器电流的交流分量和直流分量的比值。一旦确定了r则确定了开关电源拓扑中所有器件的参数,因此r值的选择将影响开关电源器件的选择,决定开关电源的成本。电流纹波率r仅适用于连续导通模式,其有效范围是0~2:当r = 0时,则Iac![]() =0,此时根据电感公式ΔI = ΔV*Δt/L可得L必须使无穷大(所以r = 0并不实用);若r = 2时,则电源处于临界连续导通模式,由定义可知此时Iac = Idc。
=0,此时根据电感公式ΔI = ΔV*Δt/L可得L必须使无穷大(所以r = 0并不实用);若r = 2时,则电源处于临界连续导通模式,由定义可知此时Iac = Idc。
——当然如果是同步开关拓扑,电源可以工作在强迫连续导通模式,r也可以大于2。

根据电感公式:ΔI = ΔV*Δt/Luh,其中Et = ΔV*Δt,表示伏微秒数,L![]() uh表示以uH为单位的电感量,如此方便计算;那么我们可得:r = ΔI/Idc = Et/(Luh*Idc) = (Von*D)/[(Luh*Idc)*f] = Voff*(1-D)/ [(Luh*Idc)*f];那么我们从公式反推得到L
uh表示以uH为单位的电感量,如此方便计算;那么我们可得:r = ΔI/Idc = Et/(Luh*Idc) = (Von*D)/[(Luh*Idc)*f] = Voff*(1-D)/ [(Luh*Idc)*f];那么我们从公式反推得到L![]() uh = Von*D/(r*Idc*f)。
uh = Von*D/(r*Idc*f)。
——我们在确定输入电源电压(Vin),输出电源电压(Vo)和电流(Io)后可以确定Von和占空比D;再确定了开关频率f![]() 和电流纹波率r后,就能计算出电感值L
和电流纹波率r后,就能计算出电感值L![]() uh;再结合由r确定的电感峰值电流大小,计算得电感器额定电流值,这样就能确定电感器的选型。
uh;再结合由r确定的电感峰值电流大小,计算得电感器额定电流值,这样就能确定电感器的选型。
3.2 r值的选择
好,现在的关键问题在于我们怎么确定r值呢?一开始我们就说了r值应该选择在0.3~0.5之间,根据实际研究表明:综合考虑拓扑个参数应力(电压、电流应力)以及电源面积,r选择0.4为最优。我们从如下几个方面考虑:
1. 电感器尺寸:一般电感器尺寸与其能量处理能力成正比,即,输出功率越大就需要更大体积的磁芯;磁芯的最大能量储存能力要大于E = 1/2*L*I²pk,否则电感将饱和(电感饱和的后果,咱们应该写过18遍了,哈哈);
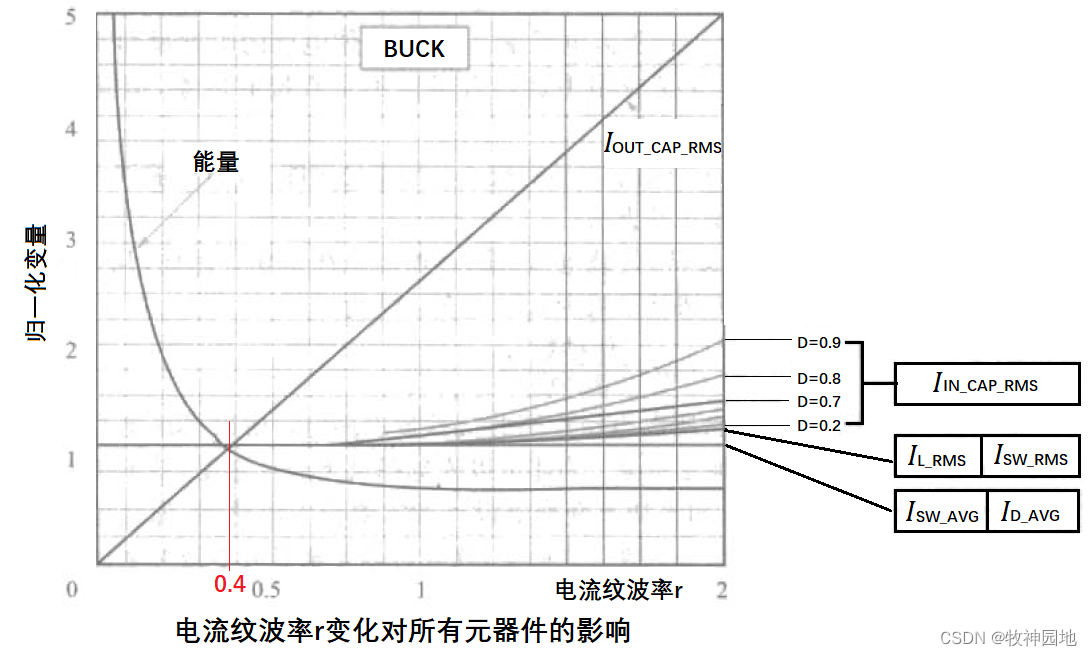
2. 如下图为电感器处理能量E = 1/2*L*I²pk与r的曲线,可以看到在r=0.4附近有一个拐点:当r < 0.4越多则需要电感器尺寸就越大,相反当r>0.4则电感器尺寸变化相对没那么大;
3. 如下图也描绘了BUCK拓扑输出电容器电流(有效值电流:I![]() OUT_CAP_RMS)随r变化的曲线,我们可以看到输出电容器电流随r线性增加,当r > 0.4后电容电流增加很大,会导致电容器内部大量发热(电解电容器ESR较大);
OUT_CAP_RMS)随r变化的曲线,我们可以看到输出电容器电流随r线性增加,当r > 0.4后电容电流增加很大,会导致电容器内部大量发热(电解电容器ESR较大);
——输出电容器采用陶瓷电容的话,由于ESR非常小,可以容许较大的r值。
4. 从下图也可以看到:开关管(上管MOS管)、二极管(下管MOS管)和电感器的电流有效值和平均值随r的变化较小,所以与输出电容器不同,这些功率器件损耗受r的影响较小。
5. 下图虽然以BUCK拓扑为例,但这个图也对所有拓扑都适用,除了电容电流曲线不同拓扑会有差别。
3.3 r值的限制
1. 一般开关电源芯片会有电流限制范围,如果电流限制过低则r值无法设置成最优值。举个栗子:如下图所示LM2673(BUCK)电流限制最小值为5.3A(超过该值可能发生保护动作),所以我们需要保证在实际正常工作中电流峰值不会达到该值。

如果我们要实现5A的输出电流,r值取0.4,那么峰值电流Ipk = Io + Iac = Io*(1+r/2) = 6A > 5.3A;如果按照5.3A峰值电流来反推r < 2*((5.3/5) - 1) = 0.12;此时电感器能量处理能力(电感器尺寸)大概是r=0.4时的3倍。
如果电流限制可以通过电流限制电阻值调的更高,那么需要计算其相应的电流限制的大小,使得r值能够达到最优(0.4)。
- 在r值根据电感器最大直流电流Idc设置为0.4后,ΔI =ΔV*Δt/L就固定了,其并不会随负载电流Io的变化而变化,所以当负载Io减小后,响应的实际工作中的r值就会变大;例如最大工作电流Idc = 10A,r值为0.4,那么ΔI = 4A,当Idc下降到2A时,r = 2,此时对于非同步拓扑开关电源来说,即将进入断续导通模式(断续导通模式的计算方程更复杂),电源拓扑的很多特性将发生变化。如果要需要将开关电源(非同步拓扑)一直工作在连续导通模式,那么需要在负载电流Io最小时,保持开关电源工作在连续导通模式下,需要将电流纹波率r设置的更低。即:Io*r/2 = Io_min,可得r = 2*Io_min/Io_max,在上面的“栗子”的中,假设最小负载电流是5A,那么r =2*5/10 = 0.3。
——同步电源拓扑由于下管MOS管允许反向导通,不会进入断续导通模式,所以它允许r>2,甚至可以更大,此时进入强迫连续导通模式;但它与普通的连续导通模式有所区别:如之前所述,进入强迫连续导通模式后电感器中的电流会反向,能量将从低压传输至高压,这其实是降压拓扑中的升压模式;但传统连续导通模式下的所有基本设计方程同样适用于强迫连续导通模式。
——根据电流纹波率公式r = Von*D/(Idc*L*f)可得,除了减小负载(减小Idc)让开关电源拓扑工作在断续导通模式之外,还有两种方法:1,选择小电感值(减小L,即:增加ΔI值);2,增加输入电压(增加Von)。
- 电流纹波率r的减小会导致电感器尺寸的增加,那么r>0.4呢?输出纹波电流大小更大,除了EMI辐射之外,还带来了纹波电压的上升和滤波电容损耗的增加;但目前使用的大容量陶瓷电容器和聚合物电容器(其特性具体参考:《电容器分类》)的ESR非常小(ΔV= ΔI*ESR,纹波电压很小),可以容许流过电容器的电流也非常大(铝电解电容一般容许几A的浪涌电流),不存在纹波电流大导致的过热老化问题,所以增加r值:未必会使电容器所占空间增大,但可以显著减小电感器尺寸。
——所以可以设置r的值在0.6~1之间,使得开关电源的性能更好,同时电感器尺寸还可以减小30%~50%。
4.最“恶劣”输入电压
关于最“恶劣”电压的分析,我们在《正激和反激开关电源拓扑》中参数的设计中已经有所涉及,只是当时没有系统的来阐述这个问题。在实际工作中,输入电压是有一个范围的,举个栗子:外部电源提供+12V电源,其波动范围是20%,转化成电压范围就是9.6V~14.4V。那么我们需要对输入电源电压变化时电感器的交流电流、直流电流和峰值电流是如何变化的,其中最重要的是考虑:输入电压在多大时,峰值电流最大;即,定义电感器峰值电流最大时的输入电压为最“恶劣”输入电压。对于电感器来说,需要按照这个最“恶劣”输入电压来设计。
——对于开关管和二极管来说,还需考虑在多大输入电压下的最大电压压力,需要保证开关管和二极管在最大电压压力下不被损坏;最大电压压力可以根据对开关管导通和关断的分析来获得。
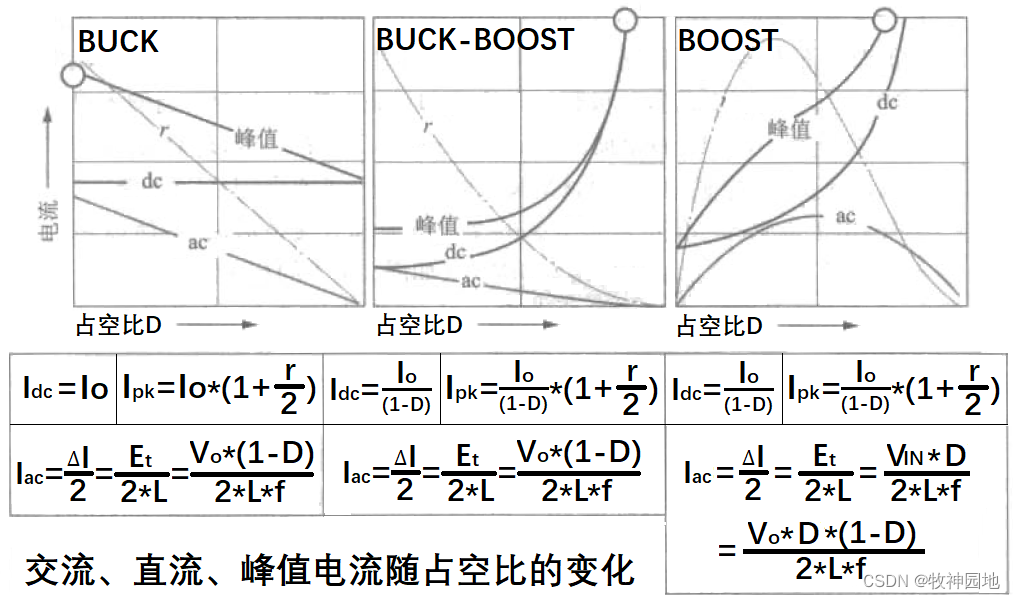
如下图所示,为三种拓扑的电感电流(直流电流、交流电流和峰值电流)和电流纹波率r随占空比(输入电压)的变化,如下以BUCK和BUCK-BOOST拓扑为例进行分析。
——输入电压与占空比的关系,我们上面已有说明:高占空比对应低输入电压,低占空比对应高输入电压;对所有拓扑有效。
- BUCK拓扑:
- 当输入电压增加时,占空比减小,由于ΔI = Voff*Toff/L,可得ΔI/Toff = Voff/L = Vo/L(BUCK拓扑的Toff时电感器两端电压为输出电压Vo,保持不变),所以Toff阶段电流变化斜率ΔI/Toff保持不变;由于占空比减小(Ton/T值减小),Toff时间随占空比线性增加,所以ΔI线性增加;如上左图所示,电感交流电流Iac随占空比的增加而线性减小;
- 在BUCK拓扑中,电感直流电流Idc等于负载电流Io,所以在负载电流Io不变时,电感直流电流Idc也不变;
- 电感峰值电流Ipk = Idc+Iac,Idc保持不变,而Iac随占空比的增加而线性减小,所以电感峰值电流Ipk也随占空比的增加而线性减小;
——BUCK拓扑的电感器峰值电流Ipk最大值:在占空比最小处,即输入电压最大处(输入与输出电压压差最大)。
- 电流纹波率r = ΔI/Idc = 2*Iac/Idc,与Iac成正比而与Idc成反比,同理Idc保持不变,而I
 ac随占空比的增加而线性减小,所以电流纹波率r随占空比的增加而线性减小。
ac随占空比的增加而线性减小,所以电流纹波率r随占空比的增加而线性减小。
- BUCK-BOOST拓扑:
- 当输入电压增加时,占空比减小,由于ΔI = Voff*Toff/L,可得ΔI/Toff = Voff/L = Vo/L(BUCK-BOOST拓扑的Toff时电感器两端电压为输出电压Vo,保持不变),所以Toff阶段电流变化斜率ΔI/Toff保持不变;由于占空比减小(Ton/T值减小),Toff时间随占空比线性增加,所以ΔI线性增加;如上中图所示,电感交流电流Iac随占空比的增加而线性减小;
- 在BUCK-BOOST拓扑中,电感直流电流Idc = Io/(1-D),负载电流Io不变而占空比增加,此时Idc随占空比的增加而指数增加;
- 电感峰值电流Ipk = Idc+Iac,Idc随占空比增加指数增加,而Iac随占空比的增加而线性减小,所以综合起来:电感峰值电流I
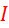 pk也随占空比的增加(输入电压的减小)而指数增加;
pk也随占空比的增加(输入电压的减小)而指数增加;
——BOOST拓扑的电感器峰值电流I![]() pk最大值:在占空比最大处,即输入电压最小处(输入与输出电压压差最大)。
pk最大值:在占空比最大处,即输入电压最小处(输入与输出电压压差最大)。
- 电流纹波率r =ΔI/Idc = 2*Iac/Idc,与Iac成正比而与Idc成反比,同理Idc随占空比的增加而指数增加,而Iac随占空比的增加而线性减小,所以综合起来:电流纹波率r随占空比的增加而指数减小。
- BOOST拓扑:
- 当输入电压增加时,占空比减小,由于ΔI = Von*Ton/L = (Vin/L)*[(Vo-Vin)/Vo]*T = Vin*(Vo-Vin)/(L*Vo)*T,当Vin从0增加值Vo,其曲线如上右图所示,其Iac最大值为Vin = Vo/2时(D=0.5);
- 在BOOST拓扑中,电感直流电流Idc = Io/(1-D),负载电流Io不变而占空比增加,此时Idc随占空比的增加而指数增加(如BUCK-BOOST拓扑);
- 电感峰值电流Ipk = Idc+Iac,I
 dc随占空比增加指数增加,而Iac随占空比的增加而先增加后减小(D=0.5为界),所以综合起来:电感峰值电流I
dc随占空比增加指数增加,而Iac随占空比的增加而先增加后减小(D=0.5为界),所以综合起来:电感峰值电流I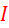 pk也随占空比的增加(输入电压减小)而指数增加;
pk也随占空比的增加(输入电压减小)而指数增加;
——BOOST拓扑的电感器峰值电流I![]() pk最大值:在占空比最大处,即输入电压最小处(输入与输出电压幅值压差最大)。
pk最大值:在占空比最大处,即输入电压最小处(输入与输出电压幅值压差最大)。
- 电流纹波率r =ΔI/Idc = 2*Iac/Idc,与Iac成正比而与Idc成反比,同理Idc随占空比的增加而指数增加,而Iac随占空比的增加而先增加后减小(D=0.5为界),在Vin =0和Vin=Vo时Iac = 0,所以如上右图所示,综合起来:电流纹波率r随占空比的增加而先增加后减小(起点和终点都为0)。
- 我们可以总结得到如下结论:
- BUCK电源要在最大输入电压(Vinmax,即Dmin)条件下,设计BUCK电源电路;
- BUCK-BOOST电源要在最小输入电压(Vinmin,即Dmax)条件下,设计BUCK-BOOST电源电路;
- BOOST电源要在最小输入电压(Vinmin,即Dmax)条件下,设计BOOST电源电路。
这篇关于开关电源基础05:基本开关电源电感器设计(1)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




