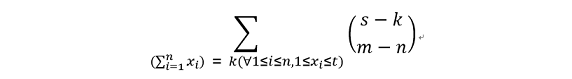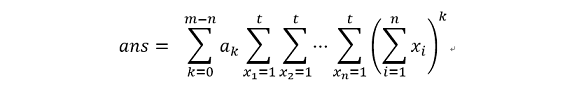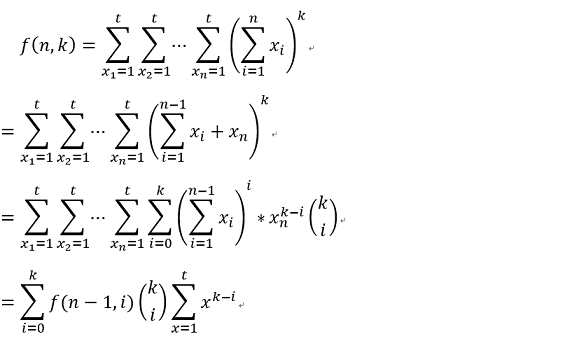WC模拟（1.14） T2 Everyone will meet some difficult

本文主要是介绍WC模拟（1.14） T2 Everyone will meet some difficult，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Everyone will meet some difficult

题目背景：

1.14 WC模拟T2  

分析：数学 + 数论

 

100分做法我不会，也不想去学，所以就说一下80分做法吧，首先，我们可以知道答案是

显然，对于一个固定的k，组合数是一个m - n次多项式，并且对于任意k，这个多项式的系数显然都是相同的，那么我们定义，k的i次项系数为a_k，那么显然：

显然对于a_i，我们可以直接爆拆组合数在(m - n)²的时间搞定。

所以直接考虑后面部分，令：

直接用矩阵快速幂优化一下上面的递推式就可以了。

时间复杂度O((m - n)³log(m- n))。

Source:

/*created by scarlyw
*/
#include <cstdio>
#include <string>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
#include <cctype>
#include <vector>
#include <set>
#include <queue>
#include <ctime>
#include <bitset>inline char read() {static const int IN_LEN = 1024 * 1024;static char buf[IN_LEN], *s, *t;if (s == t) {t = (s = buf) + fread(buf, 1, IN_LEN, stdin);if (s == t) return -1;}return *s++;
}/*
template<class T>
inline void R(T &x) {static char c;static bool iosig;for (c = read(), iosig = false; !isdigit(c); c = read()) {if (c == -1) return ;if (c == '-') iosig = true;	}for (x = 0; isdigit(c); c = read()) x = ((x << 2) + x << 1) + (c ^ '0');if (iosig) x = -x;
}
//*/const int OUT_LEN = 1024 * 1024;
char obuf[OUT_LEN], *oh = obuf;
inline void write_char(char c) {if (oh == obuf + OUT_LEN) fwrite(obuf, 1, OUT_LEN, stdout), oh = obuf;*oh++ = c;
}template<class T>
inline void W(T x) {static int buf[30], cnt;if (x == 0) write_char('0');else {if (x < 0) write_char('-'), x = -x;for (cnt = 0; x; x /= 10) buf[++cnt] = x % 10 + 48;while (cnt) write_char(buf[cnt--]);}
}inline void flush() {fwrite(obuf, 1, oh - obuf, stdout);
}///*
template<class T>
inline void R(T &x) {static char c;static bool iosig;for (c = getchar(), iosig = false; !isdigit(c); c = getchar())if (c == '-') iosig = true;	for (x = 0; isdigit(c); c = getchar()) x = ((x << 2) + x << 1) + (c ^ '0');if (iosig) x = -x;
}
//*/const int MAXN = 1000000 + 10;
const int mod = 1000000000 + 7;long long fac[MAXN], inv_fac[MAXN];
long long s, t, n, m;inline long long mod_pow(long long a, long long b) {int ans = 1;for (; b; b >>= 1, a = a * a % mod)if (b & 1) ans = ans * a % mod;return ans;
}inline void get_c() {fac[0] = 1;for (int i = 1; i < MAXN; ++i) fac[i] = fac[i - 1] * i % mod;inv_fac[MAXN - 1] = mod_pow(fac[MAXN - 1], mod - 2);for (int i = MAXN - 2; i >= 0; --i) inv_fac[i] = inv_fac[i + 1] * (i + 1) % mod;
}inline long long c(int n, int m) {if (n < m) return 0;return fac[n] * inv_fac[m] % mod * inv_fac[n - m] % mod; 
}inline void solve_1() {get_c();long long ans = 0;for (int i = 0, sign = 1; i <= n; ++i, sign = -sign) {ans = (((ans + (long long)sign * c(n, i) * c(s - i * t, m)) % mod) + mod) % mod;}std::cout << ans;
}const int MAXD = 100 + 10;struct matrix {int n;long long a[MAXD][MAXD];matrix(int n = 0) : n(n) {for (int i = 0; i <= n; ++i)for (int j = 0; j <= n; ++j)a[i][j] = 0;}inline matrix operator * (const matrix &c) const {matrix ret(n);for (int i = 0; i <= n; ++i)for (int k = 0; k <= n; ++k)for (int j = 0; j <= n; ++j)ret.a[i][j] += a[i][k] * c.a[k][j] % mod;for (int i = 0; i <= n; ++i)for (int j = 0; j <= n; ++j)ret.a[i][j] %= mod;return ret;}inline matrix operator ^ (int b) const {matrix ans(n), a = *this;for (int i = 0; i <= n; ++i) ans.a[i][i] = 1;for (; b; b >>= 1, a = a * a)if (b & 1) ans = ans * a;return ans;}
} ;long long last[MAXD], cur[MAXD], sum[MAXD], mul[MAXN];
inline void solve_2() {long long ans = 0;last[0] = 1, get_c(), s %= mod;for (int i = 0; i < m - n; ++i) {for (int j = 0; j <= i + 1; ++j) cur[j] = 0;for (int j = 0; j <= i; ++j) cur[j + 1] = last[j];for (int j = 0; j <= i; ++j) cur[j] = (cur[j] + last[j] * (s - i) % mod) % mod;for (int j = 0; j <= i + 1; ++j) last[j] = cur[j];}long long ret = 1;for (int i = 1; i <= m - n; ++i) ret = ret * i % mod;ret = mod_pow(ret, mod - 2);for (int i = 0; i <= m - n; ++i) cur[i] = cur[i] * ret % mod;for (int i = 1; i <= t; ++i) mul[i] = 1;sum[0] = t;for (int i = 1; i <= m - n; ++i) {for (int j = 1; j <= t; ++j)mul[j] = mul[j] * j % mod, sum[i] += mul[j];sum[i] %= mod;}matrix move(m - n);for (int i = 0; i <= m - n; ++i)for (int j = 0; j <= m - n; ++j)move.a[i][j] = c(j, i) * sum[j - i] % mod;move = (move ^ n);
//	for (int i = 0; i <= m - n; ++i, std::cout << '\n')
//		for (int j = 0; j <= m - n; ++j)
//			std::cout << move.a[i][j] << " ";for (int i = 0, sign = 1; i <= m - n; ++i, sign = -sign)ans += (long long)sign * cur[i] * move.a[0][i] % mod;ans = (ans % mod + mod) % mod;std::cout << ans;
}int main() {freopen("success.in", "r", stdin);freopen("success.out", "w", stdout);R(s), R(t), R(n), R(m);if (s < MAXN && m < MAXN) solve_1();else solve_2();return 0;
}

这篇关于WC模拟（1.14） T2 Everyone will meet some difficult的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---