基于蜜獾算法的函数寻优算法

一、理论基础

蜜獾算法(HBA)模拟了蜜獾的觅食行为。为了找到食物源，蜜獾要么嗅、挖，要么跟随蜜獾。第一种行为为挖掘模式，而第二种行为为采蜜模式。在挖掘模式中，它利用自己的嗅觉来确定猎物的大致位置；当到达那里时，它会绕着猎物移动，以选择合适的位置来挖掘和捕捉猎物。在采蜜模式中，蜜獾利用引导獾的位置直接定位蜂巢。

1、蜜獾算法

1.1 初始化阶段

根据式(1)初始化蜜獾的数量(种群规模)和个体的位置：$$x_i=l{b}_i+r_1\times (u{b}_i-l{b}_i)\text{\hspace{1em}(1)}$$其中，$r_1$为$(0,1)$内的随机数；$x_i$为$N$个候选个体的第$i$个个体的位置；$l{b}_i$和$u{b}_i$分别为搜索空间的下界和上界。

1.2 定义强度$I$

强度和猎物的集中力以及和蜜獾之间的距离有关。$I_i$是猎物的气味强度；如果气味高，则运动速度快，反之亦然。如式(2)计算所示：$$\begin{array}{rl}& I_i=r_2\times \frac{S}{4\pi d_i^2}\\ & S=(x_i-x_{i+1}{)}^2\\ & d_i=x_{prey}-x_i\end{array}\text{\hspace{1em}(2)}$$其中，$S$是源强度或集中强度；$d_i$表示猎物与当前蜜獾个体的距离。

1.3 更新密度因子

密度因子$\alpha$控制时变随机化，以确保从勘探到开采的平稳过渡。使用式(3)更新随迭代次数减少的递减因子$\alpha$，以随时间减少随机化。$$\alpha =C\times \exp \left(\frac{-t}{t_{\max }}\right)\text{\hspace{1em}(3)}$$其中，$t_{\max }$为最大迭代次数；$C$是一个大于等于1的常数(默认为2)。

1.4 跳出局部最优

这一步和接下来的两步用于跳出局部最优区域。在这种情况下，所提出的算法使用了一个改变搜索方向的标志$F$，以利用大量机会让搜索个体严格扫描搜索空间。

1.5 更新个体位置

如前所述，HBA位置更新过程($x_{new}$)分为两个部分，即“挖掘阶段”和“采蜜阶段”。下面给出解释：

1.5.1 挖掘阶段

在挖掘阶段，蜜獾执行类似于心脏线形状的动作。心形运动可通过式(4)进行模拟：$$x_{new}=x_{prey}+F\times \beta \times I\times x_{prey}+F\times r_3\times \alpha \times d_i\times |\cos (2\pi r_4)\times [1-\cos (2\pi r_5)]|\text{\hspace{1em}(4)}$$其中，$x_{prey}$是到目前为止全局最优位置；$\beta \ge 1$(默认为6)是蜜獾获取食物的能力；$d_i$为猎物与当前蜜獾个体的距离，见式(2)；$r_3$、$r_4$和$r_5$是$(0,1)$之间的三个不同的随机数；$F$为改变搜索方向的标志，使用式(5)确定：$$F=\{\begin{array}{l}1\text{if}{r}_6\le 0.5\\ -1\text{else}\end{array}\text{\hspace{1em}(5)}$$在挖掘阶段，蜜獾严重依赖于猎物的气味强度、与猎物之间的距离以及时变搜索影响因子$\alpha$。此外，在挖掘活动中，獾可能会受到任何干扰，从而使其无法找到更好的猎物位置。

1.5.2 采蜜阶段

蜂蜜獾跟随蜂蜜向导獾到达蜂巢的情况可模拟为式(6)：$$x_{new}=x_{prey}+F\times r_7\times \alpha \times d_i\text{\hspace{1em}(6)}$$其中，$x_{new}$为更新后的蜜獾个体位置；$x_{prey}$为猎物位置；$F$和$\alpha$分别由式(5)和式(3)确定；$r_7$为$(0,1)$之间的随机数。从式(6)可以观察到，根据距离信息$d_i$，蜜獾在猎物位置$x_{prey}$附近进行搜索。在这一阶段，搜索受到随迭代变化的搜索行为$\alpha$的影响。此外，一只蜜獾可能会受到$F$干扰。

2、算法伪代码

HBA算法伪代码如图1所示。

二、仿真实验与分析

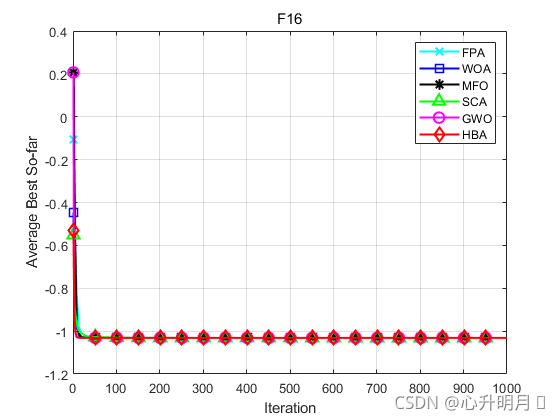
以常用23个测试函数中的F1、F2(单峰函数/30维)、F9、F10(多峰函数/30维)、F16、F17(固定维度的多峰函数/2维)为例，将HBA算法分别与花授粉算法(FPA)、鲸鱼优化算法(WOA)、飞蛾火焰优化算法(MFO)、正弦余弦算法(SCA)以及灰狼优化算法(GWO)进行对比，设置种群规模为30，最大迭代次数为1000，每个算法独立运行30次。
结果显示如下：

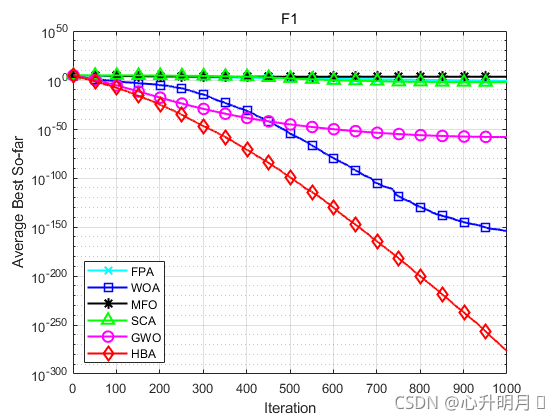
函数：F1
FPA：最差值: 0.45312,最优值:0.059663,平均值:0.1572,标准差:0.078226
WOA：最差值: 3.8468e-153,最优值:1.787e-166,平均值:1.586e-154,标准差:7.0824e-154
MFO：最差值: 20000,最优值:2.7671e-05,平均值:2000.0023,标准差:4842.341
SCA：最差值: 0.083351,最优值:6.3116e-09,平均值:0.0063474,标准差:0.015506
GWO：最差值: 1.1638e-57,最优值:1.9593e-62,平均值:6.8682e-59,标准差:2.1017e-58
HBA：最差值: 4.9384e-276,最优值:1.0454e-286,平均值:2.4754e-277,标准差:0
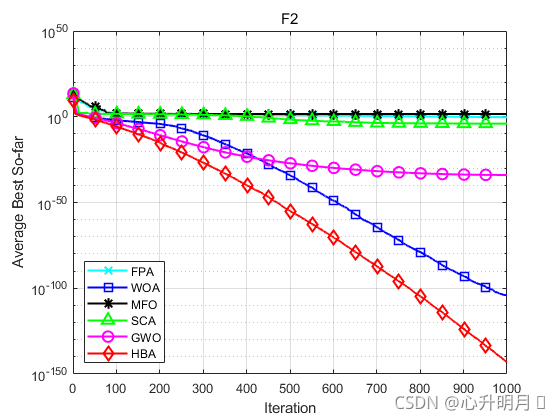
函数：F2
FPA：最差值: 1.1249,最优值:0.2083,平均值:0.50268,标准差:0.18398
WOA：最差值: 2.6492e-103,最优值:1.9096e-112,平均值:1.0355e-104,标准差:4.8313e-104
MFO：最差值: 90,最优值:0.00069882,平均值:37.3337,标准差:23.9151
SCA：最差值: 0.002434,最优值:3.5521e-08,平均值:9.9781e-05,标准差:0.00044213
GWO：最差值: 3.9706e-34,最优值:2.1175e-35,平均值:1.1445e-34,标准差:1.0969e-34
HBA：最差值: 2.715e-142,最优值:4.052e-151,平均值:9.0628e-144,标准差:4.9566e-143
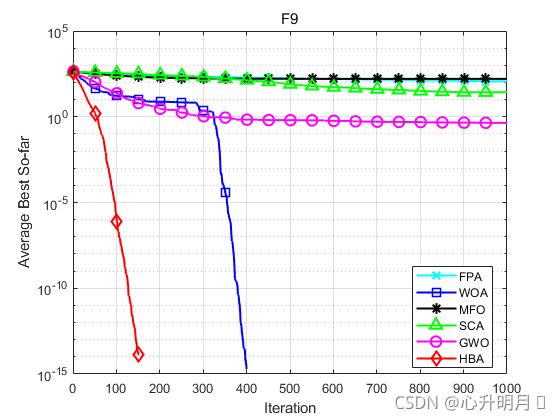
函数：F9
FPA：最差值: 139.1564,最优值:91.7519,平均值:115.611,标准差:11.7281
WOA：最差值: 0,最优值:0,平均值:0,标准差:0
MFO：最差值: 236.1595,最优值:85.5661,平均值:162.5257,标准差:35.7019
SCA：最差值: 128.5608,最优值:4.0412e-05,平均值:26.6363,标准差:35.3467
GWO：最差值: 6.3307,最优值:0,平均值:0.4363,标准差:1.4463
HBA：最差值: 0,最优值:0,平均值:0,标准差:0
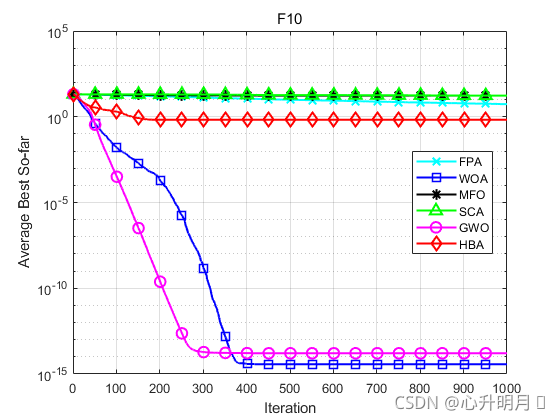
函数：F10
FPA：最差值: 13.6963,最优值:0.36228,平均值:5.4049,标准差:3.7088
WOA：最差值: 7.9936e-15,最优值:8.8818e-16,平均值:3.7303e-15,标准差:1.9571e-15
MFO：最差值: 19.964,最优值:1.5018,平均值:16.9922,标准差:5.3634
SCA：最差值: 20.3051,最优值:0.00051109,平均值:17.0372,标准差:6.5228
GWO：最差值: 2.2204e-14,最优值:1.1546e-14,平均值:1.6165e-14,标准差:2.9724e-15
HBA：最差值: 19.9418,最优值:8.8818e-16,平均值:0.66473,标准差:3.6409
函数：F16
FPA：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:6.2532e-16
WOA：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:1.7865e-11
MFO：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:6.7752e-16
SCA：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:1.9964e-05
GWO：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:6.8281e-09
HBA：最差值: -1.0316,最优值:-1.0316,平均值:-1.0316,标准差:6.2532e-16
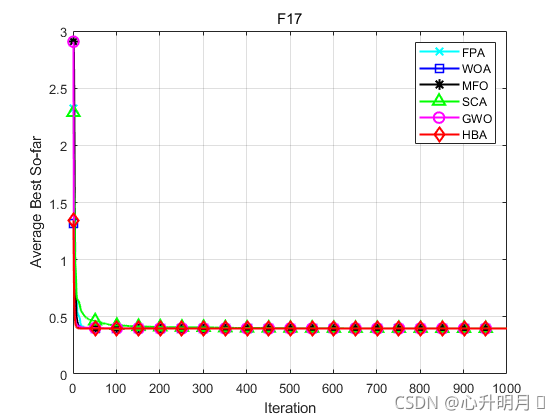
函数：F17
FPA：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0
WOA：最差值: 0.3979,最优值:0.39789,平均值:0.39789,标准差:2.0598e-06
MFO：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0
SCA：最差值: 0.40065,最优值:0.39791,平均值:0.39864,标准差:0.00065531
GWO：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:1.9543e-07
HBA：最差值: 0.39789,最优值:0.39789,平均值:0.39789,标准差:0

结果表明，HBA算法具有更快的收敛速度、更高的收敛精度以及更好的寻优能力。

三、参考文献

[1] Fatma A. Hashim, Essam H. Houssein, Kashif Hussain, et al. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems[J]. Mathematics and Computers in Simulation, 2021: 84-110.