算法竞赛入门【码蹄集进阶塔335题】(MT2276-2280）

算法竞赛入门【码蹄集进阶塔335题】(MT2276-2280）

前言

为什么突然想学算法了？

> 用较为“官方”的语言讲，是因为算法对计算机科学的所有分支都非常重要。 在绝大多数的计算机科学分支领域中，要想完成任何实质性的工作，理解算法的基础知识并掌握与算法密切相关的数据结构知识是必不可少的。
> 但从实际而言，是因为当下快到了考研和找工作的年纪(ಥ_ಥ)，无论走哪一条路，都不免需要一些相对丰富的算法知识，是故，便产生了一个暑假速成算法的计划，可能对于像我这种算法竞赛小白而言，几乎很难，但我仍然还是想尝试一下，毕竟，梦想还是要有的，万一实现了呢？～(￣▽￣～)~

为什么选择码蹄集作为刷题软件？

码蹄集，是在全国高等学校计算机教学与产业实践资源建设专家委员会(TIPCC) 指导下建设的，其依托全国各大名校计算机系和清华大学出版社等单位的强大资源，旨在为计算机学习爱好者提供全面和权威的计算机习题。

目录

1. MT2276 数的自我

（1）题目描述
提瓦特大陆上有一个贫穷的占星术士小码哥，出于占星术的要求，他时常要解决一些困难的数学问题。这天，上天给了他一个启示:有一类称作 Self一Numbers的数。对于每一个正整数n，我们定义d(n)为n加上它每一位数字的和。例如，d(75)= 75＋7＋5=87。给定任意正整数n作为一个起点，都能构造出一个无限递增的序列: n,d(n), d(d(n)), d(d(d(n))),…例如，如果你从33开始，下一个数是33+3+3=39，再下一个为39+3+9=51，再再下一个为51+5+1=57，因此你所产生的序列就像这样:33,39,51,57,69，84,96,111,114,120,123,129,141,…数字n被称作d(n)的发生器。在上面的这个序列中，33是39的发生器，39是51的发生器，51是57的发生器等等。有一些数有超过一个发生器，如101的发生器可以是91和100。一个没有发生器的数被称作Self 一Number。如前13个 Self - Number为1，3，5,7，9，20，31,42,53,64,75,86,97。我们将第i个Self -Number表示为a[i]，所以a[1]= 1,a[2]= 3,a[3]=5…

现在小码哥需要找到一个[1,N]的区间内所有的Self - Number，请你帮帮他。

格式

输入格式:
第一行输入以空格隔开的两个整数Ⅳ和K，第二行输入K个以空格隔开的整数$1,82,s3 . . . Sk 。
.
输出格式:
第一行你需要输出一个数，这个数表示在闭区间[1,N]中Self - Number的数量。
第二行必须包含以空格分隔的K个数，表示a[s1] …a[sk]，这里保证所有的a[s1] …a[sg.]都小于N。(例如，如果N=100，s:可以为1-13，但不能为14，因为a[14]=108 > 100）。

样例1

输入:
100 10
1 2 3 4 5 6 7 11 12 13
.
输出:
13
1 3 5 7 9 20 31 75 86 97

备注：

其中:1<N ≤107,1<K ≤5000。

（2）参考代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int cnt,n,k;
int ans[1000010];
bool flag[10000010];
int next(int num){int ans=0;ans+=num;while(num!=0){ans+=num%10;num/=10;}return ans;
}
int main(){memset(flag,true,sizeof(flag));scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)if(flag[i]){ans[++cnt]=i;int now=next(i);while(now<=n&&flag[now]) {flag[now]=false;now=next(now);}}printf("%d\n",cnt);int t=0;for(int i=1;i<=k;i++){scanf("%d",&t);printf("%d ",ans[t]);}
}

2. MT2277 分数个数

（1）题目描述

定义简分数为，分母d >分子n，且不可以再约分。

如果我们把d≤6的所有简分数以从小到大的顺序排列，则有:
1/6,1/5,1/4,1/3,2/5,1/2,3/5,2/3,3/4,4/5,5/6，可以看到这个集合中包含的分数有11个。给定d，求这个最简分数集合中包含有多少个分数?

格式

输入格式: 一个整数d。
.
输出格式: 输出一个整数表示包含的分数的个数。

样例1

输入: 6
.
输出: 11

备注：

提示:2<d≤105。

（2）参考代码

#include<bits/stdc++.h>
using namespace std;int main()
{long long n,i,k,ans,t,sum;scanf("%lld",&n);sum=0;for(k=2;k<=n;k++){ans=k;t=k;for(i=2;i*i<=t;i++){if(t%i==0){ans-=ans/i;while(t%i==0) t/=i;}}if(t!=1) ans -= ans/t;sum+=ans;}printf("%lld\n",sum);return 0; return 0;
}

3. MT2278 欧拉函数

（1）题目描述
给出给定正整数n，求f(n)，此处f(n)定义为小于n的所有与n互素的数的个数。

格式

输入格式: 一个整数n 。
.
输出格式: 输出一行一个整数表示答案。

样例1

输入格式: 4
.
输出格式: 2

备注：

其中:2≤n ≤1e9。

（2）参考代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL maxa = 1e10 + 10;
LL euler_deall(LL n)
{LL res = n;for (LL i = 2; i * i <= n; i++){if (n % i == 0){res = res / i * (i - 1);for (; n % i == 0; n /= i);}}if (n != 1)res = res / n * (n - 1);return res;
}
int main()
{LL n;scanf("%lld", &n);printf("%lld\n", euler_deall(n));
}

4. MT2279 欧拉函数2

（1）题目描述

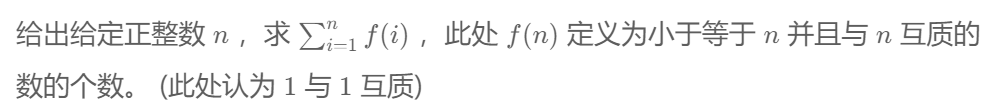
格式

输入格式: 一个正整数n。
.
输出格式: 输出一行一个整数表示答案。

样例1：

输入： 4
.
输出：6

备注：

其中: 1≤n ≤ 1e6

（2）参考代码

def main():n = int(input())primes = [] # 存质数values = [1] * (n + 1) # 存欧拉函数的值values[0] = 0 # 0的欧拉函数值为0st = [True for _ in range(n + 1)] # 存每个数是否是质数for i in range(2, n + 1):  # 对于每个大于2的自然数if st[i]:  # 如果是质数，加入质数列表，质数的欧拉函数值为i-1primes.append(i)values[i] = i - 1for p in primes:if p > n / i: breakst[p * i] = False  # p*i不是质数，设置为False# 如果i % p != 0 p不是i的质因数，则eulor(p*i) = p * eulor(i) * (p-1) / p = (p-1)* eulor(i)values[p * i] = (p - 1) * values[i]if i % p == 0:# 如果i % p = 0， p是i的质因数，则eulor(p*i) = p * eulor(i)values[p * i] = p * values[i]breakprint(sum(values))if __name__ == '__main__':main();

5. MT2280 数字游戏

（1）题目描述

格式

输入格式: 输入只有一行两个整数，分别代表宗教数m 和房间数n。
.
输出格式: 输出一行一个整数代表答案。

样例1

输入格式: 2 3
.
输出格式: 6

备注：

其中: 1≤m ≤le8,1 ≤n ≤1e10

（2）参考代码

#include<bits/stdc++.h> 
/*
思路：不越狱的状态好计算所以：越狱数=总的状态数-不越狱的状态数
其中 总的状态数为：m^n不越狱的状态数： m*（m-1）^(n-1) :只有第一个可以选择m个宗教，其他的只能选和前一个不同的宗教所以是m-1种情况
这里计算用了快速幂的方法。
*/
using namespace std;
long long p=1007;
long long qpow(long long x, long long y){if(y==0)return 1;if(y%2==1){return qpow(x, y - 1) * x % p;}else{long long t = qpow(x, y/2) % p;return t*t % p;}
}
int main( )
{long long m,n;cin>>m>>n;long long ans = qpow(m,n)-(m*qpow(m-1,n-1)%p);cout<<(ans+p)%p<<endl;//注意需要+p之后再取 %p，防止有负数return 0;
}

结语

感谢大家一直以来的不断支持与鼓励，码题集题库中的进阶塔350题正在逐步更新，之后会逐步跟进星耀，王者的题，尽请期待！！！
同时，也希望这些题能帮助到大家，一起进步，祝愿每一个算法道路上的“苦行僧”们，都能够历经磨难，终成正果，既然选择了这条路，走到了这里，中途放弃，岂不是太过可惜？

另附中国计算机学会的杰出会员、常务理事轩哥博士的B站视频讲解链接https://space.bilibili.com/518554541/?spm_id_from=333.999.0.0，供大家更好的进行学习与刷题～(￣▽￣～)~

愿你的结局，配得上你一路的颠沛流离。