算法通过村第十八关-回溯|青铜笔记|什么叫回溯（后篇）

本文主要是介绍算法通过村第十八关-回溯|青铜笔记|什么叫回溯（后篇），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

前言
回溯热身问题
- 输出二叉树的所有路径：
- 路径总和问题：
总结

前言

提示：今夜思量千条路，明朝依旧卖豆腐。 --谚语

回溯是非常重要的算法思想之一，主要解决一些暴力枚举也搞不定的问题（这里埋个坑💣）例如组合、分割、子集、棋盘等等。从性能角度来看回溯算法的效率并不是很高，但是对于暴力也解决不了的问题，它往往很快可以出结果，效率低就可以理解了吧。接下来，就看看回溯的事情吧🤩

回溯热身问题

输出二叉树的所有路径：

参考题目地址：257. 二叉树的所有路径 - 力扣（LeetCode）

在这里插入图片描述

我们可以注意看这里有几个叶子节点，就有几条路径，那么怎么找叶子节点呢？我们知道深度优先搜索就是从根节点开始一直找到叶子结点，我们这里可以先判断当前节点是不是叶子节点，在决定是不是向下走，如果走到叶子节点，我们就加一条路径。

这里从回溯的角度看问题，达到第一条路径后，怎么得到第二条路径呢？当然很明显需要撤销一下上一个点对吧！我们继续看递归：

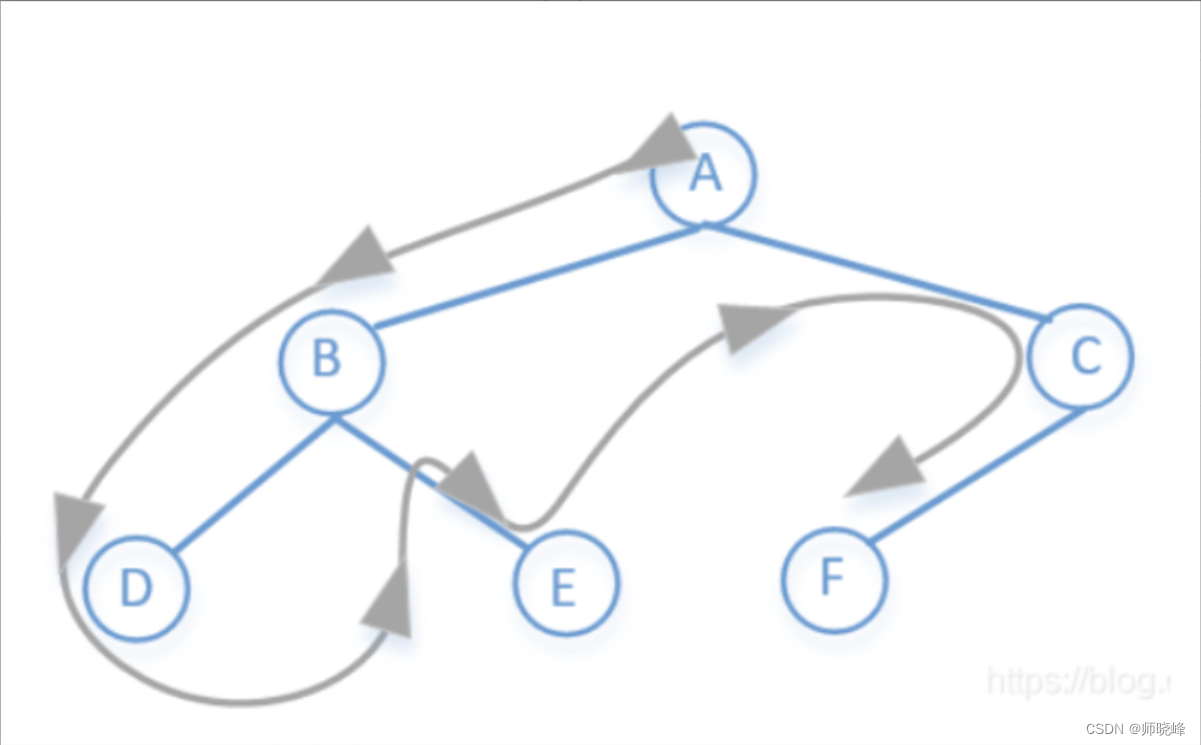
在这里插入图片描述
完整代码：（回溯操作）

 public List<String> binaryTreePaths(TreeNode root) {List<String> ans = new ArrayList<String>();dfs(root,new ArrayList(),ans);return ans; }public static void dfs(TreeNode root, List<Integer> path,List<String> ans){if(root == null){return;}path.add(root.val);if(root.left == null && root.right == null){ans.add(getPathToString(path));}dfs(root.left,path,ans);dfs(root.right,path,ans);path.remove(path.size() - 1);}public static String getPathToString(List<Integer> path){StringBuilder sb = new StringBuilder();sb.append(path.get(0));for(int i = 1; i < path.size(); i++){sb.append("->").append(path.get(i));}return sb.toString();}
}

路径总和问题：

参考题目地址：113. 路径总和 II - 力扣（LeetCode）

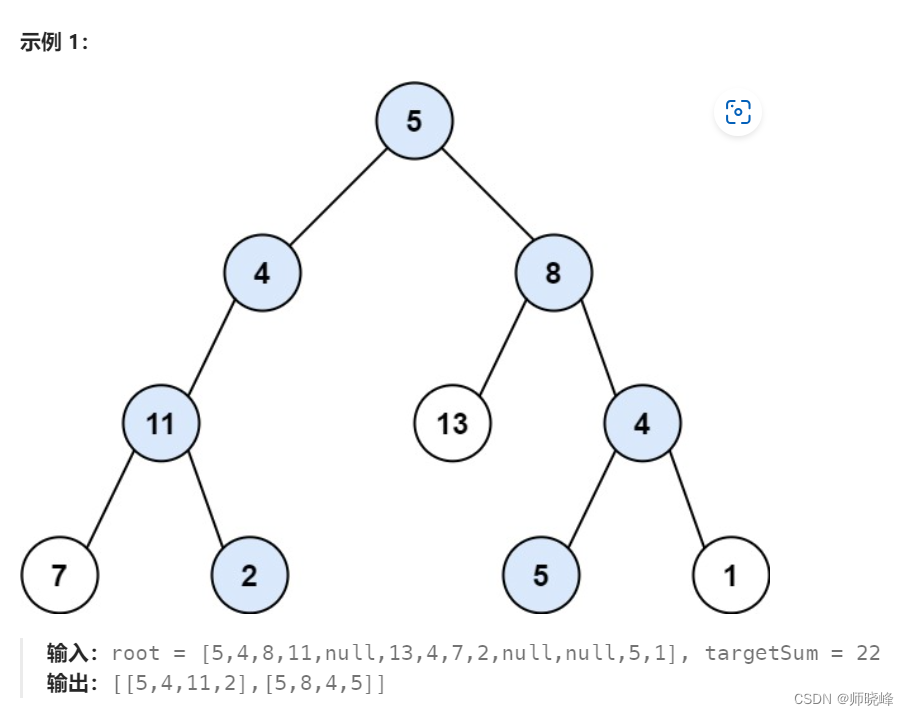
在这里插入图片描述

本题需要怎么做呢？从上面的题目种，我们也有灵感，这里找的目标值是22，根节点的值是5，也就是说左右和为17.我们继续左子树，发现是4，此时我们要找的是13继续往下找左右子树。依次类推右边也是一样的。当然这里到达11时，我们就需要在往后找，目标值时2，显然这里7已经不合适了，移除7，继续访问2.

同样右边也是这样操作的，我们总和为17就完成目标了。

展示一下代码：（回溯操作)

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> res = new ArrayList<>();Deque<Integer> path = new ArrayDeque<>();dfs(root,targetSum,path,res);return res;}public void dfs(TreeNode root,int targetSum,Deque<Integer> path,List<List<Integer>> res ){if(root == null){return;}// 这里处理很关键targetSum -= root.val;path.add(root.val);// 添加一个条件if(targetSum ==0 && root.left == null && root.right == null){res.add(new LinkedList(path));}dfs(root.left,targetSum,path,res);dfs(root.right,targetSum,path,res);path.removeLast();}