本文主要是介绍离散数学实践-编程实现利用真值表法求主析取范式以及主合取范式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
*本文为博主本人校内的离散数学专业课的实践作业。由于实验步骤已经比较详细,故不再对该实验额外提供详解,本文仅提供填写的实验报告内容与代码部分,以供有需要的同学学习、参考。
--------------------------------------
编程语言:C++
编译环境:gcc 10.3.0
目录
一、实验目的
二、实验内容
三、实验步骤及实验结果
1、实验步骤
2、函数接口
3、实验源码
四、实验结果的分析与总结
一、实验目的
1.熟悉主合取范式和主析取范式的构成
2.真值表的输出和打印
3.通过二进制转换成主范式
二、实验内容
根据赋值输出真值表,主合取范式和主析取范式(编程语言不限)。
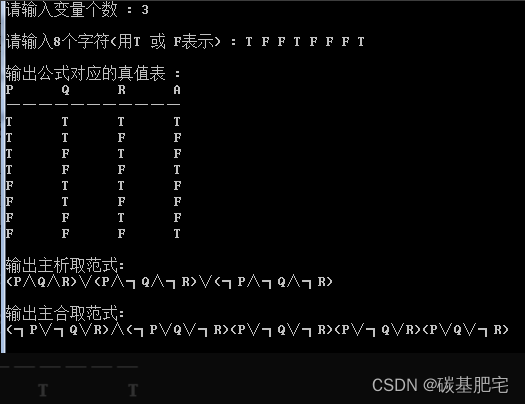
三、实验步骤及实验结果
1、实验步骤
(1)输入变量个数
在主函数中进行输入,以变量n接收。
(2)输入真值结果
在主函数中进行输入,以变长数组valueRet[totalNumber+1]接收。真值结果共2的n次方个,为了后续对真值表的操作方便,这里将数组长度定义为2的n次方+1,令操作时下标从1开始,下标为0处的元素搁置。
(3)进行真值表赋值
创建真值表数组truthTable[totalNumber+1][n+1],用于存放真值表相关信息。用0和1来表示命题变元可能的各个取值。有n个命题变元,故一共要赋值n列、2^n行次。下面以n为3来解释程序:
当n为3时也即有3个命题变元时,共有8个真值结果(要输入8次T或F)。可能的取值为0到2^3-1即0到7.将0到7这9个数转换为2进制,并将每个位分配给每个变元即可。如:
P Q R
1 1 1
0 1 1
1 0 1
0 0 1
1 1 0
0 1 0
1 0 0
0 0 0
这些就是P、Q、R所有的取值。显然,问题转换成了将0到2^n-1 的所有数转换成2进制。易得代码。
(4)打印真值表
将数组truthTable中的值与valueRet中的值按格式打印出来。
用printf函数的域宽控制%-md来对齐打印。数组中值为1,则打印T,值为0,则打印F.for循环控制。注意变长数组的传参问题。这里没法直接传,用了二级指针来调用。
(5)求主析取范式并输出
可从真值结果为真即valueRet中的值为T判断主析取范式。找到相关行,按主析取范式的格式打印出来即可。
(6)求主合取范式并输出
和主析取范式一样,找到valueRet中值为F的行,按主和区范式的格式打印即可。
2、函数接口
//计数真值结果void CountTF(char c, int* countT, int*countF)//输出真值表void OutPutTruthTable(char** truthTable, char* valueRet, int col, int row)//主析取范式void MasterDisjunction(char** truthTable, char* valueRet, int col, int row,int countT,int* count)//主合取范式void MasterConjunction(char** truthTable, char* valueRet, int col, int row,int countF,int* count)3、实验源码
#include <iostream>
#include <stdio.h>
#include <cmath>
#include <string.h>
using namespace std;/*姓名:碳基肥宅-wyd程序功能:离散数学实践作业一:输出给定结果的真值表和主析取范式、主合取范式环境:gcc 10.3.0
*///计数真值结果
void CountTF(char c, int* countT, int*countF)
{if(c == 'T'){(*countT)++;}else if(c == 'F') //考虑到空白字符等干扰{(*countF)++;}
}//输出真值表
void OutPutTruthTable(char** truthTable, char* valueRet, int col, int row)
{ char ch = 'P';for(int i = 1; i <= col; i++) //n 相当于列{printf("%-10c",ch++);if(i == col){printf("%-10c\n",'A');}}for(int i = 1; i <= col; i++){cout << "-----------" ;}cout << endl;ch = 'P'; //用P等字母代替变元for(int i = 1; i <= row; i++){for(int j = col; j >= 1; j--){if(*((int *)truthTable +i*col +j) == 1) //二级指针调用{printf("%-10c",'T');}else{printf("%-10c",'F'); }}printf("%-10c\n",valueRet[i]);}
}//主析取范式
void MasterDisjunction(char** truthTable, char* valueRet, int col, int row,int countT,int* count)
{for(int i = 1; i <= row; i++){char ch = 'P';if(valueRet[i] == 'T'){(*count)++;cout << '(';for(int j = col; j >= 1; j--){ if(*((int *)truthTable +i*col +j) == 1){cout << ch++;}else{cout << "┓" << ch++;}if(j != 1){cout << "∧";}}cout << ')';if((*count) < countT){cout << "∨";}}}
}//主合取范式
void MasterConjunction(char** truthTable, char* valueRet, int col, int row,int countF,int* count)
{for(int i = 1; i <= row; i++){char ch = 'P';if(valueRet[i] == 'F'){(*count)++;cout << '(';for(int j = col; j >= 1; j--){if(*((int *)truthTable +i*col +j) == 0){cout << ch++;}else{cout << "┓" << ch++;}if(j != 1){cout << "∨";}}cout << ')';if((*count) < row){cout << "∧";} }}
}int main()
{//1 输入变量个数int n = 0; //变量个数cout << "请输入变量个数:> ";cin >> n;cout << endl;//2 输入真值结果int totalNumber = (int)pow(2,n); //共2^n个真值结果char valueRet[totalNumber+1]; //存放输入的真值结果memset(valueRet,0,sizeof(valueRet));int countT = 0; int countF = 0; cout << "请输入"<< totalNumber << "个真值结果(有效字符为 T 和 F,以回车结束) : ";for(int i = 1; i <= totalNumber; i++) //从1开始,和后面对齐{cin >> valueRet[i];CountTF(valueRet[i], &countT, &countF);}//测试代码//cout << countT;//cout << countF;cout << endl;//3 真值表赋值int truthTable[totalNumber+1][n+1]; //真值表数组memset(truthTable, 0, sizeof(truthTable)); //初始化 int col = 0; int row = col + 1;int i = totalNumber;//真值表命题变元赋值//将0到2^n-1的所有数转换为2进制//用行标控制0到2^n-1这些数值while(i--){int truthValue = i;while(col < n){truthTable[row][++col] = truthValue % 2; //存入1或0truthValue /= 2;}row++;col = 0; //注意每一行都要从首列开始赋值}// //测试代码
// for(int k = 0; k < totalNumber; k++)
// {
// for(int j = 0; j < n; j++)
// {
// cout << truthTable[k][j] << " ";
// }
// cout << endl;
// }//4 真值表输出cout << "公式对应的真值表:> " << endl;OutPutTruthTable((char**)truthTable,valueRet,n,totalNumber);cout << endl;//5 主析取范式输出int count = 0;cout << "主析取范式:" << endl;MasterDisjunction((char**)truthTable,valueRet,n,totalNumber,countT,&count);cout << endl;//6 主合取范式输出cout << "主合取范式:" << endl;MasterConjunction((char**)truthTable,valueRet,n,totalNumber,countF,&count);cout << endl;cout << endl;cout << endl;return 0;
}
四、实验结果的分析与总结
1、经过编程,从代码的角度考虑离散数学问题,更熟练地掌握了主析取范式和主合取范式利用真值表计算的原理。
2、变长数组作函数形参时,参数无法直接传递。考虑到这个情况,采用了二级指针的方式传递数组。但要注意,数组名并不是二级指针,而是数组指针。所以在实参部分不能直接传数组名,而要先进行强制类型转换,否则无法兼容。
3、在笔算主合取范式和主析取范式时,最后还会将结果化为含mi或Mi的式子。i的下标由极小项或极大项的二进制取值之和的十进制决定。这在代码中也能体现,并且是真值表赋值的关键的步骤之一。
4、对数组下标的控制仍然需要多加注意,因为在编程时,还是因为控制失误而debug了很久。比如数组的长度,在后面赋值等操作时为了更便捷选取了下标从1 开始,但此时数组并没有a[n]这一项,导致了打印失控。经过反复debug监视,解决了这个问题,并将数组长度设置为了n+1.
5、做完实践作业,对离散数学第一章节的理解又深入了一些。
这篇关于离散数学实践-编程实现利用真值表法求主析取范式以及主合取范式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






